Kettenhomotopie – Wikipedia

Im mathematischen Teilgebiet der homologischen Algebra ist eine Kettenhomotopie eine Abstraktion des topologischen Begriffes einer Homotopie.

Es seien ${\displaystyle X}$ und ${\displaystyle Y}$ Kokettenkomplexe und ${\displaystyle f,g\colon X\to Y}$ zwei Kettenabbildungen, d. h. Systeme von Morphismen ${\displaystyle f^{k}\colon X^{k}\to Y^{k}}$, die mit den Differentialen in dem Sinne verträglich sind, dass ${\displaystyle f^{k+1}\circ d_{X}^{k}=d_{Y}^{k}\circ f^{k}}$ gilt.

Dann ist eine Kettenhomotopie ${\displaystyle D\colon f\simeq g}$ eine Folge von Morphismen ${\displaystyle D^{k}\colon X^{k}\to Y^{k-1}}$, so dass ${\displaystyle f-g=Dd+dD}$, oder ausführlicher

${\displaystyle f^{k}-g^{k}=D^{k+1}\circ d_{X}^{k}+d_{Y}^{k-1}\circ D^{k}}$ für alle ${\displaystyle k}$,

gilt.

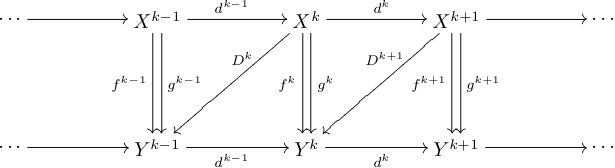
${\displaystyle f}$ und ${\displaystyle g}$ heißen homotop, wenn es eine Kettenhomotopie ${\displaystyle D\colon f\simeq g}$ gibt. Homotopie ist eine mit der Komposition verträgliche Äquivalenzrelation auf der Menge aller Kettenabbildungen.

Homotopien von Abbildungen zwischen Kettenkomplexen (und nicht Kokettenkomplexen) sind analog definiert. Zwei Kettenabbildungen ${\displaystyle f=(f_{k})_{k}}$ und ${\displaystyle g=(g_{k})_{k}}$ zwischen Kettenkomplexen ${\displaystyle X=((X_{k})_{k},(d_{k}^{X})_{k})}$ und ${\displaystyle Y=((Y_{k})_{k},(d_{k}^{Y})_{k})}$ heißen homotop, wenn es eine Folge ${\displaystyle (D_{k})_{k}}$ von Morphismen ${\displaystyle D_{k}\colon X_{k}\rightarrow Y_{k+1}}$ gibt, so dass

${\displaystyle f_{k}-g_{k}=d_{k+1}^{Y}\circ D_{k}+D_{k-1}\circ d_{k}^{X}}$ für alle ${\displaystyle k}$.^[1]

Zwei Kettenkomplexe ${\displaystyle X=((X_{k})_{k},(d_{k}^{X})_{k})}$ und ${\displaystyle Y=((Y_{k})_{k},(d_{k}^{Y})_{k})}$ heißen kettenhomotopieäquivalent, wenn es Kettenabbildungen ${\displaystyle f\colon X\rightarrow Y}$ und ${\displaystyle g\colon Y\rightarrow X}$ gibt, für die die Hintereinanderausführungen ${\displaystyle fg}$ und ${\displaystyle gf}$ jeweils homotop zur Identität sind.

• Eine Abbildung, die homotop zur Nullabbildung ist, heißt nullhomotop. Die Kategorie der Kokettenkomplexe modulo nullhomotoper Abbildungen ist die Homotopiekategorie.

• Homotope Kettenabbildungen induzieren dieselbe Abbildung in der Homologie bzw. Kohomologie.^[2]

• Ist insbesondere ${\displaystyle C}$ ein Kokettenkomplex und ${\displaystyle D\colon \mathrm {id} _{C}\simeq 0}$ eine Homotopie zwischen der Identität auf ${\displaystyle C}$ und der Nullabbildung auf ${\displaystyle C}$, so ist die Kohomologie von ${\displaystyle C}$ trivial, d. h. ${\displaystyle C}$ ist exakt. Man spricht dann auch von einer kontrahierenden Homotopie.

• Sind zwei stetige Abbildungen ${\displaystyle f}$ und ${\displaystyle g}$ zwischen topologischen Räumen ${\displaystyle X}$ und ${\displaystyle Y}$ homotop, so sind die zugeordneten Abbildungen ${\displaystyle Sf}$ und ${\displaystyle Sg}$ zwischen den zugehörigen singulären Kettenkomplexen homotop im oben definierten Sinne^[3]. Insbesondere sind die induzierten Abbildungen zwischen den singulären Homologiegruppen gleich.

• Zwei projektive Auflösungen eines Moduls über einem Ring sind homotop^[4]. Insbesondere sind die Homologien der Auflösungen gleich, was zum Begriff des abgeleiteten Funktors führt.

1. ↑ Peter Hilton und Urs Stammbach: A course in homological algebra, Springer-Verlag (1970), Graduate Texts in Mathematics, ISBN 0-387-90032-2, Kapitel IV, §3, Homotopy
2. ↑ Peter Hilton und Urs Stammbach: A course in homological algebra, Springer-Verlag (1970), Graduate Texts in Mathematics, ISBN 0-387-90032-2, Kapitel IV, §3, Satz 3.1
3. ↑ Saunders Mac Lane: Homology, Springer Grundlehren der mathematischen Wissenschaften Band 114 (1967), Theorem 8.2
4. ↑ Peter Hilton und Urs Stammbach: A course in homological algebra, Springer-Verlag (1970), Graduate Texts in Mathematics, ISBN 0-387-90032-2, Kapitel IV, §4, Satz 4.3