Kubischer Graph – Wikipedia
Ein einfacher Graph heißt in der Graphentheorie kubisch oder 3-regulär, falls alle seine Knoten den Grad 3 besitzen. Kubische Graphen sind damit reguläre Graphen. Da 1-reguläre Graphen lediglich eine Paarung darstellen und 2-reguläre Graphen in disjunkte Zyklen zerfallen, sind kubische Graphen sogesehen die einfachsten nichttrivialen Fälle regulärer Graphen.
Anzahl kubischer Graphen
[Bearbeiten | Quelltext bearbeiten]Da die Summe der Knotengrade in einfachen Graphen immer gerade sein muss, besitzen kubische Graphen immer gerade Knotenanzahl.
| n | # Zusammenhängende kubische Graphen mit n Knoten[1] | # Kubische Graphen mit n Knoten[2] |
|---|---|---|
| 2 | 0 | 0 |
| 4 | 1 | 1 |
| 6 | 2 | 2 |
| 8 | 5 | 6 |
| 10 | 19 | 21 |
| 12 | 85 | 94 |
Beispiele
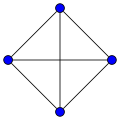
[Bearbeiten | Quelltext bearbeiten]- Der vollständige Graph ist der einzige kubische Graph mit 4 Knoten.
- Ein kubischen Graph mit 6 Knoten.
- Der Petersen-Graph als Beispiel für einen kubischen Graphen.
Weblinks
[Bearbeiten | Quelltext bearbeiten]Commons: 3-regular graphs – Sammlung von Bildern, Videos und Audiodateien
- Weisstein, Eric W.: Cubic Graph. In: MathWorld (englisch).


 French
French Deutsch
Deutsch