Modi mit begrenzten Transpositionsmöglichkeiten – Wikipedia
Die sieben Modi mit begrenzten Transpositionsmöglichkeiten des Komponisten Olivier Messiaen systematisieren die bereits seit Franz Liszt, Claude Debussy, Maurice Ravel, Alexander Skrjabin und Béla Bartók bekannten distanziellen Oktavteilungen (gleichstufige bzw. periodisch-alternierende Intervallketten) und verwenden diese auch schon als „flächendeckendes“ Skalenmaterial für lange distanzharmonische Verläufe. Messiaen betrachtet die chromatische Tonleiter (einer in 12 gleiche Tonschritte unterteilten Oktave 12-EDO) als „unser derzeitiges chromatisches System“ (S. 56) und daher als Obermenge und nicht als eigenen Modus. Bereits im Vorwort zu seinem Orgelzyklus La Nativité du Seigneur (1935) und in seinem Buch Technique de mon langage musical (1944) erläuterte Messiaen diese Modi.[1]
Die Modi
[Bearbeiten | Quelltext bearbeiten]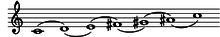
1. Modus
[Bearbeiten | Quelltext bearbeiten]Der gleichstufige erste Modus ist die Ganztonleiter und teilt damit die Oktave in sechs gleiche Intervalle. Sie ist deswegen nur noch einmal transponierbar, weil jede weitere Transposition mit einer der bereits zuvor verwendeten Gestalten zusammenfallen würde. In Olivier Messiaens Sprachregelung gilt die von C aus beginnende Gestalt („Grundgestalt“) bereits als die 1. Transposition. Als Zahlengestalt sieht dieser Modus so aus: 222222 und besitzt daher keine Umkehrung analog zu Akkorden. (2=Ganztonschritt)

2. Modus
[Bearbeiten | Quelltext bearbeiten]Der zweite Modus beruht auf der Kleinterzteilung der Oktave und entspricht der seit dem 19. Jahrhundert bekannten bzw. seither bereits vielfach verwendeten alternierenden Achtstufigkeit (auch Oktatonie genannt), also einer Skala von acht Tönen, die jeweils im periodischen Wechsel aus Halb- und Ganztonschritten besteht. Dieser Modus unterteilt die kleine Terz als Keimzelle in einen Halbtonschritt und einen Ganztonschritt, er ist dreifach transponierbar, denn ab einer vierten Transposition würden sich nur noch Wiederholungen der zuvor bereits verwendeten Skalen ergeben. In Olivier Messiaens Sprachregelung gilt die von C aus mit dem Halbtonschritt beginnende Gestalt („Grundgestalt“) bereits als die 1. Transposition. Als Zahlengestalt sieht dieser Modus so aus: 12121212 und besitzt eine Umkehrung (21212121). (1 = Halbtonschritt, 2 = Ganztonschritt)
In der Jazzharmonielehre ist diese Tonleiter auch als HTGT-Tonleiter (Halbton-Ganzton) bekannt und wird dort vorwiegend über Dominanten (z. B. Dominantseptakkord mit kleiner None, mit übermäßiger None, mit übermäßiger Undezime und großer Tredezime) eingesetzt. Eine weitere Bezeichnung lautet Verminderte Skala.

3. Modus
[Bearbeiten | Quelltext bearbeiten]Der dritte Modus beruht dann auf der Großterzteilung der Oktave und unterteilt die große Terz als Keimzelle des Modus in einen Ganzton und zwei Halbtöne; er ist viermal transponierbar. In der hierbei verwendeten Sprachregelung Olivier Messiaens gilt die von C aus mit dem Ganztonschritt beginnende Gestalt bereits als die 1. Transposition. Als Zahlengestalt sieht dieser Modus so aus: 211211211 und besitzt zwei Umkehrungen (112112112 und 121121121)




4.–7. Modus
[Bearbeiten | Quelltext bearbeiten]Die Modi 4. bis 7. beruhen auf der Halboktave (Tritonus) und sind damit sechsmal transponierbar. Als Zahlengestalt sehen sie übersichtlich so aus (3 = kleine Terz, 4 = große Terz):
4. Modus: 11311131 mit drei Umkehrungen (13111311, 31113111 und 11131113)
5. Modus: 141141 mit zwei Umkehrungen (411411 und 114114)
6. Modus: 22112211 mit drei Umkehrungen (21122112, 11221122 und 12211221)
7. Modus: 1112111121 mit vier Umkehrungen (1121111211, 1211112111, 2111121111 und 1111211112)
Verwendung und Charakteristik
[Bearbeiten | Quelltext bearbeiten]Die Modi dienen – genauso wie dies auch bei den verschiedenen Tonarten oder Kirchentonarten in der überlieferten diatonischen Tonalität vergangener Jahrhunderte der Fall ist – nicht nur als Grundlage des melodischen Materials, sondern selbstverständlich auch als Grundlage der begleitenden Akkorde. Die Begleitakkorde im 2. Modus sind beispielsweise meistens entweder Dur- und Molldreiklänge auf jener Grundton-Trägerachse, die aus der aktuellen Transposition der diesem Modus zugrundeliegenden Kleinterzteilung der Oktave hervorgeht (z. B. in der sogenannten 1. Transposition des 2. Modus ist die Grundton-Trägerachse c-es-fis-a) oder aber auch viertönige Akkorde, die etwa aus einem Dur-Quartsextakkord mit hinzugefügtem Tritonus bzw. #11 oder mit hinzugefügter großer Sexte bzw. Tredezime oder aber aus der Verknüpfung eines quintlosen Dominantseptimakkordes mit hinzugefügter großer Sexte bzw. Tredezime bestehen.
Messiaen spricht von „begrenzt transponierbaren“ Modi, weil die traditionellen diatonischen Skalen (z. B. die kirchentonalen Modi oder auch Dur und Moll) bekanntlich elfmal transponierbar sind, bevor die Ausgangsposition (Originalgestalt) wieder erreicht wird. Anmerkung: Auch die überlieferten diatonischen Skalen sind nicht unbegrenzt transponierbar. An deren insgesamt zwölf Erscheinungsformen gemessen, kann natürlich die nur zweifache, dreifache, vierfache oder sechsfache Transponierbarkeit als „begrenzt“ gelten.
Ein achter Modus
[Bearbeiten | Quelltext bearbeiten]Der amerikanische Musikwissenschaftler John Schuster-Craig hat 1990 in der Nr. 51 der Fachzeitschrift The Music Review (BlackBearPress Ltd. (Hrsg.): Geoffrey Sharp) einen Beitrag veröffentlicht, in welchem er nachweist, dass es tatsächlich einen weiteren, achten Modus gibt, der nicht 12-mal transponierbar ist, den Messiaen jedoch nicht entdeckt oder vergessen habe. Er hat folgenden Aufbau (vgl. oben): 131313 bzw. 313131 und wäre viermal transponierbar (C = 1. Transposition analog zu Messiaens Sprachgebrauch). Dieser wird also aus abwechselnd einer kleinen Sekunde und einer kleinen Terz gebildet und prominente Komponisten des 19. Jh. haben ihn intuitiv benutzt: Franz Liszt in seiner Faust-Sinfonie, Rimski-Korsakow in seiner Sinfonischen Dichtung Sadko und seiner Oper Der goldene Hahn und schließlich sogar Béla Bartók sehr exponiert im dritten Satz seines Konzerts für Orchester (Takte 10–11 + Takte 23–27).
Mathematische Analyse der Modi
[Bearbeiten | Quelltext bearbeiten]Messiaen postulierte für seine Modi eine mathematische Vollständigkeit. Dem widerspricht die Entdeckung des achten Modus durch John Schuster-Craigh. Mathematisch lassen sich die Modi mit begrenzten Transpositionsmöglichkeiten als translationsinvariante Skalengebilde im Ambitus einer Oktave bezeichnen und auf diese Weise systematisieren. Die mögliche Anzahl aller Modi in diesem Ambitus lässt sich durch Abzählung der geordneten Partitionen der Zahlen 6 und 4 ermitteln. Anders ausgedrückt: Gesucht sind alle Möglichkeiten, die es gibt, um mit natürlichen Zahlen die Summe 12 zu erreichen. (1+1+1+1+1+1+1+1+1+1+1+1 = 12 = 6+6 sind dabei die Extrembeispiele) Durch diesen Vorgang entstehen theoretisch 38 Modi. Bei 22 von ihnen handelt es sich aber lediglich um bloße Umkehrungen voneinander, die keine weitere Varianz darstellen. Streicht man diese, so erhält man 16 Skalen, welche die von Messiaen vorgegebenen Bedingungen erfüllen. Von diesen zählte Messiaen sieben zu seinen Modi, von sieben weiteren begründet er, weshalb er sie nicht zu seinen Modi zählt. Zwei weitere ließ er allerdings unerwähnt; einer dieser zwei ist der oben erwähnte achte Modus, der neunte Modus hat folgenden Aufbau: 2424 bzw. 4242 und wäre analog zu den Modi 4–7 sechsmal transponierbar.
| Tabelle der möglichen Skalen | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

unvollständig bedeutet, dass Messiaen die Skalen 1 2 3 1 2 3 sowie 1 3 2 1 3 2 als „unvollständige Modi 2“ (S. 59) bezeichnet (1 2 3 1 2 3 = 1 2 1+2 1 2 1+2) und ihnen damit keinen eigenen Modus zugesteht (nebenbei bemerkt: diese sind die einzigen Skalen, welche nicht achsensymmetrisch sind). Dieses Argument ist allerdings wenig stichhaltig, da er der Skala 1 1 4 1 1 4 (= 1 1 1+3 1 1 1+3 = 4. Modus) den Status als 5. Modus zuweist. Demzufolge wäre der 1. Modus ebenfalls ein unvollständiger 3., 6. oder 7. Modus usw. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Literatur
[Bearbeiten | Quelltext bearbeiten]- Gárdonyi-Nordhoff: Harmonik. Wolfenbüttel: Möseler Verlag 2002, Kapitel 15 und 16
- Koepf, Siegfried: Zu Messiaens „Modi mit begrenzter Transpositionsmöglichkeit“. In: Organ – Journal für die Orgel, Heft 4/2008
- Messiaen, Olivier: Technique de mon langage musical: Leduc, Paris 1944
Weblinks
[Bearbeiten | Quelltext bearbeiten]Einzelnachweise
[Bearbeiten | Quelltext bearbeiten]- ↑ Deutsch: Technik meiner musikalischen Sprache. Paris 1966.


 French
French Deutsch
Deutsch