Pythagoreische Addition – Wikipedia

Als pythagoreische Addition wird eine der üblichen Addition ähnliche Rechenoperation bezeichnet, bei der die Summe der Quadrate mehrerer Größen berechnet und daraus die Quadratwurzel gebildet wird.^[1]

Ausgedrückt als Formel ergibt sich die pythagoreische oder geometrische Summe ${\displaystyle S}$ aus den Größen ${\displaystyle a,\;b,\;c,\;\dotsc }$ durch:

${\displaystyle S={\sqrt {a^{2}+b^{2}+c^{2}+\,\dotsb \ }}\ .}$

Ihren Namen trägt die Operation in Anlehnung an den Satz des Pythagoras: ${\displaystyle a^{2}+b^{2}=c^{2}}$, wenn ${\displaystyle a}$ und ${\displaystyle b}$ die Kathetenlängen und ${\displaystyle c}$ die Hypotenusenlänge eines rechtwinkligen Dreiecks darstellen.

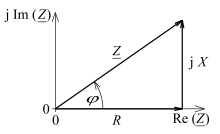
Verwendung findet die pythagoreische Addition in vielen Gebieten der Wissenschaft und Technik, wie beispielsweise der Berechnung des Effektivwerts einer Stromstärke, eines Wechselstromwiderstands oder einer Messunsicherheit gemäß dem Gaußschen Fehlerfortpflanzungsgesetz. Dabei lassen sich zwei Besonderheiten der Rechnung zu Nutze machen. Zum einen sind die miteinander addierten Terme durch die Quadrierung stets positiv, wodurch das Ergebnis unabhängig vom Vorzeichen der beitragenden Werte wird. Zum anderen ist das Ergebnis stets kleiner als die gewöhnliche Summe der Beträge (oder das Ergebnis ist identisch bei nur einem Wert). Im Falle der Fehlerrechnung wird dadurch der möglichen gegenseitigen Kompensation einzelner zufälliger Abweichungen Rechnung getragen. Somit eignet sich die pythagoreische Addition zur Abschätzung der Unsicherheit eines Ergebnisses bei voneinander unabhängig streuenden Einzelwerten.

Weiterhin findet sie oft als arithmetisches Hilfsmittel Verwendung, wie beispielsweise zum Vereinfachen sinus- und kosinusabhängiger Terme mit dem „trigonometrischen Pythagoras“.

• Euklidische Norm

1. ↑ Bertram Huppert: Angewandte lineare Algebra. Walter de Gruyter, Berlin, 1990, ISBN 3-11-012107-7, S. 635.
   Walter Geiger, Willi Kotte: Handbuch Qualität: Grundlagen und Elemente des Qualitätsmanagements; Systeme – Perspektiven. Vieweg + Teubner, Wiesbaden, 2005, ISBN 3-528-33357-X.