Tetragonales Kristallsystem – Wikipedia

Roter Zirkon (Größe: 1,0 cm) aus Gilgit, Pakistan

Phosgenit, ausgestellt im Royal Ontario Museum

Das Tetragonale Kristallsystem gehört zu den sieben Kristallsystemen in der Kristallographie. Es umfasst alle Punktgruppen, die in genau einer Richtung eine vierzählige Dreh- oder Drehinversionsachse besitzen.

Punktgruppen

Das tetragonale Kristallsystem umfasst die Punktgruppen $\ 4,\,{\bar {4}},\,4/m,\,422,\,4mm,\,{\bar {4}}2m$ und $\ 4/mmm$ . Sie bilden die tetragonale Kristallfamilie und können mit dem tetragonalen Gittersystem beschrieben werden.

Gittersystem

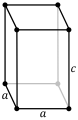
Das tetragonale Gittersystem hat die Holoedrie $\ 4/mmm$ . Analog zu den anderen wirteligen Kristallsystemen wird die vierzählige Achse in die Richtung der c-Gitterachse gelegt. Wie im monoklinen liegen die beiden anderen Richtungen senkrecht zur c-Achse und müssen – aufgrund der Vierzähligkeit der c-Achse – darüber hinaus auch gleiche Länge besitzen und senkrecht zueinander stehen. Daher gibt es in diesem Kristallsystem nur die beiden Gitterkonstanten a und c und es ergeben sich folgende Bedingungen:

$a\ =b\ \neq \ c\$
$\alpha \ =\beta \ =\gamma \ =90^{\circ }$

Bravaisgitter

Tetragonal primitives Gitter: tP
Tetragonal innenzentriertes Gitter: tI

Im tetragonalen Kristallsystem gibt es zwei Bravaisgitter, das primitive und das innenzentrierte. Das flächenzentrierte Bravaisgitter entspricht nicht der Standardaufstellung, da diese Gitter immer durch ein innenzentriertes Gitter mit halb so großer Elementarzelle beschrieben werden kann. Man erhält das innenzentrierte Gitter aus dem flächenzentrierten, indem man die a-Achsen um 45° um die c-Achse dreht und um den Faktor ${\frac {1}{\sqrt {2}}}$ verkleinert.

Punktgruppen im tetragonalen Kristallsystem und ihre physikalischen Eigenschaften

Zur Beschreibung der tetragonalen Kristallklassen in Hermann-Mauguin-Symbolik werden die Symmetrieoperationen bezüglich vorgegebener Richtungen (Blickrichtungen) im Gittersystem angegeben. Die Blickrichtung des ersten Symbols ist die c-Achse (<001>), des zweiten Symbols die a-Achse (<100>) und des dritten Symbols die Flächendiagonale der c-Fläche (<110>).

Charakteristisch für die tetragonalen Raumgruppen ist eine 4 (4) an erster Stelle, aber keine 3 (3) an der zweiten Stelle des Raumgruppensymbols.

Punktgruppe (Kristallklasse)								Physikalische Eigenschaften^{[Anm. 1]}				Beispiele
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Internationales Symbol (Hermann-Mauguin)		Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
Nr.	Kristallsystem	Name	Schoenflies-Symbol	Voll	Kurz	Laueklasse	Zugehörige Raumgruppen (Nr.)	Enantiomorphie	Optische Aktivität	Pyroelektrizität	Piezoelektrizität; SHG-Effekt
9	tetragonal	tetragonal-pyramidal	C₄	4	4	4/m	75–80	+	+	+ [001]	+	Pinnoit Percleveit‑(Ce)
10		tetragonal-disphenoidisch	S₄	4	4		81–82	–	+	–	+	Schreibersit Cahnit
11		tetragonal-dipyramidal	C_4h	4/m	4/m		83–88	–	–	–	–	Scheelit Baotit
12		tetragonal-trapezoedrisch	D₄	422	422	4/mmm	89–98	+	+	–	+	Cristobalit Maucherit
13		ditetragonal-pyramidal	C_4v	4mm	4mm		99–110	–	–	+ [001]	+	Lenait Diaboleit
14		tetragonal-skalenoedrisch	D_2d (V_d)	42m bzw. 4m2	42m		111–122	–	+	–	+	Chalkopyrit Stannit
15		ditetragonal-dipyramidal	D_4h	4/m2/m2/m	4/mmm		123–142	–	–	–	–	Rutil Zirkon
↑ Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist. Für die Pyroelektrizität ist, sofern vorhanden, auch die Richtung des pyroelektrischen Vektors angegeben.

Weitere tetragonal kristallisierende chemische Stoffe siehe Kategorie:Tetragonales Kristallsystem

Literatur

Hahn, Theo (Hrsg.): International Tables for Crystallography Vol. A D. Reidel publishing Company, Dordrecht 1983, ISBN 90-277-1445-2
D. Schwarzenbach: Kristallographie. Springer Verlag, Berlin 2001, ISBN 3-540-67114-5
Will Kleber, Hans-Joachim Bautsch, Joachim Bohm, Detlef Klimm: Einführung in die Kristallographie. 19. Auflage. Oldenbourg Wissenschaftsverlag, 2010, ISBN 978-3-486-59075-3.
Walter Borchard-Ott: Kristallographie. 7. Auflage. Springer Verlag, Berlin 2009, ISBN 978-3-540-78270-4

[Hinweise-1] Bei den Angaben zu den physikalischen Eigenschaften bedeutet „−“ aufgrund der Symmetrie verboten und „+“ erlaubt. Über die Größenordnung der optischen Aktivität, Pyro- und Piezoelektrizität sowie des SHG-Effekts kann rein aufgrund der Symmetrie keine Aussage getroffen werden. Man kann aber davon ausgehen, dass stets eine zumindest schwache Ausprägung der Eigenschaft vorhanden ist. Für die Pyroelektrizität ist, sofern vorhanden, auch die Richtung des pyroelektrischen Vektors angegeben.

[Anm. 1]