Zehnerpotenz – Wikipedia

Zehnerpotenzen, auch Stufenzahlen genannt, sind Potenzen mit der Basis 10 und einem ganzzahligen Exponenten. Eine wichtige Anwendung der Zehnerpotenzen ist die Schreibweise von Gleitkommazahlen, beispielsweise in der technischen Notation.

Zu Zahlennamen von Zehnerpotenzen siehe auch im entsprechenden Abschnitt im Artikel Zahlennamen. Hier die wichtigsten Zahlennamen von Zehnerpotenzen einschließlich zugehöriger SI-Vorsätze:

Name	Zahl in Exponential- schreibweise	Zahl in Dezimalschreibweise	Vorsatz[1]
			Name	Zei- chen
Quintillionstel	${\displaystyle 10^{-30}}$	${\displaystyle 0{,}000\,000\,000\,000\,000\,000\,000\,000\,000\,001}$	Quekto	q
Quadrilliardstel	${\displaystyle 10^{-27}}$	${\displaystyle 0{,}000\,000\,000\,000\,000\,000\,000\,000\,001}$	Ronto	r
Quadrillionstel	${\displaystyle 10^{-24}}$	${\displaystyle 0{,}000\,000\,000\,000\,000\,000\,000\,001}$	Yokto	y
Trilliardstel	${\displaystyle 10^{-21}}$	${\displaystyle 0{,}000\,000\,000\,000\,000\,000\,001}$	Zepto	z
Trillionstel	${\displaystyle 10^{-18}}$	${\displaystyle 0{,}000\,000\,000\,000\,000\,001}$	Atto	a
Billiardstel	${\displaystyle 10^{-15}}$	${\displaystyle 0{,}000\,000\,000\,000\,001}$	Femto	f
Billionstel	${\displaystyle 10^{-12}}$	${\displaystyle 0{,}000\,000\,000\,001}$	Piko	p
Milliardstel	${\displaystyle 10^{-9}}$	${\displaystyle 0{,}000\,000\,001}$	Nano	n
Millionstel	${\displaystyle 10^{-6}}$	${\displaystyle 0{,}000\,001}$	Mikro	μ
Hunderttausendstel	${\displaystyle 10^{-5}}$	${\displaystyle 0{,}000\,01}$
Zehntausendstel	${\displaystyle 10^{-4}}$	${\displaystyle 0{,}000\,1}$
Tausendstel	${\displaystyle 10^{-3}}$	${\displaystyle 0{,}001}$	Milli	m
Hundertstel	${\displaystyle 10^{-2}}$	${\displaystyle 0{,}01}$	Zenti	c
Zehntel	${\displaystyle 10^{-1}}$	${\displaystyle 0{,}1}$	Dezi	d
Eins	${\displaystyle 10^{0}}$	${\displaystyle 1}$
Zehn	${\displaystyle 10^{1}}$	${\displaystyle 10}$	Deka	da
Hundert	${\displaystyle 10^{2}}$	${\displaystyle 100}$	Hekto	h
Tausend	${\displaystyle 10^{3}}$	${\displaystyle 1\,000}$	Kilo	k
Zehntausend	${\displaystyle 10^{4}}$	${\displaystyle 10\,000}$
Hunderttausend	${\displaystyle 10^{5}}$	${\displaystyle 100\,000}$
Million	${\displaystyle 10^{6}}$	${\displaystyle 1\,000\,000}$	Mega	M
Milliarde	${\displaystyle 10^{9}}$	${\displaystyle 1\,000\,000\,000}$	Giga	G
Billion	${\displaystyle 10^{12}}$	${\displaystyle 1\,000\,000\,000\,000}$	Tera	T
Billiarde	${\displaystyle 10^{15}}$	${\displaystyle 1\,000\,000\,000\,000\,000}$	Peta	P
Trillion	${\displaystyle 10^{18}}$	${\displaystyle 1\,000\,000\,000\,000\,000\,000}$	Exa	E
Trilliarde	${\displaystyle 10^{21}}$	${\displaystyle 1\,000\,000\,000\,000\,000\,000\,000}$	Zetta	Z
Quadrillion	${\displaystyle 10^{24}}$	${\displaystyle 1\,000\,000\,000\,000\,000\,000\,000\,000}$	Yotta	Y
Quadrilliarde	${\displaystyle 10^{27}}$	${\displaystyle 1\,000\,000\,000\,000\,000\,000\,000\,000\,000}$	Ronna	R
Quintillion	${\displaystyle 10^{30}}$	${\displaystyle 1\,000\,000\,000\,000\,000\,000\,000\,000\,000\,000}$	Quetta	Q

Der Exponent gibt dabei die Zahl der Nullen zur Dezimalschreibweise der Zehnerpotenz an. Wenn dort 10⁶ (zehn hoch sechs) steht, dann bedeutet das eine Eins mit 6 Nullen (Million).

Für Maßeinheiten definiert das Internationale Einheitensystem (SI) zweisilbige Vorsätze, die die Bedeutung von Zehnerpotenzfaktoren haben, wie sie in vorstehender Tabelle enthalten sind. Bei messbaren Größen kann das Schreiben von langen Ziffernfolgen oder von Zehnerpotenzen vielfach vermieden werden. Beispiele:

17 000 Meter = 1,7·10⁴ Meter = 17 Kilometer = 17 km

1 Kilowattstunde = 3 600 000 Joule = 3.6e⁶ J = 3,6 MJ

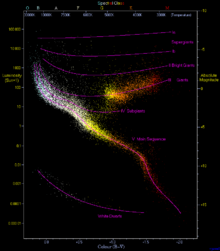
Da unser übliches Zahlensystem, das Dezimalsystem (zu lat. decimus „der Zehnte“), auf Zehnerpotenzen beruht, können mit diesen auch sehr große und sehr kleine Zahlen kompakt geschrieben werden. Diese Schreibweise bildet die Grundlage der wissenschaftlichen Notation (kurz SCI für englisch scientific), in der eine Dezimalzahl auf eine normierte Mantisse und einen Potenzfaktor zur Basis 10 umgeschrieben wird.

Dazu als Beispiele:

4.711e³ = 4711

4.711e² = 471,1

4.711e^-9 = 0,000 000 004 711

Auch die Achsen von Diagrammen werden oft nicht linear, sondern in Zehnerpotenzen als logarithmische Skala geteilt, wenn es um sehr große Wertebereiche geht. Ein Beispiel aus der Astronomie – die man ja mit „astronomisch großen Zahlen“ assoziiert – ist das Hertzsprung-Russell-Diagramm, das im nebenstehenden Bild auf der Ordinate eine Skala von 0,000 01 bis 100 000 Einheiten der Sonnen-Leuchtkraft L₀ zeigt. Dann liegt aber z. B. in der Mitte zwischen 10 und 100 L₀ nicht der Wert 20 oder 50, sondern rund 32 L₀. Dieser Wert ist nicht das arithmetische, sondern das geometrische Mittel von 10¹ und 10², das ist 10^1,5 bzw. die Wurzel aus 10·100.

Es gibt einige einfache Rechenregeln für das Rechnen mit Zehnerpotenzen:

• Multipliziert man eine natürliche Zahl mit einer Stufenzahl, so werden die Nullen der Stufenzahl an die natürliche Zahl angehängt.
• Multipliziert man einen Dezimalbruch mit einer Stufenzahl, so rückt das Komma um so viele Stellen nach rechts, wie die Stufenzahl Nullen hat.
• Dividiert man einen Dezimalbruch durch eine Stufenzahl, so rückt das Komma um so viele Stellen nach links, wie die Stufenzahl Nullen hat.

Wiktionary: Zehnerpotenz – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

1. ↑ [1]. Die „SI-Broschüre“, 9. Ausgabe, 2019, aktualisiert 2022. S. 31 und 143. Abgerufen am 29. November 2023