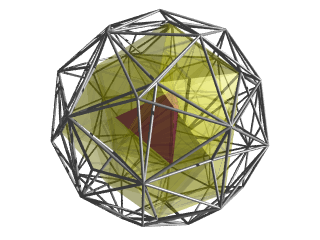
600-cell
This article may require cleanup to meet Wikipedia's quality standards. The specific problem is: Excessive explanatory footnotes, some of which include other explanatory footnotes, which include other explanatory footnotes, and so on. Linearize by trimming for brevity, inserting into main text, or spawning subarticle(s). (March 2024) |
| 600-cell | |
|---|---|
 Schlegel diagram, vertex-centered (vertices and edges) | |
| Type | Convex regular 4-polytope |
| Schläfli symbol | {3,3,5} |
| Coxeter diagram | |
| Cells | 600 ({3,3}) |
| Faces | 1200 {3} |
| Edges | 720 |
| Vertices | 120 |
| Vertex figure |  icosahedron |
| Petrie polygon | 30-gon |
| Coxeter group | H4, [3,3,5], order 14400 |
| Dual | 120-cell |
| Properties | convex, isogonal, isotoxal, isohedral |
| Uniform index | 35 |

In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also known as the C600, hexacosichoron[1] and hexacosihedroid.[2] It is also called a tetraplex (abbreviated from "tetrahedral complex") and a polytetrahedron, being bounded by tetrahedral cells.
The 600-cell's boundary is composed of 600 tetrahedral cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. It is the 4-dimensional analogue of the icosahedron, since it has five tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex. Its dual polytope is the 120-cell.
Geometry
[edit]The 600-cell is the fifth in the sequence of 6 convex regular 4-polytopes (in order of complexity and size at the same radius).[a] It can be deconstructed into twenty-five overlapping instances of its immediate predecessor the 24-cell,[5] as the 24-cell can be deconstructed into three overlapping instances of its predecessor the tesseract (8-cell), and the 8-cell can be deconstructed into two instances of its predecessor the 16-cell.[6]
The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length. The 24-cell's edge length equals its radius, but the 600-cell's edge length is ~0.618 times its radius,[7] which is the golden ratio.
| Regular convex 4-polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Symmetry group | A4 | B4 | F4 | H4 | |||
| Name | 5-cell Hyper-tetrahedron | 16-cell Hyper-octahedron | 8-cell Hyper-cube | 24-cell
| 600-cell Hyper-icosahedron | 120-cell Hyper-dodecahedron | |
| Schläfli symbol | {3, 3, 3} | {3, 3, 4} | {4, 3, 3} | {3, 4, 3} | {3, 3, 5} | {5, 3, 3} | |
| Coxeter mirrors | |||||||
| Mirror dihedrals | 𝝅/3 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/4 𝝅/2 𝝅/2 𝝅/2 | 𝝅/4 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/4 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | 𝝅/3 𝝅/3 𝝅/5 𝝅/2 𝝅/2 𝝅/2 | 𝝅/5 𝝅/3 𝝅/3 𝝅/2 𝝅/2 𝝅/2 | |
| Graph | 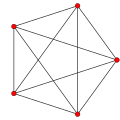 | 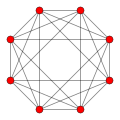 |  | 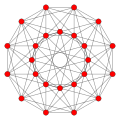 |  |  | |
| Vertices | 5 tetrahedral | 8 octahedral | 16 tetrahedral | 24 cubical | 120 icosahedral | 600 tetrahedral | |
| Edges | 10 triangular | 24 square | 32 triangular | 96 triangular | 720 pentagonal | 1200 triangular | |
| Faces | 10 triangles | 32 triangles | 24 squares | 96 triangles | 1200 triangles | 720 pentagons | |
| Cells | 5 tetrahedra | 16 tetrahedra | 8 cubes | 24 octahedra | 600 tetrahedra | 120 dodecahedra | |
| Tori | 1 5-tetrahedron | 2 8-tetrahedron | 2 4-cube | 4 6-octahedron | 20 30-tetrahedron | 12 10-dodecahedron | |
| Inscribed | 120 in 120-cell | 675 in 120-cell | 2 16-cells | 3 8-cells | 25 24-cells | 10 600-cells | |
| Great polygons | 2 squares x 3 | 4 rectangles x 4 | 4 hexagons x 4 | 12 decagons x 6 | 100 irregular hexagons x 4 | ||
| Petrie polygons | 1 pentagon x 2 | 1 octagon x 3 | 2 octagons x 4 | 2 dodecagons x 4 | 4 30-gons x 6 | 20 30-gons x 4 | |
| Long radius | |||||||
| Edge length | |||||||
| Short radius | |||||||
| Area | |||||||
| Volume | |||||||
| 4-Content | |||||||
Coordinates
[edit]Unit radius Cartesian coordinates
[edit]The vertices of a 600-cell of unit radius centered at the origin of 4-space, with edges of length 1/φ ≈ 0.618 (where φ = 1 + √5/2 ≈ 1.618 is the golden ratio), can be given[8] as follows:
8 vertices obtained from
- (0, 0, 0, ±1)
by permuting coordinates, and 16 vertices of the form:
- (±1/2, ±1/2, ±1/2, ±1/2)
The remaining 96 vertices are obtained by taking even permutations of
- (±φ/2, ±1/2, ±φ−1/2, 0)
Note that the first 8 are the vertices of a 16-cell, the second 16 are the vertices of a tesseract, and those 24 vertices together are the vertices of a 24-cell. The remaining 96 vertices are the vertices of a snub 24-cell, which can be found by partitioning each of the 96 edges of another 24-cell (dual to the first) in the golden ratio in a consistent manner.[9]
When interpreted as quaternions,[b] these are the unit icosians.
In the 24-cell, there are squares, hexagons and triangles that lie on great circles (in central planes through four or six vertices).[c] In the 600-cell there are twenty-five overlapping inscribed 24-cells, with each vertex and square shared by five 24-cells, and each hexagon or triangle shared by two 24-cells.[e] In each 24-cell there are three disjoint 16-cells, so in the 600-cell there are 75 overlapping inscribed 16-cells.[f] Each 16-cell constitutes a distinct orthonormal basis for the choice of a coordinate reference frame.
The 60 axes and 75 16-cells of the 600-cell constitute a geometric configuration, which in the language of configurations is written as 605754 to indicate that each axis belongs to 5 16-cells, and each 16-cell contains 4 axes.[10] Each axis is orthogonal to exactly 15 others, and these are just its companions in the 5 16-cells in which it occurs.
Hopf spherical coordinates
[edit]In the 600-cell there are also great circle pentagons and decagons (in central planes through ten vertices).[11]
Only the decagon edges are visible elements of the 600-cell (because they are the edges of the 600-cell). The edges of the other great circle polygons are interior chords of the 600-cell, which are not shown in any of the 600-cell renderings in this article (except where shown as dashed lines).[k]
By symmetry, an equal number of polygons of each kind pass through each vertex; so it is possible to account for all 120 vertices as the intersection of a set of central polygons of only one kind: decagons, hexagons, pentagons, squares, or triangles. For example, the 120 vertices can be seen as the vertices of 15 pairs of completely orthogonal squares which do not share any vertices, or as 100 dual pairs of non-orthogonal hexagons between which all axis pairs are orthogonal, or as 144 non-orthogonal pentagons six of which intersect at each vertex. This latter pentagonal symmetry of the 600-cell is captured by the set of Hopf coordinates[13] (𝜉i, 𝜂, 𝜉j)[n] given as:
- ({<10}𝜋/5, {≤5}𝜋/10, {<10}𝜋/5)
where {<10} is the permutation of the ten digits (0 1 2 3 4 5 6 7 8 9) and {≤5} is the permutation of the six digits (0 1 2 3 4 5). The 𝜉i and 𝜉j coordinates range over the 10 vertices of great circle decagons; even and odd digits label the vertices of the two great circle pentagons inscribed in each decagon.[o]
Structure
[edit]Polyhedral sections
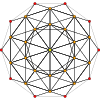
[edit]The mutual distances of the vertices, measured in degrees of arc on the circumscribed hypersphere, only have the values 36° = 𝜋/5, 60° = 𝜋/3, 72° = 2𝜋/5, 90° = 𝜋/2, 108° = 3𝜋/5, 120° = 2𝜋/3, 144° = 4𝜋/5, and 180° = 𝜋. Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron,[p] at 60° and 120° the 20 vertices of a dodecahedron, at 72° and 108° the 12 vertices of a larger icosahedron, at 90° the 30 vertices of an icosidodecahedron, and finally at 180° the antipodal vertex of V.[14][15][16] These can be seen in the H3 Coxeter plane projections with overlapping vertices colored.[17]
These polyhedral sections are solids in the sense that they are 3-dimensional, but of course all of their vertices lie on the surface of the 600-cell (they are hollow, not solid). Each polyhedron lies in Euclidean 4-dimensional space as a parallel cross section through the 600-cell (a hyperplane). In the curved 3-dimensional space of the 600-cell's boundary surface envelope, the polyhedron surrounds the vertex V the way it surrounds its own center. But its own center is in the interior of the 600-cell, not on its surface. V is not actually at the center of the polyhedron, because it is displaced outward from that hyperplane in the fourth dimension, to the surface of the 600-cell. Thus V is the apex of a 4-pyramid based on the polyhedron.
Golden chords
[edit]
The 120 vertices are distributed[18] at eight different chord lengths from each other. These edges and chords of the 600-cell are simply the edges and chords of its five great circle polygons.[19] In ascending order of length, they are √0.𝚫, √1, √1.𝚫, √2, √2.𝚽, √3, √3.𝚽, and √4.[s]
Notice that the four hypercubic chords of the 24-cell (√1, √2, √3, √4)[c] alternate with the four new chords of the 600-cell's additional great circles, the decagons and pentagons. The new golden chord lengths are necessarily square roots of fractions, but very special fractions related to the golden ratio[q] including the two golden sections of √5, as shown in the diagram.[r]
Boundary envelopes
[edit]
The 600-cell rounds out the 24-cell by adding 96 more vertices between the 24-cell's existing 24 vertices,[u] in effect adding twenty-four more overlapping 24-cells inscribed in the 600-cell.[f] The new surface thus formed is a tessellation of smaller, more numerous cells[v] and faces: tetrahedra of edge length 1/φ ≈ 0.618 instead of octahedra of edge length 1. It encloses the √1 edges of the 24-cells, which become invisible interior chords in the 600-cell, like the √2 and √3 chords.

Since the tetrahedra are made of shorter triangle edges than the octahedra (by a factor of 1/φ, the inverse golden ratio), the 600-cell does not have unit edge-length in a unit-radius coordinate system the way the 24-cell and the tesseract do; unlike those two, the 600-cell is not radially equilateral. Like them it is radially triangular in a special way,[z] but one in which golden triangles rather than equilateral triangles meet at the center.[aa] Only a few uniform polytopes have this property, including the four-dimensional 600-cell, the three-dimensional icosidodecahedron, and the two-dimensional decagon. (The icosidodecahedron is the equatorial cross section of the 600-cell, and the decagon is the equatorial cross section of the icosidodecahedron.) Radially golden polytopes are those which can be constructed, with their radii, from golden triangles.
The boundary envelope of 600 small tetrahedral cells wraps around the twenty-five envelopes of 24 octahedral cells (adding some 4-dimensional space in places between these curved 3-dimensional envelopes). The shape of those interstices must be an octahedral 4-pyramid of some kind, but in the 600-cell it is not regular.[ab]
Geodesics
[edit]The vertex chords of the 600-cell are arranged in geodesic great circle polygons of five kinds: decagons, hexagons, pentagons, squares, and triangles.[22]

The √0.𝚫 = 𝚽 edges form 72 flat regular central decagons, 6 of which cross at each vertex.[p] Just as the icosidodecahedron can be partitioned into 6 central decagons (60 edges = 6 × 10), the 600-cell can be partitioned into 72 decagons (720 edges = 72 × 10). The 720 √0.𝚫 edges divide the surface into 1200 triangular faces and 600 tetrahedral cells: a 600-cell. The 720 edges occur in 360 parallel pairs, √3.𝚽 apart. As in the decagon and the icosidodecahedron, the edges occur in golden triangles which meet at the center of the polytope. The 72 great decagons can be divided into 6 sets of 12 non-intersecting Clifford parallel geodesics,[af] such that only one decagonal great circle in each set passes through each vertex, and the 12 decagons in each set reach all 120 vertices.[24]
The √1 chords form 200 central hexagons (25 sets of 16, with each hexagon in two sets),[d] 10 of which cross at each vertex[ag] (4 from each of five 24-cells that meet at the vertex, with each hexagon in two of those 24-cells).[i] Each set of 16 hexagons consists of the 96 edges and 24 vertices of one of the 25 overlapping inscribed 24-cells. The √1 chords join vertices which are two √0.𝚫 edges apart. Each √1 chord is the long diameter of a face-bonded pair of tetrahedral cells (a triangular bipyramid), and passes through the center of the shared face. As there are 1200 faces, there are 1200 √1 chords, in 600 parallel pairs, √3 apart. The hexagonal planes are non-orthogonal (60 degrees apart) but they occur as 100 dual pairs in which all 3 axes of one hexagon are orthogonal to all 3 axes of its dual.[25] The 200 great hexagons can be divided into 10 sets of 20 non-intersecting Clifford parallel geodesics, such that only one hexagonal great circle in each set passes through each vertex, and the 20 hexagons in each set reach all 120 vertices.[26]
The √1.𝚫 chords form 144 central pentagons, 6 of which cross at each vertex.[k] The √1.𝚫 chords run vertex-to-every-second-vertex in the same planes as the 72 decagons: two pentagons are inscribed in each decagon. The √1.𝚫 chords join vertices which are two √0.𝚫 edges apart on a geodesic great circle. The 720 √1.𝚫 chords occur in 360 parallel pairs, √2.𝚽 = φ apart.
The √2 chords form 450 central squares, 15 of which cross at each vertex (3 from each of the five 24-cells that meet at the vertex). The √2 chords join vertices which are three √0.𝚫 edges apart (and two √1 chords apart). There are 600 √2 chords, in 300 parallel pairs, √2 apart. The 450 great squares (225 completely orthogonal pairs) can be divided into 15 sets of 30 non-intersecting Clifford parallel geodesics, such that only one square great circle in each set passes through each vertex, and the 30 squares (15 completely orthogonal pairs) in each set reach all 120 vertices.[27]
The √2.𝚽 = φ chords form the legs of 720 central isosceles triangles (72 sets of 10 inscribed in each decagon), 6 of which cross at each vertex. The third edge (base) of each isosceles triangle is of length √3.𝚽. The √2.𝚽 chords run vertex-to-every-third-vertex in the same planes as the 72 decagons, joining vertices which are three √0.𝚫 edges apart on a geodesic great circle. There are 720 distinct √2.𝚽 chords, in 360 parallel pairs, √1.𝚫 apart.
The √3 chords form 400 equilateral central triangles (25 sets of 32, with each triangle in two sets), 10 of which cross at each vertex (4 from each of five 24-cells, with each triangle in two of the 24-cells). Each set of 32 triangles consists of the 96 √3 chords and 24 vertices of one of the 25 overlapping inscribed 24-cells. The √3 chords run vertex-to-every-second-vertex in the same planes as the 200 hexagons: two triangles are inscribed in each hexagon. The √3 chords join vertices which are four √0.𝚫 edges apart (and two √1 chords apart on a geodesic great circle). Each √3 chord is the long diameter of two cubic cells in the same 24-cell.[ah] There are 1200 √3 chords, in 600 parallel pairs, √1 apart.
The √3.𝚽 chords (the diagonals of the pentagons) form the legs of 720 central isosceles triangles (144 sets of 5 inscribed in each pentagon), 6 of which cross at each vertex. The third edge (base) of each isosceles triangle is an edge of the pentagon of length √1.𝚫, so these are golden triangles. The √3.𝚽 chords run vertex-to-every-fourth-vertex in the same planes as the 72 decagons, joining vertices which are four √0.𝚫 edges apart on a geodesic great circle. There are 720 distinct √3.𝚽 chords, in 360 parallel pairs, √0.𝚫 apart.
The √4 chords occur as 60 long diameters (75 sets of 4 orthogonal axes with each set comprising a 16-cell), the 120 long radii of the 600-cell. The √4 chords join opposite vertices which are five √0.𝚫 edges apart on a geodesic great circle. There are 25 distinct but overlapping sets of 12 diameters, each comprising one of the 25 inscribed 24-cells.[j] There are 75 distinct but overlapping sets of 4 orthogonal diameters, each comprising one of the 75 inscribed 16-cells.
The sum of the squared lengths[ai] of all these distinct chords of the 600-cell is 14,400 = 1202.[aj] These are all the central polygons through vertices, but the 600-cell does have one noteworthy great circle that does not pass through any vertices (a 0-gon).[an] Moreover, in 4-space there are geodesics on the 3-sphere which do not lie in central planes at all. There are geodesic shortest paths between two 600-cell vertices that are helical rather than simply circular; they correspond to isoclinic (diagonal) rotations rather than simple rotations.[ao]
All the geodesic polygons enumerated above lie in central planes of just three kinds, each characterized by a rotation angle: decagon planes (𝜋/5 apart), hexagon planes (𝜋/3 apart, also in the 25 inscribed 24-cells), and square planes (𝜋/2 apart, also in the 75 inscribed 16-cells and the 24-cells). These central planes of the 600-cell can be divided into 4 orthogonal central hyperplanes (3-spaces) each forming an icosidodecahedron. There are 450 great squares 90 degrees apart; 200 great hexagons 60 degrees apart; and 72 great decagons 36 degrees apart.[at] Each great square plane is completely orthogonal to another great square plane. Each great hexagon plane is completely orthogonal to a plane which intersects only two vertices (one √4 long diameter): a great digon plane.[au] Each great decagon plane is completely orthogonal to a plane which intersects no vertices: a great 0-gon plane.[al]
Fibrations of great circle polygons
[edit]Each set of similar great circle polygons (squares or hexagons or decagons) can be divided into bundles of non-intersecting Clifford parallel great circles (of 30 squares or 20 hexagons or 12 decagons).[af] Each fiber bundle of Clifford parallel great circles[ap] is a discrete Hopf fibration which fills the 600-cell, visiting all 120 vertices just once.[32] Each discrete Hopf fibration has its 3-dimensional base which is a distinct polyhedron that acts as a map or scale model of the fibration.[av] The great circle polygons in each bundle spiral around each other, delineating helical rings of face-bonded cells which nest into each other, pass through each other without intersecting in any cells and exactly fill the 600-cell with their disjoint cell sets. The different fiber bundles with their cell rings each fill the same space (the 600-cell) but their fibers run Clifford parallel in different "directions"; great circle polygons in different fibrations are not Clifford parallel.[33]
Decagons
[edit]
The fibrations of the 600-cell include 6 fibrations of its 72 great decagons: 6 fiber bundles of 12 great decagons.[ae] The 12 Clifford parallel decagons in each bundle are completely disjoint. Adjacent parallel decagons are spanned by edges of other great decagons.
Each fiber bundle[aq] delineates 20 helical rings of 30 tetrahedral cells each,[ad] with five rings nesting together around each decagon.[34] The Hopf map of this fibration is the icosahedron, where each of 12 vertices lifts to a great decagon, and each of 20 triangular faces lifts to a 30-cell ring.[av] Each tetrahedral cell occupies only one of the 20 cell rings in each of the 6 fibrations. The tetrahedral cell contributes each of its 6 edges to a decagon in a different fibration, but contributes that edge to five distinct cell rings in the fibration.[ac]
The 12 great circles and 30-cell rings of the 600-cell's 6 characteristic Hopf fibrations make the 600-cell a geometric configuration of 30 "points" and 12 "lines" written as 302125. It is called the Schläfli double six configuration after Ludwig Schläfli,[36] the Swiss mathematician who discovered the 600-cell and the complete set of regular polytopes in n dimensions.[37]
Hexagons
[edit]The fibrations of the 24-cell include 4 fibrations of its 16 great hexagons: 4 fiber bundles of 4 great hexagons. The 4 Clifford parallel hexagons in each bundle are completely disjoint. Adjacent parallel hexagons are spanned by edges of other great hexagons. Each fiber bundle delineates 4 helical rings of 6 octahedral cells each, with three rings nesting together around each hexagon. Each octahedral cell occupies only one cell ring in each of the 4 fibrations. The octahedral cell contributes 3 of its 12 edges to 3 different Clifford parallel hexagons in each fibration, but contributes each edge to three distinct cell rings in the fibration.
The 600-cell contains 25 24-cells, and can be seen (10 different ways) as a compound of 5 disjoint 24-cells.[k] It has 10 fibrations of its 200 great hexagons: 10 fiber bundles of 20 great hexagons. The 20 Clifford parallel hexagons in each bundle are completely disjoint. Adjacent parallel hexagons are spanned by edges of great decagons.[ar] Each fiber bundle delineates 20 helical rings of 6 octahedral cells each, with three rings nesting together around each hexagon. The Hopf map of this fibration is the dodecahedron, where the 20 vertices each lift to a bundle of great hexagons.[26] Each octahedral cell occupies only one of the 20 6-octahedron rings in each of the 10 fibrations. The 20 6-octahedron rings belong to 5 disjoint 24-cells of 4 6-octahedron rings each; each hexagonal fibration of the 600-cell consists of 5 disjoint 24-cells.
Squares
[edit]The fibrations of the 16-cell include 3 fibrations of its 6 great squares: 3 fiber bundles of 2 great squares. The 2 Clifford parallel squares in each bundle are completely disjoint. Adjacent parallel squares are spanned by edges of other great squares. Each fiber bundle delineates 2 helical rings of 8 tetrahedral cells each. Each tetrahedral cell occupies only one cell ring in each of the 3 fibrations. The tetrahedral cell contributes each of its 6 edges to a different square (contributing two opposite non-intersecting edges to each of the 3 fibrations), but contributes each edge to both of the two distinct cell rings in the fibration.
The 600-cell contains 75 16-cells, and can be seen (10 different ways) as a compound of 15 disjoint 16-cells. It has 15 fibrations of its 450 great squares: 15 fiber bundles of 30 great squares. The 30 Clifford parallel squares in each bundle are completely disjoint. Adjacent parallel squares are spanned by edges of great decagons.[as] Each fiber bundle delineates 30 cell-disjoint helical rings of 8 tetrahedral cells each.[ax] The Hopf map of this fibration is the icosidodecahedron, where the 30 vertices each lift to a bundle of great squares.[27] Each tetrahedral cell occupies only one of the 30 8-tetrahedron rings in each of the 15 fibrations.
Clifford parallel cell rings
[edit]The densely packed helical cell rings[38][39][32] of fibrations are cell-disjoint, but they share vertices, edges and faces. Each fibration of the 600-cell can be seen as a dense packing of cell rings with the corresponding faces of adjacent cell rings face-bonded to each other.[ba] The same fibration can also be seen as a minimal sparse arrangement of fewer completely disjoint cell rings that do not touch at all.[g]
The fibrations of great decagons can be seen (five different ways) as 4 completely disjoint 30-cell rings with spaces separating them, rather than as 20 face-bonded cell rings, by leaving out all but one cell ring of the five that meet at each decagon.[40] The five different ways you can do this are equivalent, in that all five correspond to the same discrete fibration (in the same sense that the 6 decagonal fibrations are equivalent, in that all 6 cover the same 600-cell). The 4 cell rings still constitute the complete fibration: they include all 12 Clifford parallel decagons, which visit all 120 vertices.[bb] This subset of 4 of 20 cell rings is dimensionally analogous[bc] to the subset of 12 of 72 decagons, in that both are sets of completely disjoint Clifford parallel polytopes which visit all 120 vertices.[bd] The subset of 4 of 20 cell rings is one of 5 fibrations within the fibration of 12 of 72 decagons: a fibration of a fibration. All the fibrations have this two level structure with subfibrations.
The fibrations of the 24-cell's great hexagons can be seen (three different ways) as 2 completely disjoint 6-cell rings with spaces separating them, rather than as 4 face-bonded cell rings, by leaving out all but one cell ring of the three that meet at each hexagon. Therefore each of the 10 fibrations of the 600-cell's great hexagons can be seen as 2 completely disjoint octahedral cell rings.
The fibrations of the 16-cell's great squares can be seen (two different ways) as a single 8-tetrahedral-cell ring with an adjacent cell-ring-sized empty space, rather than as 2 face-bonded cell rings, by leaving out one of the two cell rings that meet at each square. Therefore each of the 15 fibrations of the 600-cell's great squares can be seen as a single tetrahedral cell ring.[ax]
The sparse constructions of the 600-cell's fibrations correspond to lower-symmetry decompositions of the 600-cell, 24-cell or 16-cell with cells of different colors to distinguish the cell rings from the spaces between them.[be] The particular lower-symmetry form of the 600-cell corresponding to the sparse construction of the great decagon fibrations is dimensionally analogous[bc] to the snub tetrahedron form of the icosahedron (which is the base[av] of these fibrations on the 2-sphere). Each of the 20 Boerdijk-Coxeter cell rings[ad] is lifted from a corresponding face of the icosahedron.[bh]
Constructions
[edit]The 600-cell incorporates the geometries of every convex regular polytope in the first four dimensions, except the 5-cell, the 120-cell, and the polygons {7} and above.[44] Consequently, there are numerous ways to construct or deconstruct the 600-cell, but none of them are trivial. The construction of the 600-cell from its regular predecessor the 24-cell can be difficult to visualize.
Gosset's construction
[edit]Thorold Gosset discovered the semiregular 4-polytopes, including the snub 24-cell with 96 vertices, which falls between the 24-cell and the 600-cell in the sequence of convex 4-polytopes of increasing size and complexity in the same radius. Gosset's construction of the 600-cell from the 24-cell is in two steps, using the snub 24-cell as an intermediate form. In the first, more complex step (described elsewhere) the snub 24-cell is constructed by a special snub truncation of a 24-cell at the golden sections of its edges.[9] In the second step the 600-cell is constructed in a straightforward manner by adding 4-pyramids (vertices) to facets of the snub 24-cell.[45]
The snub 24-cell is a diminished 600-cell from which 24 vertices (and the cluster of 20 tetrahedral cells around each) have been truncated,[u] leaving a "flat" icosahedral cell in place of each removed icosahedral pyramid.[p] The snub 24-cell thus has 24 icosahedral cells and the remaining 120 tetrahedral cells. The second step of Gosset's construction of the 600-cell is simply the reverse of this diminishing: an icosahedral pyramid of 20 tetrahedral cells is placed on each icosahedral cell.
Constructing the unit-radius 600-cell from its precursor the unit-radius 24-cell by Gosset's method actually requires three steps. The 24-cell precursor to the snub-24 cell is not of the same radius: it is larger, since the snub-24 cell is its truncation. Starting with the unit-radius 24-cell, the first step is to reciprocate it around its midsphere to construct its outer canonical dual: a larger 24-cell, since the 24-cell is self-dual. That larger 24-cell can then be snub truncated into a unit-radius snub 24-cell.
Cell clusters
[edit]Since it is so indirect, Gosset's construction may not help us very much to directly visualize how the 600 tetrahedral cells fit together into a curved 3-dimensional surface envelope,[v] or how they lie on the underlying surface envelope of the 24-cell's octahedral cells. For that it is helpful to build up the 600-cell directly from clusters of tetrahedral cells.
Most of us have difficulty visualizing the 600-cell from the outside in 4-space, or recognizing an outside view of the 600-cell due to our total lack of sensory experience in 4-dimensional spaces,[46] but we should be able to visualize the surface envelope of 600 cells from the inside because that volume is a 3-dimensional space that we could actually "walk around in" and explore.[47] In these exercises of building the 600-cell up from cell clusters, we are entirely within a 3-dimensional space, albeit a strangely small, closed curved space, in which we can go a mere ten edge lengths away in a straight line in any direction and return to our starting point.
Icosahedra
[edit]

The vertex figure of the 600-cell is the icosahedron.[p] Twenty tetrahedral cells meet at each vertex, forming an icosahedral pyramid whose apex is the vertex, surrounded by its base icosahedron. The 600-cell has a dihedral angle of 𝜋/3 + arccos(−1/4) ≈ 164.4775°.[49]
An entire 600-cell can be assembled from 24 such icosahedral pyramids (bonded face-to-face at 8 of the 20 faces of the icosahedron, colored yellow in the illustration), plus 24 clusters of 5 tetrahedral cells (four cells face-bonded around one) which fill the voids remaining between the icosahedra. Each icosahedron is face-bonded to each adjacent cluster of 5 cells by two blue faces that share an edge (which is also one of the six edges of the central tetrahedron of the five). Six clusters of 5 cells surround each icosahedron, and six icosahedra surround each cluster of 5 cells. Five tetrahedral cells surround each icosahedron edge: two from inside the icosahedral pyramid, and three from outside it.[bl]
The apexes of the 24 icosahedral pyramids are the vertices of a 24-cell inscribed in the 600-cell. The other 96 vertices (the vertices of the icosahedra) are the vertices of an inscribed snub 24-cell, which has exactly the same structure of icosahedra and tetrahedra described here, except that the icosahedra are not 4-pyramids filled by tetrahedral cells; they are only "flat" 3-dimensional icosahedral cells, because the central apical vertex is missing.
The 24-cell edges joining icosahedral pyramid apex vertices run through the centers of the yellow faces. Coloring the icosahedra with 8 yellow and 12 blue faces can be done in 5 distinct ways.[bm] Thus each icosahedral pyramid's apex vertex is a vertex of 5 distinct 24-cells,[i] and the 120 vertices comprise 25 (not 5) 24-cells.[f]
The icosahedra are face-bonded into geodesic "straight lines" by their opposite yellow faces, bent in the fourth dimension into a ring of 6 icosahedral pyramids. Their apexes are the vertices of a great circle hexagon. This hexagonal geodesic traverses a ring of 12 tetrahedral cells, alternately bonded face-to-face and vertex-to-vertex. The long diameter of each face-bonded pair of tetrahedra (each triangular bipyramid) is a hexagon edge (a 24-cell edge). There are 4 rings of 6 icosahedral pyramids intersecting at each apex-vertex, just as there are 4 cell-disjoint interlocking rings of 6 octahedra in the 24-cell (a hexagonal fibration).[bq]
The tetrahedral cells are face-bonded into triple helices, bent in the fourth dimension into rings of 30 tetrahedral cells.[ad] The three helices are geodesic "straight lines" of 10 edges: great circle decagons which run Clifford parallel[af] to each other. Each tetrahedron, having six edges, participates in six different decagons[ac] and thereby in all 6 of the decagonal fibrations of the 600-cell.
The partitioning of the 600-cell into clusters of 20 cells and clusters of 5 cells is artificial, since all the cells are the same. One can begin by picking out an icosahedral pyramid cluster centered at any arbitrarily chosen vertex, so there are 120 overlapping icosahedra in the 600-cell.[bj] Their 120 apexes are each a vertex of five 24-vertex 24-cells, so there are 5*120/24 = 25 overlapping 24-cells.[k]
Octahedra
[edit]There is another useful way to partition the 600-cell surface, into 24 clusters of 25 tetrahedral cells, which reveals more structure[55] and a direct construction of the 600-cell from its predecessor the 24-cell.
Begin with any one of the clusters of 5 cells (above), and consider its central cell to be the center object of a new larger cluster of tetrahedral cells. The central cell is the first section of the 600-cell beginning with a cell. By surrounding it with more tetrahedral cells, we can reach the deeper sections beginning with a cell.
First, note that a cluster of 5 cells consists of 4 overlapping pairs of face-bonded tetrahedra (triangular dipyramids) whose long diameter is a 24-cell edge (a hexagon edge) of length √1. Six more triangular dipyramids fit into the concavities on the surface of the cluster of 5,[br] so the exterior chords connecting its 4 apical vertices are also 24-cell edges of length √1. They form a tetrahedron of edge length √1, which is the second section of the 600-cell beginning with a cell.[bs] There are 600 of these √1 tetrahedral sections in the 600-cell.
With the six triangular dipyamids fit into the concavities, there are 12 new cells and 6 new vertices in addition to the 5 cells and 8 vertices of the original cluster. The 6 new vertices form the third section of the 600-cell beginning with a cell, an octahedron of edge length √1, obviously the cell of a 24-cell.[bt] As partially filled so far (by 17 tetrahedral cells), this √1 octahedron has concave faces into which a short triangular pyramid fits; it has the same volume as a regular tetrahedral cell but an irregular tetrahedral shape.[bu] Each octahedron surrounds 1 + 4 + 12 + 8 = 25 tetrahedral cells: 17 regular tetrahedral cells plus 8 volumetrically equivalent tetrahedral cells each consisting of 6 one-sixth fragments from 6 different regular tetrahedral cells that each span three adjacent octahedral cells.[bv]
Thus the unit-radius 600-cell may be constructed directly from its predecessor,[ab] the unit-radius 24-cell, by placing on each of its octahedral facets a truncated[bw] irregular octahedral pyramid of 14 vertices[bx] constructed (in the above manner) from 25 regular tetrahedral cells of edge length 1/φ ≈ 0.618.
Union of two tori
[edit]There is yet another useful way to partition the 600-cell surface into clusters of tetrahedral cells, which reveals more structure[56] and the decagonal fibrations of the 600-cell. An entire 600-cell can be assembled around two rings of 5 icosahedral pyramids, bonded vertex-to-vertex into two geodesic "straight lines".

The 120-cell can be decomposed into two disjoint tori. Since it is the dual of the 600-cell, this same dual tori structure exists in the 600-cell, although it is somewhat more complex. The 10-cell geodesic path in the 120-cell corresponds to the 10-vertex decagon path in the 600-cell.[57]
Start by assembling five tetrahedra around a common edge. This structure looks somewhat like an angular "flying saucer". Stack ten of these, vertex to vertex, "pancake" style. Fill in the annular ring between each pair of "flying saucers" with 10 tetrahedra to form an icosahedron. You can view this as five vertex-stacked icosahedral pyramids, with the five extra annular ring gaps also filled in.[bz] The surface is the same as that of ten stacked pentagonal antiprisms: a triangular-faced column with a pentagonal cross-section.[58] Bent into a columnar ring this is a torus consisting of 150 cells, ten edges long, with 100 exposed triangular faces,[ca] 150 exposed edges, and 50 exposed vertices. Stack another tetrahedron on each exposed face. This will give you a somewhat bumpy torus of 250 cells with 50 raised vertices, 50 valley vertices, and 100 valley edges.[cb] The valleys are 10 edge long closed paths and correspond to other instances of the 10-vertex decagon path mentioned above (great circle decagons). These decagons spiral around the center core decagon,[cc] but mathematically they are all equivalent (they all lie in central planes).
Build a second identical torus of 250 cells that interlinks with the first. This accounts for 500 cells. These two tori mate together with the valley vertices touching the raised vertices, leaving 100 tetrahedral voids that are filled with the remaining 100 tetrahedra that mate at the valley edges. This latter set of 100 tetrahedra are on the exact boundary of the duocylinder and form a Clifford torus.[cd] They can be "unrolled" into a square 10×10 array. Incidentally this structure forms one tetrahedral layer in the tetrahedral-octahedral honeycomb. There are exactly 50 "egg crate" recesses and peaks on both sides that mate with the 250 cell tori.[by] In this case into each recess, instead of an octahedron as in the honeycomb, fits a triangular bipyramid composed of two tetrahedra.
This decomposition of the 600-cell has symmetry [[10,2+,10]], order 400, the same symmetry as the grand antiprism.[59] The grand antiprism is just the 600-cell with the two above 150-cell tori removed, leaving only the single middle layer of 300 tetrahedra, dimensionally analogous[bc] to the 10-face belt of an icosahedron with the 5 top and 5 bottom faces removed (a pentagonal antiprism).[ce]
The two 150-cell tori each contain 6 Clifford parallel great decagons (five around one), and the two tori are Clifford parallel to each other, so together they constitute a complete fibration of 12 decagons that reaches all 120 vertices, despite filling only half the 600-cell with cells.
Boerdijk–Coxeter helix rings
[edit]The 600-cell can also be partitioned into 20 cell-disjoint intertwining rings of 30 cells,[34] each ten edges long, forming a discrete Hopf fibration which fills the entire 600-cell.[60][61] Each ring of 30 face-bonded tetrahedra is a cylindrical Boerdijk–Coxeter helix bent into a ring in the fourth dimension.
 A single 30-tetrahedron Boerdijk–Coxeter helix ring within the 600-cell, seen in stereographic projection.[ad] |  A 30-tetrahedron ring can be seen along the perimeter of this 30-gonal orthogonal projection of the 600-cell.[an] |  The 30-cell ring as a {30/11} polygram of 30 edges wound into a helix that twists around its axis 11 times. This projection along the axis of the 30-cell cylinder shows the 30 vertices 12° apart around the cylinder's circular cross section, with the edges connecting every 11th vertex on the circle.[am] |
 The 30-vertex, 30-tetrahedron Boerdijk–Coxeter helix ring, cut and laid out flat in 3-dimensional space. Three cyan Clifford parallel great decagons bound the ring.[ae] They are bridged by a skew 30-gram helix of 30 magenta edges linking all 30 vertices: the Petrie polygon of the 600-cell.[cf] The 15 orange edges and 15 yellow edges form separate 15-gram helices, the edge-paths of isoclines. | ||
The 30-cell ring is the 3-dimensional space occupied by the 30 vertices of three cyan Clifford parallel great decagons that lie adjacent to each other, 36° = 𝜋/5 = one 600-cell edge length apart at all their vertex pairs.[cg] The 30 magenta edges joining these vertex pairs form a helical triacontagram, a skew 30-gram spiral of 30 edge-bonded triangular faces, that is the Petrie polygon of the 600-cell.[cf] The dual of the 30-cell ring (the skew 30-gon made by connecting its cell centers) is the Petrie polygon of the 120-cell, the 600-cell's dual polytope.[aw] The central axis of the 30-cell ring is a great 30-gon geodesic that passes through the center of 30 faces, but does not intersect any vertices.[an]
The 15 orange edges and 15 yellow edges form separate 15-gram helices. Each orange or yellow edge crosses between two cyan great decagons. Successive orange or yellow edges of these 15-gram helices do not lie on the same great circle; they lie in different central planes inclined at 36° = 𝝅/5 to each other.[at] Each 15-gram helix is noteworthy as the edge-path of an isocline, the geodesic path of an isoclinic rotation.[ao] The isocline is a circular curve which intersects every second vertex of the 15-gram, missing the vertex in between. A single isocline runs twice around each orange (or yellow) 15-gram through every other vertex, hitting half the vertices on the first loop and the other half of them on the second loop. The two connected loops forms a single Möbius loop, a skew {15/2} pentadecagram. The pentadecagram is not shown in these illustrations (but see below), because its edges are invisible chords between vertices which are two orange (or two yellow) edges apart, and no chords are shown in these illustrations. Although the 30 vertices of the 30-cell ring do not lie in one great 30-gon central plane,[cg] these invisible pentadecagram isoclines are true geodesic circles of a special kind, that wind through all four dimensions rather than lying in a 2-dimensional plane as an ordinary geodesic great circle does.[ch]
Five of these 30-cell helices nest together and spiral around each of the 10-vertex decagon paths, forming the 150-cell torus described in the grand antiprism decomposition above.[59] Thus every great decagon is the center core decagon of a 150-cell torus.[ci] The 600-cell may be decomposed into 20 30-cell rings, or into two 150-cell tori and 10 30-cell rings, but not into four 150-cell tori of this kind.[cj] The 600-cell can be decomposed into four 150-cell tori of a different kind.[40]
Radial golden triangles
[edit]The 600-cell can be constructed radially from 720 golden triangles of edge lengths √0.𝚫 √1 √1 which meet at the center of the 4-polytope, each contributing two √1 radii and a √0.𝚫 edge. They form 1200 triangular pyramids with their apexes at the center: irregular tetrahedra with equilateral √0.𝚫 bases (the faces of the 600-cell). These form 600 tetrahedral pyramids with their apexes at the center: irregular 5-cells with regular √0.𝚫 tetrahedron bases (the cells of the 600-cell).
Characteristic orthoscheme
[edit]| Characteristics of the 600-cell[63] | |||||
|---|---|---|---|---|---|
| edge[64] | arc | dihedral[65] | |||
| 𝒍 | 36° | 164°29′ | |||
| 𝟀 | 22°15′20″ | 60° | |||
| 𝝉[ck] | 18° | 36° | |||
| 𝟁 | 17°44′40″ | 60° | |||
| 22°15′20″ | 90° | ||||
| 18° | 90° | ||||
| 17°44′40″ | 90° | ||||
| 37°44′40″ | |||||
Every regular 4-polytope has its characteristic 4-orthoscheme, an irregular 5-cell.[x] The characteristic 5-cell of the regular 600-cell is represented by the Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() , which can be read as a list of the dihedral angles between its mirror facets. It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron. The regular 600-cell is subdivided by its symmetry hyperplanes into 14400 instances of its characteristic 5-cell that all meet at its center.[ay]
, which can be read as a list of the dihedral angles between its mirror facets. It is an irregular tetrahedral pyramid based on the characteristic tetrahedron of the regular tetrahedron. The regular 600-cell is subdivided by its symmetry hyperplanes into 14400 instances of its characteristic 5-cell that all meet at its center.[ay]
The characteristic 5-cell (4-orthoscheme) has four more edges than its base characteristic tetrahedron (3-orthoscheme), joining the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 600-cell).[cl] If the regular 600-cell has unit radius and edge length , its characteristic 5-cell's ten edges have lengths , , around its exterior right-triangle face (the edges opposite the characteristic angles 𝟀, 𝝉, 𝟁),[ck] plus , , (the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the characteristic radii of the regular tetrahedron), plus , , , (edges which are the characteristic radii of the 600-cell). The 4-edge path along orthogonal edges of the orthoscheme is , , , , first from a 600-cell vertex to a 600-cell edge center, then turning 90° to a 600-cell face center, then turning 90° to a 600-cell tetrahedral cell center, then turning 90° to the 600-cell center.
Reflections
[edit]The 600-cell can be constructed by the reflections of its characteristic 5-cell in its own facets (its tetrahedral mirror walls).[cm] Reflections and rotations are related: a reflection in an even number of intersecting mirrors is a rotation.[67][68] For example, a full isoclinic rotation of the 600-cell in decagonal invariant planes takes each of the 120 vertices through 15 vertices and back to itself, on a skew pentadecagram2 geodesic isocline of circumference 5𝝅 that winds around the 3-sphere, as each great decagon rotates (like a wheel) and also tilts sideways (like a coin flipping) with the completely orthogonal plane.[cn] Any set of four orthogonal pairs of antipodal vertices (the 8 vertices of one of the 75 inscribed 16-cells)[bb] performing such an orbit visits 15 * 8 = 120 distinct vertices and generates the 600-cell sequentially in one full isoclinic rotation, just as any single characteristic 5-cell reflecting itself in its own mirror walls generates the 120 vertices simultaneously by reflection.[bo]
Weyl orbits
[edit]Another construction method uses quaternions and the Icosahedral symmetry of Weyl group orbits of order 120.[70] The following are the orbits of weights of D4 under the Weyl group W(D4):
- O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2}
- O(1000) : V1
- O(0010) : V2
- O(0001) : V3
With quaternions where is the conjugate of and and , then the Coxeter group is the symmetry group of the 600-cell and the 120-cell of order 14400.
Given such that and as an exchange of within , we can construct:
- the snub 24-cell
- the 600-cell
- the 120-cell
Rotations
[edit]The regular convex 4-polytopes are an expression of their underlying symmetry which is known as SO(4), the group of rotations[71] about a fixed point in 4-dimensional Euclidean space.[cx]
The 600-cell is generated by isoclinic rotations[ao] of the 24-cell by 36° = 𝜋/5 (the arc of one 600-cell edge length).[da]
Twenty-five 24-cells
[edit]There are 25 inscribed 24-cells in the 600-cell.[11][co] Therefore there are also 25 inscribed snub 24-cells, 75 inscribed tesseracts and 75 inscribed 16-cells.[f]
The 8-vertex 16-cell has 4 long diameters inclined at 90° = 𝜋/2 to each other, often taken as the 4 orthogonal axes or basis of the coordinate system.
The 24-vertex 24-cell has 12 long diameters inclined at 60° = 𝜋/3 to each other: 3 disjoint sets of 4 orthogonal axes, each set comprising the diameters of one of 3 inscribed 16-cells, isoclinically rotated by 𝜋/3 with respect to each other.[db]
The 120-vertex 600-cell has 60 long diameters: not just 5 disjoint sets of 12 diameters, each comprising one of 5 inscribed 24-cells (as we might suspect by analogy), but 25 distinct but overlapping sets of 12 diameters, each comprising one of 25 inscribed 24-cells.[76] There are 5 disjoint 24-cells in the 600-cell, but not just 5: there are 10 different ways to partition the 600-cell into 5 disjoint 24-cells.[j]
Like the 16-cells and 8-cells inscribed in the 24-cell, the 25 24-cells inscribed in the 600-cell are mutually isoclinic polytopes. The rotational distance between inscribed 24-cells is always 𝜋/5 in each invariant plane of rotation.[cy]
Five 24-cells are disjoint because they are Clifford parallel: their corresponding vertices are 𝜋/5 apart on two non-intersecting Clifford parallel[af] decagonal great circles (as well as 𝜋/5 apart on the same decagonal great circle).[ae] An isoclinic rotation of decagonal planes by 𝜋/5 takes each 24-cell to a disjoint 24-cell (just as an isoclinic rotation of hexagonal planes by 𝜋/3 takes each 16-cell to a disjoint 16-cell).[dc] Each isoclinic rotation occurs in two chiral forms: there are 4 disjoint 24-cells to the left of each 24-cell, and another 4 disjoint 24-cells to its right.[de] The left and right rotations reach different 24-cells; therefore each 24-cell belongs to two different sets of five disjoint 24-cells.
All Clifford parallel polytopes are isoclinic, but not all isoclinic polytopes are Clifford parallels (completely disjoint objects).[df] Each 24-cell is isoclinic and Clifford parallel to 8 others, and isoclinic but not Clifford parallel to 16 others.[d] With each of the 16 it shares 6 vertices: a hexagonal central plane.[i] Non-disjoint 24-cells are related by a simple rotation by 𝜋/5 in an invariant plane intersecting only two vertices of the 600-cell,[au] a rotation in which the completely orthogonal fixed plane is their common hexagonal central plane. They are also related by an isoclinic rotation in which both planes rotate by 𝜋/5.[dh]
There are two kinds of 𝜋/5 isoclinic rotations which take each 24-cell to another 24-cell.[dc] Disjoint 24-cells are related by a 𝜋/5 isoclinic rotation of an entire fibration of 12 Clifford parallel decagonal invariant planes. (There are 6 such sets of fibers, and a right or a left isoclinic rotation possible with each set, so there are 12 such distinct rotations.)[de] Non-disjoint 24-cells are related by a 𝜋/5 isoclinic rotation of an entire fibration of 20 Clifford parallel hexagonal invariant planes.[dj] (There are 10 such sets of fibers, so there are 20 such distinct rotations.)[dg]
On the other hand, each of the 10 sets of five disjoint 24-cells is Clifford parallel because its corresponding great hexagons are Clifford parallel. (24-cells do not have great decagons.) The 16 great hexagons in each 24-cell can be divided into 4 sets of 4 non-intersecting Clifford parallel geodesics, each set of which covers all 24 vertices of the 24-cell. The 200 great hexagons in the 600-cell can be divided into 10 sets of 20 non-intersecting Clifford parallel geodesics, each set of which covers all 120 vertices and constitutes a discrete hexagonal fibration. Each of the 10 sets of 20 disjoint hexagons can be divided into five sets of 4 disjoint hexagons, each set of 4 covering a disjoint 24-cell. Similarly, the corresponding great squares of disjoint 24-cells are Clifford parallel.
Rotations on polygram isoclines
[edit]The regular convex 4-polytopes each have their characteristic kind of right (and left) isoclinic rotation, corresponding to their characteristic kind of discrete Hopf fibration of great circles.[bg] For example, the 600-cell can be fibrated six different ways into a set of Clifford parallel great decagons, so the 600-cell has six distinct right (and left) isoclinic rotations in which those great decagon planes are invariant planes of rotation. We say these isoclinic rotations are characteristic of the 600-cell because the 600-cell's edges lie in their invariant planes. These rotations only emerge in the 600-cell, although they are also found in larger regular polytopes (the 120-cell) which contain inscribed instances of the 600-cell.
Just as the geodesic polygons (decagons or hexagons or squares) in the 600-cell's central planes form fiber bundles of Clifford parallel great circles, the corresponding geodesic skew polygrams (which trace the paths on the Clifford torus of vertices under isoclinic rotation)[79] form fiber bundles of Clifford parallel isoclines: helical circles which wind through all four dimensions.[ao] Since isoclinic rotations are chiral, occurring in left-handed and right-handed forms, each polygon fiber bundle has corresponding left and right polygram fiber bundles.[80] All the fiber bundles are aspects of the same discrete Hopf fibration, because the fibration is the various expressions of the same distinct left-right pair of isoclinic rotations.
Cell rings are another expression of the Hopf fibration. Each discrete fibration has a set of cell-disjoint cell rings that tesselates the 4-polytope.[ba] The isoclines in each chiral bundle spiral around each other: they are axial geodesics of the rings of face-bonded cells. The Clifford parallel cell rings of the fibration nest into each other, pass through each other without intersecting in any cells, and exactly fill the 600-cell with their disjoint cell sets.
Isoclinic rotations rotate a rigid object's vertices along parallel paths, each vertex circling within two orthogonal moving great circles, the way a loom weaves a piece of fabric from two orthogonal sets of parallel fibers. A bundle of Clifford parallel great circle polygons and a corresponding bundle of Clifford parallel skew polygram isoclines are the warp and woof of the same distinct left or right isoclinic rotation, which takes Clifford parallel great circle polygons to each other, flipping them like coins and rotating them through a Clifford parallel set of central planes. Meanwhile, because the polygons are also rotating individually like wheels, vertices are displaced along helical Clifford parallel isoclines (the chords of which form the skew polygram), through vertices which lie in successive Clifford parallel polygons.[bf]
In the 600-cell, each family of isoclinic skew polygrams (moving vertex paths in the decagon {10}, hexagon {6}, or square {4} great polygon rotations) can be divided into bundles of non-intersecting Clifford parallel polygram isoclines.[81] The isocline bundles occur in pairs of left and right chirality; the isoclines in each rotation act as chiral objects, as does each distinct isoclinic rotation itself.[az] Each fibration contains an equal number of left and right isoclines, in two disjoint bundles, which trace the paths of the 600-cell's vertices during the fibration's left or right isoclinic rotation respectively. Each left or right fiber bundle of isoclines by itself constitutes a discrete Hopf fibration which fills the entire 600-cell, visiting all 120 vertices just once. It is a different bundle of fibers than the bundle of Clifford parallel polygon great circles, but the two fiber bundles describe the same discrete fibration because they enumerate those 120 vertices together in the same distinct right (or left) isoclinic rotation, by their intersection as a fabric of cross-woven parallel fibers.
Each isoclinic rotation involves pairs of completely orthogonal invariant central planes of rotation, which both rotate through the same angle. There are two ways they can do this: by both rotating in the "same" direction, or by rotating in "opposite" directions (according to the right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes). The right polygram and right isoclinic rotation conventionally correspond to invariant pairs rotating in the same direction; the left polygram and left isoclinic rotation correspond to pairs rotating in opposite directions.[78] Left and right isoclines are different paths that go to different places. In addition, each distinct isoclinic rotation (left or right) can be performed in a positive or negative direction along the circular parallel fibers.
A fiber bundle of Clifford parallel isoclines is the set of helical vertex circles described by a distinct left or right isoclinic rotation. Each moving vertex travels along an isocline contained within a (moving) cell ring. While the left and right isoclinic rotations each double-rotate the same set of Clifford parallel invariant planes of rotation, they step through different sets of great circle polygons because left and right isoclinic rotations hit alternate vertices of the great circle {2p} polygon (where p is a prime ≤ 5).[dl] The left and right rotation share the same Hopf bundle of {2p} polygon fibers, which is both a left and right bundle, but they have different bundles of {p} polygons[82] because the discrete fibers are opposing left and right {p} polygons inscribed in the {2p} polygon.[dm]
A simple rotation is direct and local, taking some vertices to adjacent vertices along great circles, and some central planes to other central planes within the same hyperplane. (The 600-cell has four orthogonal central hyperplanes, each of which is an icosidodecahedron.) In a simple rotation, there is just a single pair of completely orthogonal invariant central planes of rotation; it does not constitute a fibration.
An isoclinic rotation is diagonal and global, taking all the vertices to non-adjacent vertices (two or more edge-lengths away)[cq] along diagonal isoclines, and all the central plane polygons to Clifford parallel polygons (of the same kind). A left-right pair of isoclinic rotations constitutes a discrete fibration. All the Clifford parallel central planes of the fibration are invariant planes of rotation, separated by two equal angles and lying in different hyperplanes.[at] The diagonal isocline[cr] is a shorter route between the non-adjacent vertices than the multiple simple routes between them available along edges: it is the shortest route on the 3-sphere, the geodesic.
Decagons and pentadecagrams
[edit]The fibrations of the 600-cell include 6 fibrations of its 72 great decagons: 6 fiber bundles of 12 great decagons,[ae] each delineating 20 chiral cell rings of 30 tetrahedral cells each,[ad] with three great decagons bounding each cell ring, and five cell rings nesting together around each decagon. The 12 Clifford parallel decagons in each bundle are completely disjoint. Adjacent parallel decagons are spanned by edges of other great decagons.[aq] Each fibration corresponds to a distinct left (and right) isoclinic rotation of the 600-cell in 12 great decagon invariant planes on 5𝝅 isoclines.
The bundle of 12 Clifford parallel decagon fibers is divided into a bundle of 12 left pentagon fibers and a bundle of 12 right pentagon fibers, with each left-right pair of pentagons inscribed in a decagon.[83] 12 great polygons comprise a fiber bundle covering all 120 vertices in a discrete Hopf fibration. There are 20 cell-disjoint 30-cell rings in the fibration, but only 4 completely disjoint 30-cell rings.[g] The 600-cell has six such discrete decagonal fibrations, and each is the domain (container) of a unique left-right pair of isoclinic rotations (left and right fiber bundles of 12 great pentagons).[dn] Each great decagon belongs to just one fibration,[82] but each 30-cell ring belongs to 5 of the six fibrations (and is completely disjoint from 1 other fibration). The 600-cell contains 72 great decagons, divided among six fibrations, each of which is a set of 20 cell-disjoint 30-cell rings (4 completely disjoint 30-cell rings), but the 600-cell has only 20 distinct 30-cell rings altogether. Each 30-cell ring contains 3 of the 12 Clifford parallel decagons in each of 5 fibrations, and 30 of the 120 vertices.
In these decagonal isoclinic rotations, vertices travel along isoclines which follow the edges of hexagons,[26] advancing a pythagorean distance of one hexagon edge in each double 36°×36° rotational unit.[dj] In an isoclinic rotation, each successive hexagon edge travelled lies in a different great hexagon, so the isocline describes a skew polygram, not a polygon. In a 60°×60° isoclinic rotation (as in the 24-cell's characteristic hexagonal rotation, and below in the hexagonal rotations of the 600-cell) this polygram is a hexagram: the isoclinic rotation follows a 6-edge circular path, just as a simple hexagonal rotation does, although it takes two revolutions to enumerate all the vertices in it, because the isocline is a double loop through every other vertex, and its chords are √3 chords of the hexagon instead of √1 hexagon edges.[dq] But in the 600-cell's 36°×36° characteristic decagonal rotation, successive great hexagons are closer together and more numerous, and the isocline polygram formed by their 15 hexagon edges is a pentadecagram (15-gram).[cn] It is not only not the same period as the hexagon or the simple decagonal rotation, it is not even an integer multiple of the period of the hexagon, or the decagon, or either's simple rotation. Only the compound {30/4}=2{15/2} triacontagram (30-gram), which is two 15-grams rotating in parallel (a black and a white), is a multiple of them all, and so constitutes the rotational unit of the decagonal isoclinic rotation.[dl]
In the 30-cell ring, the non-adjacent vertices linked by isoclinic rotations are two edge-lengths apart, with three other vertices of the ring lying between them.[ds] The two non-adjacent vertices are linked by a √1 chord of the isocline which is a great hexagon edge (a 24-cell edge). The √1 chords of the 30-cell ring (without the √0.𝚫 600-cell edges) form a skew triacontagram{30/4}=2{15/2} which contains 2 disjoint {15/2} Möbius double loops, a left-right pair of pentadecagram2 isoclines. Each left (or right) bundle of 12 pentagon fibers is crossed by a left (or right) bundle of 8 Clifford parallel pentadecagram fibers. Each distinct 30-cell ring has 2 double-loop pentadecagram isoclines running through its even or odd (black or white) vertices respectively.[cu] The pentadecagram helices have no inherent chirality, but each acts as either a left or right isocline in any distinct isoclinic rotation.[dk] The 2 pentadecagram fibers belong to the left and right fiber bundles of 5 different fibrations.
At each vertex, there are six great decagons and six pentadecagram isoclines (six black or six white) that cross at the vertex.[dv] Eight pentadecagram isoclines (four black and four white) comprise a unique right (or left) fiber bundle of isoclines covering all 120 vertices in the distinct right (or left) isoclinic rotation. Each fibration has a unique left and right isoclinic rotation, and corresponding unique left and right fiber bundles of 12 pentagons and 8 pentadecagram isoclines. There are only 20 distinct black isoclines and 20 distinct white isoclines in the 600-cell. Each distinct isocline belongs to 5 fiber bundles.
| Three sets of 30-cell ring chords from the same orthogonal projection viewpoint | |||
|---|---|---|---|
| Pentadecagram {15/2} | Triacontagram {30/4}=2{15/2} | Triacontagram {30/6}=6{5} | |
| All edges are pentadecagram isocline chords of length √1, which are also great hexagon edges of 24-cells inscribed in the 600-cell. | Only great pentagon edges of length √1.𝚫 ≈ 1.176. | ||
 |  |  | |
| A single black (or white) isocline is a Möbius double loop skew pentadecagram {15/2} of circumference 5𝝅.[cn] The √1 chords are 24-cell edges (hexagon edges) from different inscribed 24-cells. These chords are invisible (not shown) in the 30-cell ring illustration, where they join opposite vertices of two face-bonded tetrahedral cells that are two orange edges apart or two yellow edges apart. | The 30-cell ring as a skew compound of two disjoint pentadecagram {15/2} isoclines (a black-white pair, shown here as orange-yellow).[cu] The √1 chords of the isoclines link every 4th vertex of the 30-cell ring in a straight chord under two orange edges or two yellow edges. The doubly-curved isocline is the geodesic (shortest path) between those vertices; they are also two edges apart by three different angled paths along the edges of the face-bonded tetrahedra. | Each pentadecagram isocline (at left) intersects all six great pentagons (above) in two or three vertices. The pentagons lie on flat 2𝝅 great circles in the decagon invariant planes of rotation. The pentadecagrams are not flat: they are helical 5𝝅 isocline circles whose 15 chords lie in successive great hexagon planes inclined at 𝝅/5 = 36° to each other. The isocline circle is said to be twisting either left or right with the rotation, but all such pentadecagrams are directly congruent, each acting as a left or right isocline in different fibrations. | |
| No 600-cell edges appear in these illustrations, only invisible interior chords of the 600-cell. In this article, they should all properly be drawn as dashed lines. | |||
Two 15-gram double-loop isoclines are axial to each 30-cell ring. The 30-cell rings are chiral; each fibration contains 10 right (clockwise-spiraling) rings and 10 left (counterclockwise spiraling) rings, but the two isoclines in each 3-cell ring are directly congruent.[cv] Each acts as a left (or right) isocline a left (or right) rotation, but has no inherent chirality.[dk] The fibration's 20 left and 20 right 15-grams altogether contain 120 disjoint open pentagrams (60 left and 60 right), the open ends of which are adjacent 600-cell vertices (one √0.𝚫 edge-length apart). The 30 chords joining the isocline's 30 vertices are √1 hexagon edges (24-cell edges), connecting 600-cell vertices which are two 600-cell √0.𝚫 edges apart on a decagon great circle. [cs] These isocline chords are both hexagon edges and pentagram edges.
The 20 Clifford parallel isoclines (30-cell ring axes) of each left (or right) isocline bundle do not intersect each other. Either distinct decagonal isoclinic rotation (left or right) rotates all 120 vertices (and all 600 cells), but pentadecagram isoclines and pentagons are connected such that vertices alternate as 60 black and 60 white vertices (and 300 black and 300 white cells), like the black and white squares of the chessboard.[du] In the course of the rotation, the vertices on a left (or right) isocline rotate within the same 15-vertex black (or white) isocline, and the cells rotate within the same black (or white) 30-cell ring.
Hexagons and hexagrams
[edit]
The fibrations of the 600-cell include 10 fibrations of its 200 great hexagons: 10 fiber bundles of 20 great hexagons. The 20 Clifford parallel hexagons in each bundle are completely disjoint. Adjacent parallel hexagons are spanned by edges of great decagons.[ar] Each fibration corresponds to a distinct left (and right) isoclinic rotation of the 600-cell in 20 great hexagon invariant planes on 4𝝅 isoclines.
Each fiber bundle delineates 20 disjoint directly congruent cell rings of 6 octahedral cells each, with three cell rings nesting together around each hexagon. The bundle of 20 Clifford parallel hexagon fibers is divided into a bundle of 20 black √3 great triangle fibers and a bundle of 20 white great triangle fibers, with a black and a white triangle inscribed in each hexagon and 6 black and 6 white triangles in each 6-octahedron ring. The black or white triangles are joined by three intersecting black or white isoclines, each of which is a special kind of helical great circle[dq] through the corresponding vertices in 10 Clifford parallel black (or white) great triangles. The 10 √1.𝚫 chords of each isocline form a skew decagram {10/3}, 10 great pentagon edges joined end-to-end in a helical loop, winding 3 times around the 600-cell through all four dimensions rather than lying flat in a central plane. Each pair of black and white isoclines (intersecting antipodal great hexagon vertices) forms a compound 20-gon icosagram {20/6}=2{10/3}.
Notice the relation between the 24-cell's characteristic rotation in great hexagon invariant planes (on hexagram isoclines), and the 600-cell's own version of the rotation of great hexagon planes (on decagram isoclines). They are exactly the same isoclinic rotation: they have the same isocline. They have different numbers of the same isocline, and the 600-cell's √1.𝚫 isocline chord is shorter than the 24-cell's √3 isocline chord because the isocline intersects more vertices in the 600-cell (10) than it does in the 24-cell (6), but both Clifford polygrams have a 4𝝅 circumference.[dp] They have different isocline polygrams only because the isocline curve intersects more vertices in the 600-cell than it does in the 24-cell.[dy]
Squares and octagrams
[edit]
The fibrations of the 600-cell include 15 fibrations of its 450 great squares: 15 fiber bundles of 30 great squares. The 30 Clifford parallel squares in each bundle are completely disjoint. Adjacent parallel squares are spanned by edges of great decagons.[as] Each fibration corresponds to a distinct left (and right) isoclinic rotation of the 600-cell in 30 great square invariant planes (15 completely orthogonal pairs) on 4𝝅 isoclines.
Each fiber bundle delineates 30 chiral cell rings of 8 tetrahedral cells each,[ax] with a left and right cell ring nesting together to fill each of the 15 disjoint 16-cells inscribed in the 600-cell. Axial to each 8-tetrahedron ring is a special kind of helical great circle, an isocline.[ao] In a left (or right) isoclinic rotation of the 600-cell in great square invariant planes, all the vertices circulate on one of 15 Clifford parallel isoclines.
The 30 Clifford parallel squares in each bundle are joined by four Clifford parallel 24-gram isoclines (one through each vertex), each of which intersects one vertex in 24 of the 30 squares, and all 24 vertices of just one of the 600-cell's 25 24-cells. Each isocline is a 24-gram circuit intersecting all 25 24-cells, 24 of them just once and one of them 24 times. The 24 vertices in each 24-gram isocline comprise a unique 24-cell; there are 25 such distinct isoclines in the 600-cell. Each isocline is a skew {24/5} 24-gram, 24 φ = √2.𝚽 chords joined end-to-end in a helical loop, winding 5 times around one 24-cell through all four dimensions rather than lying flat in a central plane. Adjacent vertices of the 24-cell are one √1 chord apart, and 5 φ chords apart on its isocline. A left (or right) isoclinic rotation through 720° takes each 24-cell to and through every other 24-cell.
Notice the relations between the 16-cell's rotation of just 2 invariant great square planes, the 24-cell's rotation in 6 Clifford parallel great squares, and this rotation of the 600-cell in 30 Clifford parallel great squares. These three rotations are the same rotation, taking place on exactly the same kind of isocline circles, which happen to intersect more vertices in the 600-cell (24) than they do in the 16-cell (8).[dz] In the 16-cell's rotation the distance between vertices on an isocline curve is the √4 diameter. In the 600-cell vertices are closer together, and its √2.𝚽 = φ chord is the distance between adjacent vertices on the same isocline, but all these isoclines have a 4𝝅 circumference.
As a configuration
[edit]This configuration matrix[87] represents the 600-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 600-cell. The non-diagonal numbers say how many of the column's element occur in or at the row's element.
Here is the configuration expanded with k-face elements and k-figures. The diagonal element counts are the ratio of the full Coxeter group order, 14400, divided by the order of the subgroup with mirror removal.
| H4 | k-face | fk | f0 | f1 | f2 | f3 | k-fig | Notes | |
|---|---|---|---|---|---|---|---|---|---|
| H3 | ( ) | f0 | 120 | 12 | 30 | 20 | {3,5} | H4/H3 = 14400/120 = 120 | |
| A1H2 | { } | f1 | 2 | 720 | 5 | 5 | {5} | H4/H2A1 = 14400/10/2 = 720 | |
| A2A1 | {3} | f2 | 3 | 3 | 1200 | 2 | { } | H4/A2A1 = 14400/6/2 = 1200 | |
| A3 | {3,3} | f3 | 4 | 6 | 4 | 600 | ( ) | H4/A3 = 14400/24 = 600 |
Symmetries
[edit]The icosians are a specific set of Hamiltonian quaternions with the same symmetry as the 600-cell.[88] The icosians lie in the golden field, (a + b√5) + (c + d√5)i + (e + f√5)j + (g + h√5)k, where the eight variables are rational numbers.[89] The finite sums of the 120 unit icosians are called the icosian ring.
When interpreted as quaternions,[b] the 120 vertices of the 600-cell form a group under quaternionic multiplication. This group is often called the binary icosahedral group and denoted by 2I as it is the double cover of the ordinary icosahedral group I.[90] It occurs twice in the rotational symmetry group RSG of the 600-cell as an invariant subgroup, namely as the subgroup 2IL of quaternion left-multiplications and as the subgroup 2IR of quaternion right-multiplications. Each rotational symmetry of the 600-cell is generated by specific elements of 2IL and 2IR; the pair of opposite elements generate the same element of RSG. The centre of RSG consists of the non-rotation Id and the central inversion −Id. We have the isomorphism RSG ≅ (2IL × 2IR) / {Id, -Id}. The order of RSG equals 120 × 120/2 = 7200. The quaternion algebra as a tool for the treatment of 3D and 4D rotations, and as a road to the full understanding of the theory of rotations in 4-dimensional Euclidean space, is described by Mebius.[91]
The binary icosahedral group is isomorphic to SL(2,5).
The full symmetry group of the 600-cell is the Coxeter group H4.[92] This is a group of order 14400. It consists of 7200 rotations and 7200 rotation-reflections. The rotations form an invariant subgroup of the full symmetry group. The rotational symmetry group was first described by S.L. van Oss.[93] The H4 group and its Clifford algebra construction from 3-dimensional symmetry groups by induction is described by Dechant.[94]
Visualization
[edit]The symmetries of the 3-D surface of the 600-cell are somewhat difficult to visualize due to both the large number of tetrahedral cells,[v] and the fact that the tetrahedron has no opposing faces or vertices.[az] One can start by realizing the 600-cell is the dual of the 120-cell. One may also notice that the 600-cell also contains the vertices of a dodecahedron,[44] which with some effort can be seen in most of the below perspective projections.
2D projections
[edit]The H3 decagonal projection shows the plane of the van Oss polygon.
| H4 | - | F4 |
|---|---|---|
 [30] (Red=1) |  [20] (Red=1) |  [12] (Red=1) |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] (Red=1,orange=5,yellow=10) |  [6] (Red=1,orange=3,yellow=6) |  [4] (Red=1,orange=2,yellow=4) |
3D projections
[edit]A three-dimensional model of the 600-cell, in the collection of the Institut Henri Poincaré, was photographed in 1934–1935 by Man Ray, and formed part of two of his later "Shakesperean Equation" paintings.[95]
| Frame synchronized orthogonal isometric (left) and perspective (right) projections |
|---|
Diminished 600-cells
[edit]The snub 24-cell may be obtained from the 600-cell by removing the vertices of an inscribed 24-cell and taking the convex hull of the remaining vertices.[96] This process is a diminishing of the 600-cell.
The grand antiprism may be obtained by another diminishing of the 600-cell: removing 20 vertices that lie on two mutually orthogonal rings and taking the convex hull of the remaining vertices.[59]
A bi-24-diminished 600-cell, with all tridiminished icosahedron cells has 48 vertices removed, leaving 72 of 120 vertices of the 600-cell. The dual of a bi-24-diminished 600-cell, is a tri-24-diminished 600-cell, with 48 vertices and 72 hexahedron cells.
There are a total of 314,248,344 diminishings of the 600-cell by non-adjacent vertices. All of these consist of regular tetrahedral and icosahedral cells.[97]
| Diminished 600-cells | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Tri-24-diminished 600-cell | Bi-24-diminished 600-cell | Snub 24-cell (24-diminished 600-cell) | Grand antiprism (20-diminished 600-cell) | 600-cell | ||||||
| Vertices | 48 | 72 | 96 | 100 | 120 | ||||||
| Vertex figure (Symmetry) |  dual of tridiminished icosahedron ([3], order 6) |  tetragonal antiwedge ([2]+, order 2) |  tridiminished icosahedron ([3], order 6) |  bidiminished icosahedron ([2], order 4) |  Icosahedron ([5,3], order 120) | ||||||
| Symmetry | Order 144 (48×3 or 72×2) | [3+,4,3] Order 576 (96×6) | [10,2+,10] Order 400 (100×4) | [5,3,3] Order 14400 (120×120) | |||||||
| Net |  |  |  |  |  | ||||||
| Ortho H4 plane |  |  |  |  | |||||||
| Ortho F4 plane |  |  |  |  | |||||||
Related polytopes and honeycombs
[edit]The 600-cell is one of 15 regular and uniform polytopes with the same H4 symmetry [3,3,5]:[11]
| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-cell | rectified 120-cell | truncated 120-cell | cantellated 120-cell | runcinated 120-cell | cantitruncated 120-cell | runcitruncated 120-cell | omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||
 |  |  |  | 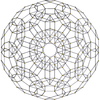 | 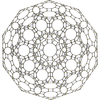 |  |  | ||||
 | 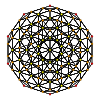 |  |  |  |  |  | |||||
| 600-cell | rectified 600-cell | truncated 600-cell | cantellated 600-cell | bitruncated 600-cell | cantitruncated 600-cell | runcitruncated 600-cell | omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
It is similar to three regular 4-polytopes: the 5-cell {3,3,3}, 16-cell {3,3,4} of Euclidean 4-space, and the order-6 tetrahedral honeycomb {3,3,6} of hyperbolic space. All of these have tetrahedral cells.
| {3,3,p} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||||||
| Form | Finite | Paracompact | Noncompact | ||||||||
| Name | {3,3,3} | {3,3,4} | {3,3,5} | {3,3,6} | {3,3,7} | {3,3,8} | ... {3,3,∞} | ||||
| Image |  |  |  |  |  |  |  | ||||
| Vertex figure |  {3,3} |  {3,4} |  {3,5} |  {3,6} |  {3,7} |  {3,8} |  {3,∞} | ||||
This 4-polytope is a part of a sequence of 4-polytope and honeycombs with icosahedron vertex figures:
| {p,3,5} polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||
| Form | Finite | Compact | Paracompact | Noncompact | |||
| Name | {3,3,5} | {4,3,5} | {5,3,5} | {6,3,5} | {7,3,5} | {8,3,5} | ... {∞,3,5} |
| Image |  |  |  |  |  |  |  |
| Cells | {3,3} | {4,3} | {5,3} | {6,3} | {7,3} | {8,3} | {∞,3} |
The regular complex polygons 3{5}3, ![]()
![]()
![]() and 5{3}5,
and 5{3}5, ![]()
![]()
![]() , in have a real representation as 600-cell in 4-dimensional space. Both have 120 vertices, and 120 edges. The first has Complex reflection group 3[5]3, order 360, and the second has symmetry 5[3]5, order 600.[98]
, in have a real representation as 600-cell in 4-dimensional space. Both have 120 vertices, and 120 edges. The first has Complex reflection group 3[5]3, order 360, and the second has symmetry 5[3]5, order 600.[98]
| Regular complex polytope in orthogonal projection of H4 Coxeter plane[17] | ||
|---|---|---|
 {3,3,5} Order 14400 |  3{5}3 Order 360 |  5{3}5 Order 600 |
See also
[edit]- 24-cell, the predecessor 4-polytope on which the 600-cell is based
- 120-cell, the dual 4-polytope to the 600-cell, and its successor
- Uniform 4-polytope family with [5,3,3] symmetry
- Regular 4-polytope
- Polytope
Notes
[edit]- ^ a b c The convex regular 4-polytopes can be ordered by size as a measure of 4-dimensional content (hypervolume) for the same radius. This is their proper order of enumeration, the order in which they nest inside each other as compounds.[3] Each greater polytope in the sequence is rounder than its predecessor, enclosing more content[4] within the same radius. The 4-simplex (5-cell) is the limit smallest case, and the 120-cell is the largest. Complexity (as measured by comparing configuration matrices or simply the number of vertices) follows the same ordering. This provides an alternative numerical naming scheme for regular polytopes in which the 600-cell is the 120-point 4-polytope: fifth in the ascending sequence that runs from 5-point 4-polytope to 600-point 4-polytope.
- ^ a b In four-dimensional Euclidean geometry, a quaternion is simply a (w, x, y, z) Cartesian coordinate.
- ^ a b c
Vertex geometry of the radially equilateral 24-cell, showing the 3 great circle polygons and the 4 vertex-to-vertex chord lengths. The 600-cell geometry is based on the 24-cell.
The 600-cell rounds out the 24-cell with 2 more great circle polygons (exterior decagon and interior pentagon), adding 4 more chord lengths which alternate with the 24-cell's 4 chord lengths. - ^ a b c d e f A 24-cell contains 16 hexagons. In the 600-cell, with 25 24-cells, each 24-cell is disjoint from 8 24-cells and intersects each of the other 16 24-cells in six vertices that form a hexagon.[12] A 600-cell contains 25・16/2 = 200 such hexagons.
- ^ In cases where inscribed 4-polytopes of the same kind occupy disjoint sets of vertices (such as the two 16-cells inscribed in the tesseract, or the three 16-cells inscribed in the 24-cell), their sets of vertex chords, central polygons and cells must likewise be disjoint. In the cases where they share vertices (such as the three tesseracts inscribed in the 24-cell, or the 25 24-cells inscribed in the 600-cell), they also share some vertex chords and central polygons.[d]
- ^ a b c d e The 600-cell contains exactly 25 24-cells, 75 16-cells and 75 8-cells, with each 16-cell and each 8-cell lying in just one 24-cell.[21]
- ^ a b c d e f g Polytopes are completely disjoint if all their element sets are disjoint: they do not share any vertices, edges, faces or cells. They may still overlap in space, sharing 4-content, volume, area, or lineage.
- ^ Each of the 25 24-cells of the 600-cell contains exactly one vertex of each great pentagon.[12] Six pentagons intersect at each 600-cell vertex, so each 24-cell intersects all 144 great pentagons.
- ^ a b c d e f Five 24-cells meet at each icosahedral pyramid apex[p] of the 600-cell. Each 24-cell shares not just one vertex but 6 vertices (one of its four hexagonal central planes) with each of the other four 24-cells.[d]
- ^ a b c Schoute was the first to state (a century ago) that there are exactly ten ways to partition the 120 vertices of the 600-cell into five disjoint 24-cells. The 25 24-cells can be placed in a 5 x 5 array such that each row and each column of the array partitions the 120 vertices of the 600-cell into five disjoint 24-cells. The rows and columns of the array are the only ten such partitions of the 600-cell.[21]
- ^ a b c d e The 600-cell contains 25 distinct 24-cells, bound to each other by pentagonal rings. Each pentagon links five completely disjoint[g] 24-cells together, the collective vertices of which are the 120 vertices of the 600-cell. Each 24-point 24-cell contains one fifth of all the vertices in the 120-point 600-cell, and is linked to the other 96 vertices (which comprise a snub 24-cell) by the 600-cell's 144 pentagons. Each of the 25 24-cells intersects each of the 144 great pentagons at just one vertex.[h] Five 24-cells meet at each 600-cell vertex,[i] so all 25 24-cells are linked by each great pentagon. The 600-cell can be partitioned into five disjoint 24-cells (10 different ways),[j] and also into 24 disjoint pentagons (inscribed in the 12 Clifford parallel great decagons of one of the 6 decagonal fibrations) by choosing a pentagon from the same fibration at each 24-cell vertex.
- ^ The angles 𝜉i and 𝜉j are angles of rotation in the two completely orthogonal invariant planes which characterize rotations in 4-dimensional Euclidean space. The angle 𝜂 is the inclination of both these planes from the polar axis, where 𝜂 ranges from 0 to 𝜋/2. The (𝜉i, 0, 𝜉j) coordinates describe the great circles which intersect at the north and south pole ("lines of longitude"). The (𝜉i, 𝜋/2, 𝜉j) coordinates describe the great circles orthogonal to longitude ("equators"); there is more than one "equator" great circle in a 4-polytope, as the equator of a 3-sphere is a whole 2-sphere of great circles. The other Hopf coordinates (𝜉i, 0 < 𝜂 < 𝜋/2, 𝜉j) describe the great circles (not "lines of latitude") which cross an equator but do not pass through the north or south pole.
- ^ The conversion from Hopf coordinates (𝜉i, 𝜂, 𝜉j) to unit-radius Cartesian coordinates (w, x, y, z) is:
- w = cos 𝜉i sin 𝜂
- x = cos 𝜉j cos 𝜂
- y = sin 𝜉j cos 𝜂
- z = sin 𝜉i sin 𝜂
- ^ The Hopf coordinates are triples of three angles:
- (𝜉i, 𝜂, 𝜉j)
- ^ There are 600 permutations of these coordinates, but there are only 120 vertices in the 600-cell. These are actually the Hopf coordinates of the vertices of the 120-cell, which has 600 vertices and can be seen (two different ways) as a compound of 5 disjoint 600-cells.
- ^ a b c d e f g h i In the curved 3-dimensional space of the 600-cell's boundary surface, at each vertex one finds the twelve nearest other vertices surrounding the vertex the way an icosahedron's vertices surround its center. Twelve 600-cell edges converge at the icosahedron's center, where they appear to form six straight lines which cross there. However, the center is actually displaced in the 4th dimension (radially outward from the center of the 600-cell), out of the hyperplane defined by the icosahedron's vertices. Thus the vertex icosahedron is actually a canonical icosahedral pyramid,[bj] composed of 20 regular tetrahedra on a regular icosahedron base, and the vertex is its apex.[bk]
- ^ a b c The fractional-root golden chords are irrational fractions that are functions of √5. They exemplify that the golden ratio φ = 1 + √5/2 ≈ 1.618 is a circle ratio related to 𝜋:[20]
- 𝜋/5 = arccos (φ/2)
- φ = 1 – 2 cos (3𝜋/5)
- ^ a b The 600-cell edges are decagon edges of length √0.𝚫, which is 𝚽, the smaller golden section of √5; the edges are in the inverse golden ratio 1/φ to the √1 hexagon chords (the 24-cell edges). The other fractional-root chords exhibit golden relationships as well. The chord of length √1.𝚫 is a pentagon edge. The next fractional-root chord is a decagon diagonal of length √2.𝚽 which is φ, the larger golden section of


 French
French Deutsch
Deutsch


































































![{\displaystyle [p,q]:r\rightarrow r'=prq}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a2020e8f2ccdbd85dea0af38e6a0127d5446e42)
![{\displaystyle [p,q]^{*}:r\rightarrow r''=p{\bar {r}}q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b3a23b7f4033871816e91c387a44cf392cac24bd)
![{\displaystyle W(H_{4})=\lbrace [p,{\bar {p}}]\oplus [p,{\bar {p}}]^{*}\rbrace }](https://wikimedia.org/api/rest_v1/media/math/render/svg/13545fc184e7fc37a87f7446d0b9e70bc07cf3b7)