File:SIR model anim.gif

Size of this preview: 760 × 600 pixels. Other resolutions: 304 × 240 pixels | 608 × 480 pixels | 973 × 768 pixels | 1,048 × 827 pixels.

Original file (1,048 × 827 pixels, file size: 4.62 MB, MIME type: image/gif, looped, 77 frames, 0.8 s)

This is a file from the Wikimedia Commons. Information from its description page there is shown below.
Commons is a freely licensed media file repository. You can help.

Summary

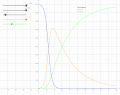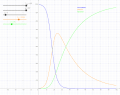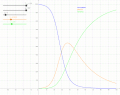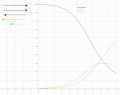
DescriptionSIR model anim.gif	Deutsch: Animation zum SIR-Modell mit den Startwerten $S(0)=997$ , $I(0)=3$ , $R(0)=0$ sowie anfänglicher Infektionsrate $\beta =0{,}0005$ sowie der konstanten Rate $\gamma =0{,}04$ für die Gruppe R. Stehen weder Medikamente noch eine Impfung zur Verfügung, so kann man nur die Zahl der Infektionen reduzieren (häufig als „Abflachung der Kurve“ bezeichnet), indem man geeignete Maßnahmen ergreift (z. B. durch weitgehende Kontaktvermeidung, Ausgangsperre). Die Animation zeigt, wie sich eine Senkung der Infektionsrate um 76 % (von $\beta =0{,}0005$ auf $\beta =0{,}00012$ ) auswirkt. System von Differentialgleichungen für dieses Modell: ${\frac {\mathrm {d} S}{\mathrm {d} t}}=-\beta \cdot S(t)\cdot I(t)$ ${\frac {\mathrm {d} I}{\mathrm {d} t}}=\beta \cdot S(t)\cdot I(t)-\gamma \cdot I(t)$ ${\frac {\mathrm {d} R}{\mathrm {d} t}}=\gamma \cdot I(t)$ Diese Animation wurde mit GeoGebra erstellt, wobei die numerischen Lösungen des genannten Systems der Differentialgleichungen ermittelt wurden. Der entscheidende Teil der Konstruktion lautet: ########################################## # das System der Differentialgleichungen # ########################################## S'(t, S, I, R) = -ß I S I'(t, S, I, R) = ß S I - γ I R'(t, S, I, R) = γ I ####################################################################### # numerische Lösung des Systems der Differentialgleichungen bestimmen # ####################################################################### NLöseDgl[{S', I', R'}, 0, {s_0, i_0, r_0}, T_{max}] # liefert: # NumerischesIntegral1 -> S # NumerischesIntegral2 -> I # NumerischesIntegral3 -> R Anmerkung: In der Literatur werden teilweise modifizierte Formen dieser Differentialgleichungen (DGL) benutzt, die aber gleichwertig sind. Leider werden oft dieselben Parameter benutzt. Beispiel für die erste DGL, wobei die Infektionsrate der Klarheit halber ${\tilde {\beta }}$ benannt ist: ${\frac {\mathrm {d} S}{\mathrm {d} t}}=-{\frac {\tilde {\beta }}{N}}\cdot S(t)\cdot I(t)$ Setzt man $\beta ={\tfrac {\tilde {\beta }}{N}}$ , so ist die DGL identisch mit der oben verwendeten. $N$ ist konstant (Invariante des Modells) und für die Aufstellung der DGL nicht erforderlich; bei der hier verwendeten Implementierung wurde noch nicht einmal eine Variable für $N$ vorgesehen. English: Animation of the SIR model with initial values $S(0)=997$ , $I(0)=3$ , $R(0)=0$ , and rate of recovery $\gamma =0.04$ . The animation shows the effect of reducing the rate of infection from $\beta =0.5$ to $\beta =0.12$ . If there is no medicine or vaccination available, it is only possible to reduce the infection rate (often referred to as "flattening the curve") by appropriate measures such as social distancing. System of differential equations used for this model: ${\frac {dS}{dt}}=-\beta \cdot S(t)\cdot I(t)$ ${\frac {dI}{dt}}=\beta \cdot S(t)\cdot I(t)-\gamma \cdot I(t)$ ${\frac {dR}{dt}}=\gamma \cdot I(t)$ This animation was created with GeoGebra by computing the numerical solutions of the system of differential equations. The core part of the construction is as follows: #################################### # system of differential equations # #################################### S'(t, S, I, R) = -ß I S I'(t, S, I, R) = ß S I - γ I R'(t, S, I, R) = γ I ############################################################### # numerical solutions of the system of differential equations # ############################################################### NSolveODE[{S', I', R'}, 0, {s_0, i_0, r_0}, T_{max}] # Result: # numericalIntegral1 -> S # numericalIntegral2 -> I # numericalIntegral3 -> R Note: Some authors use modified, but equivalent forms of the ODEs. Unfortunately, the same parameters are sometimes used. Example for the first ODE, where the infection rate is named ${\tilde {\beta }}$ for the sake of clarity: ${\frac {dS}{dt}}=-{\frac {\tilde {\beta }}{N}}\cdot S(t)\cdot I(t)$ By substituting $\beta ={\tfrac {\tilde {\beta }}{N}}$ , you get the same ODE as above. $N$ is a constant value (invariant of the model) and not needed for the ODE; in fact, the implementation didn't even use a variable for $N$ .
Date	18 March 2020
Source	own image
Author	Phrontis

Licensing

I, the copyright holder of this work, hereby publish it under the following license:

This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.

You are free:

to share – to copy, distribute and transmit the work
to remix – to adapt the work

Under the following conditions:

attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.

I have published this image or video as author Phrontis under the licence "CC-BY-SA-3.0" in Wikipedia. This means that free (non-commercial as well as commercial) usage outside of Wikipedia is permitted under the following licence terms: Online media: The author „Phrontis at Wikimedia Commons“ is named The license "Creative Commons Attribution ShareAlike 3.0" (short: cc-by-sa-3.0) is named. The name of the license (full or short) is linked to https://creativecommons.org/licenses/by-sa/3.0/ As alternative to the previous condition you may use a link to the original image: //commons.wikimedia.org/wiki/File:SIR_model_anim.gif Print media: The author „Phrontis at Wikimedia Commons“ is named The license "Creative Commons Attribution ShareAlike 3.0" (short: cc-by-sa-3.0) and the link https://creativecommons.org/licenses/by-sa/3.0 is named. Please send me a specimen copy or the URL of the website where the image or video is used. Please contact me via Wikipedia (email (account needed) or leave a message) if you need the image or video in a higher resolution need my postal address for sending a specimen copy have further questions about the terms of the licence.
Dieses Foto bzw. Video habe ich als Urheber Phrontis unter der Lizenz „CC-BY-SA-3.0 (de)“ in der Wikipedia veröffentlicht. Dies bedeutet, dass eine kostenlose – sowohl nichtkommerzielle als auch kommerzielle – Nutzung außerhalb der Wikipedia unter folgenden Bedingungen möglich ist: Online-Medien: Als Urheber wird „Phrontis auf Wikimedia Commons“ genannt. Es wird die Lizenz „Creative Commons Attribution ShareAlike 3.0“ (Kurzform: cc-by-sa-3.0) genannt und mit der URL https://creativecommons.org/licenses/by-sa/3.0/ verlinkt. Alternativ zum vorstehenden Punkt darf als Vereinfachung auch ein Link auf das Originalfoto gesetzt werden: //commons.wikimedia.org/wiki/File:SIR_model_anim.gif Print-Medien: Als Urheber wird „Phrontis auf Wikimedia Commons“ genannt. Es wird die Lizenz „Creative Commons Attribution ShareAlike 3.0“ (Kurzform: cc-by-sa-3.0) sowie der Link https://creativecommons.org/licenses/by-sa/3.0/ genannt. Ich bitte um Zusendung eines Belegexemplares bzw. der URL, wo das Foto bzw. das Video benutzt wird. Bitte kontaktieren Sie mich über Wikipedia (E-Mail (Benutzerkonto erforderlich) oder hinterlassen Sie eine Nachricht), wenn Sie das Foto bzw. Video in einer höheren Auflösung benötigen meine Adresse für die Zusendung eines Belegexemplares benötigen weitergehende Fragen zur Lizenznutzung haben.

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	09:52, 28 March 2020		1,048 × 827 (4.62 MB)	Phrontis	+loop
	12:47, 18 March 2020		1,048 × 827 (4.62 MB)	Phrontis	== {{int:filedesc}} == {{Information \|Description= {{de\|1=Animation zum SIR-Modell mit den Startwerten <math display="inline">S_0=997, I_0=3, R_0=0</math> sowie anfänglicher Infektionsrate <math display="inline">\beta=0,0005</math> sowie der konstanten Rate <math display="inline">\gamma=0,004</math> für die Gruppe ''R''. Stehen weder Medikamente noch eine Impfung zur Verfügung, so kann man nur die Zahl der Infektionen reduzieren (häufig als „Abflachung der Kurve“ bezeichnet), indem man geeig...