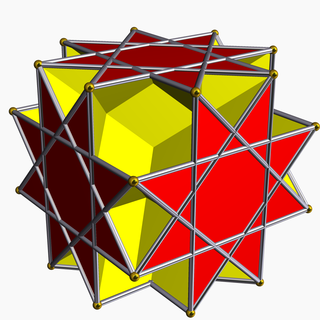
Great rhombihexahedron
| Great rhombihexahedron | |
|---|---|
 | |
| Type | Uniform star polyhedron |
| Elements | F = 18, E = 48 V = 24 (χ = −6) |
| Faces by sides | 12{4}+6{8/3} |
| Coxeter diagram | |
| Wythoff symbol | 2 4/3 (3/2 4/2) | |
| Symmetry group | Oh, [4,3], *432 |
| Index references | U21, C82, W103 |
| Dual polyhedron | Great rhombihexacron |
| Vertex figure |  4.8/3.4/3.8/5 |
| Bowers acronym | Groh |

In geometry, the great rhombihexahedron (or great rhombicube) is a nonconvex uniform polyhedron, indexed as U21. It has 18 faces (12 squares and 6 octagrams), 48 edges, and 24 vertices.[1] Its dual is the great rhombihexacron.[2] Its vertex figure is a crossed quadrilateral.
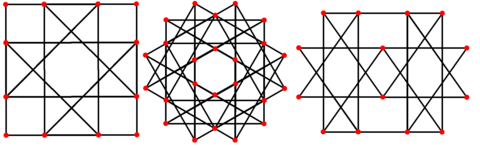
Orthogonal projections
[edit]Gallery
[edit]
 Traditional filling |  Modulo-2 filling |
Related polyhedra
[edit]It shares the vertex arrangement with the convex truncated cube. It additionally shares its edge arrangement with the nonconvex great rhombicuboctahedron (having 12 square faces in common), and with the great cubicuboctahedron (having the octagrammic faces in common).
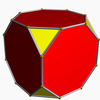 Truncated cube |  Nonconvex great rhombicuboctahedron |  Great cubicuboctahedron |  Great rhombihexahedron |
It may be constructed as the exclusive or (blend) of three octagrammic prisms. Similarly, the small rhombihexahedron may be constructed as the exclusive or of three octagonal prisms.
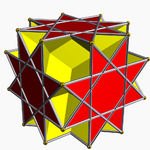
Great rhombihexacron
[edit]| Great rhombihexacron | |
|---|---|
 | |
| Type | Star polyhedron |
| Face |  |
| Elements | F = 24, E = 48 V = 18 (χ = −6) |
| Symmetry group | Oh, [4,3], *432 |
| Index references | DU21 |
| dual polyhedron | Great rhombihexahedron |

The great rhombihexacron is a nonconvex isohedral polyhedron. It is the dual of the uniform great rhombihexahedron (U21).[3] It has 24 identical bow-tie-shaped faces, 18 vertices, and 48 edges.
It has 12 outer vertices which have the same vertex arrangement as the cuboctahedron, and 6 inner vertices with the vertex arrangement of an octahedron.
As a surface geometry, it can be seen as visually similar to a Catalan solid, the disdyakis dodecahedron, with much taller rhombus-based pyramids joined to each face of a rhombic dodecahedron.
See also
[edit]References
[edit]- ^ Maeder, Roman. "21: great rhombihexahedron". MathConsult.
- ^ Weisstein, Eric W. "Great Rhombihexahedron". MathWorld.
- ^ Weisstein, Eric W. "Great rhombihexacron". MathWorld.
- Wenninger, Magnus (1983), Dual Models, Cambridge University Press, ISBN 978-0-521-54325-5, MR 0730208
- uniform polyhedra and duals
External links
[edit]


 French
French Deutsch
Deutsch