Theta function

In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory.^[1]

The most common form of theta function is that occurring in the theory of elliptic functions. With respect to one of the complex variables (conventionally called z), a theta function has a property expressing its behavior with respect to the addition of a period of the associated elliptic functions, making it a quasiperiodic function. In the abstract theory this quasiperiodicity comes from the cohomology class of a line bundle on a complex torus, a condition of descent.

One interpretation of theta functions when dealing with the heat equation is that "a theta function is a special function that describes the evolution of temperature on a segment domain subject to certain boundary conditions".^[2]

Throughout this article, ${\displaystyle (e^{\pi i\tau })^{\alpha }}$ should be interpreted as ${\displaystyle e^{\alpha \pi i\tau }}$ (in order to resolve issues of choice of branch).^{[note 1]}

There are several closely related functions called Jacobi theta functions, and many different and incompatible systems of notation for them. One Jacobi theta function (named after Carl Gustav Jacob Jacobi) is a function defined for two complex variables z and τ, where z can be any complex number and τ is the half-period ratio, confined to the upper half-plane, which means it has positive imaginary part. It is given by the formula

${\displaystyle {\begin{aligned}\vartheta (z;\tau )&=\sum _{n=-\infty }^{\infty }\exp \left(\pi in^{2}\tau +2\pi inz\right)\\&=1+2\sum _{n=1}^{\infty }q^{n^{2}}\cos(2\pi nz)\\&=\sum _{n=-\infty }^{\infty }q^{n^{2}}\eta ^{n}\end{aligned}}}$

where q = exp(πiτ) is the nome and η = exp(2πiz). It is a Jacobi form. The restriction ensures that it is an absolutely convergent series. At fixed τ, this is a Fourier series for a 1-periodic entire function of z. Accordingly, the theta function is 1-periodic in z:

${\displaystyle \vartheta (z+1;\tau )=\vartheta (z;\tau ).}$

By completing the square, it is also τ-quasiperiodic in z, with

${\displaystyle \vartheta (z+\tau ;\tau )=\exp {\bigl (}-\pi i(\tau +2z){\bigr )}\vartheta (z;\tau ).}$

Thus, in general,

${\displaystyle \vartheta (z+a+b\tau ;\tau )=\exp \left(-\pi ib^{2}\tau -2\pi ibz\right)\vartheta (z;\tau )}$

for any integers a and b.

For any fixed ${\displaystyle \tau }$, the function is an entire function on the complex plane, so by Liouville's theorem, it cannot be doubly periodic in ${\displaystyle 1,\tau }$ unless it is constant, and so the best we could do is to make it periodic in ${\displaystyle 1}$ and quasi-periodic in ${\displaystyle \tau }$. Indeed, since $${\displaystyle \left|{\frac {\vartheta (z+a+b\tau ;\tau )}{\vartheta (z;\tau )}}\right|=\exp \left(\pi (b^{2}\Im (\tau )+2b\Im (z))\right)}$$and ${\displaystyle \Im (\tau )>0}$, the function ${\displaystyle \vartheta (z,\tau )}$ is unbounded, as required by Liouville's theorem.

It is in fact the most general entire function with 2 quasi-periods, in the following sense:^[3]

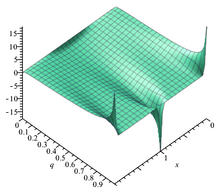
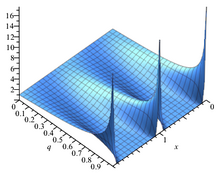
The Jacobi theta function defined above is sometimes considered along with three auxiliary theta functions, in which case it is written with a double 0 subscript:

${\displaystyle \vartheta _{00}(z;\tau )=\vartheta (z;\tau )}$

The auxiliary (or half-period) functions are defined by

${\displaystyle {\begin{aligned}\vartheta _{01}(z;\tau )&=\vartheta \left(z+{\tfrac {1}{2}};\tau \right)\\[3pt]\vartheta _{10}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi iz\right)\vartheta \left(z+{\tfrac {1}{2}}\tau ;\tau \right)\\[3pt]\vartheta _{11}(z;\tau )&=\exp \left({\tfrac {1}{4}}\pi i\tau +\pi i\left(z+{\tfrac {1}{2}}\right)\right)\vartheta \left(z+{\tfrac {1}{2}}\tau +{\tfrac {1}{2}};\tau \right).\end{aligned}}}$

This notation follows Riemann and Mumford; Jacobi's original formulation was in terms of the nome q = e^iπτ rather than τ. In Jacobi's notation the θ-functions are written:

${\displaystyle {\begin{aligned}\theta _{1}(z;q)&=\theta _{1}(\pi z,q)=-\vartheta _{11}(z;\tau )\\\theta _{2}(z;q)&=\theta _{2}(\pi z,q)=\vartheta _{10}(z;\tau )\\\theta _{3}(z;q)&=\theta _{3}(\pi z,q)=\vartheta _{00}(z;\tau )\\\theta _{4}(z;q)&=\theta _{4}(\pi z,q)=\vartheta _{01}(z;\tau )\end{aligned}}}$

The above definitions of the Jacobi theta functions are by no means unique. See Jacobi theta functions (notational variations) for further discussion.

If we set z = 0 in the above theta functions, we obtain four functions of τ only, defined on the upper half-plane. These functions are called Theta Nullwert functions, based on the German term for zero value because of the annullation of the left entry in the theta function expression. Alternatively, we obtain four functions of q only, defined on the unit disk ${\displaystyle |q|<1}$. They are sometimes called theta constants:^{[note 2]}

${\displaystyle {\begin{aligned}\vartheta _{11}(0;\tau )&=-\theta _{1}(q)=-\sum _{n=-\infty }^{\infty }(-1)^{n-1/2}q^{(n+1/2)^{2}}\\\vartheta _{10}(0;\tau )&=\theta _{2}(q)=\sum _{n=-\infty }^{\infty }q^{(n+1/2)^{2}}\\\vartheta _{00}(0;\tau )&=\theta _{3}(q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}\\\vartheta _{01}(0;\tau )&=\theta _{4}(q)=\sum _{n=-\infty }^{\infty }(-1)^{n}q^{n^{2}}\end{aligned}}}$

with the nome q = e^iπτ. Observe that ${\displaystyle \theta _{1}(q)=0}$. These can be used to define a variety of modular forms, and to parametrize certain curves; in particular, the Jacobi identity is

${\displaystyle \theta _{2}(q)^{4}+\theta _{4}(q)^{4}=\theta _{3}(q)^{4}}$

or equivalently,

${\displaystyle \vartheta _{01}(0;\tau )^{4}+\vartheta _{10}(0;\tau )^{4}=\vartheta _{00}(0;\tau )^{4}}$

which is the Fermat curve of degree four.

Jacobi's identities describe how theta functions transform under the modular group, which is generated by τ ↦ τ + 1 and τ ↦ −⁠1/τ⁠. Equations for the first transform are easily found since adding one to τ in the exponent has the same effect as adding ⁠1/2⁠ to z (n ≡ n² mod 2). For the second, let

${\displaystyle \alpha =(-i\tau )^{\frac {1}{2}}\exp \left({\frac {\pi }{\tau }}iz^{2}\right).}$

Then

${\displaystyle {\begin{aligned}\vartheta _{00}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{00}(z;\tau )\quad &\vartheta _{01}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{10}(z;\tau )\\[3pt]\vartheta _{10}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=\alpha \,\vartheta _{01}(z;\tau )\quad &\vartheta _{11}\!\left({\frac {z}{\tau }};{\frac {-1}{\tau }}\right)&=-i\alpha \,\vartheta _{11}(z;\tau ).\end{aligned}}}$

Instead of expressing the Theta functions in terms of z and τ, we may express them in terms of arguments w and the nome q, where w = e^πiz and q = e^πiτ. In this form, the functions become

${\displaystyle {\begin{aligned}\vartheta _{00}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n}q^{n^{2}}\quad &\vartheta _{01}(w,q)&=\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n}q^{n^{2}}\\[3pt]\vartheta _{10}(w,q)&=\sum _{n=-\infty }^{\infty }\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}\quad &\vartheta _{11}(w,q)&=i\sum _{n=-\infty }^{\infty }(-1)^{n}\left(w^{2}\right)^{n+{\frac {1}{2}}}q^{\left(n+{\frac {1}{2}}\right)^{2}}.\end{aligned}}}$

We see that the theta functions can also be defined in terms of w and q, without a direct reference to the exponential function. These formulas can, therefore, be used to define the Theta functions over other fields where the exponential function might not be everywhere defined, such as fields of p-adic numbers.

The Jacobi triple product (a special case of the Macdonald identities) tells us that for complex numbers w and q with |q| < 1 and w ≠ 0 we have

${\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+w^{2}q^{2m-1}\right)\left(1+w^{-2}q^{2m-1}\right)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

It can be proven by elementary means, as for instance in Hardy and Wright's An Introduction to the Theory of Numbers.

If we express the theta function in terms of the nome q = e^πiτ (noting some authors instead set q = e^2πiτ) and take w = e^πiz then

${\displaystyle \vartheta (z;\tau )=\sum _{n=-\infty }^{\infty }\exp(\pi i\tau n^{2})\exp(2\pi izn)=\sum _{n=-\infty }^{\infty }w^{2n}q^{n^{2}}.}$

We therefore obtain a product formula for the theta function in the form

${\displaystyle \vartheta (z;\tau )=\prod _{m=1}^{\infty }{\big (}1-\exp(2m\pi i\tau ){\big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau +2\pi iz{\big )}{\Big )}{\Big (}1+\exp {\big (}(2m-1)\pi i\tau -2\pi iz{\big )}{\Big )}.}$

In terms of w and q:

${\displaystyle {\begin{aligned}\vartheta (z;\tau )&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+q^{2m-1}w^{2}\right)\left(1+{\frac {q^{2m-1}}{w^{2}}}\right)\\&=\left(q^{2};q^{2}\right)_{\infty }\,\left(-w^{2}q;q^{2}\right)_{\infty }\,\left(-{\frac {q}{w^{2}}};q^{2}\right)_{\infty }\\&=\left(q^{2};q^{2}\right)_{\infty }\,\theta \left(-w^{2}q;q^{2}\right)\end{aligned}}}$

where (  ;  )_∞ is the q-Pochhammer symbol and θ(  ;  ) is the q-theta function. Expanding terms out, the Jacobi triple product can also be written

${\displaystyle \prod _{m=1}^{\infty }\left(1-q^{2m}\right){\Big (}1+\left(w^{2}+w^{-2}\right)q^{2m-1}+q^{4m-2}{\Big )},}$

which we may also write as

${\displaystyle \vartheta (z\mid q)=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right).}$

This form is valid in general but clearly is of particular interest when z is real. Similar product formulas for the auxiliary theta functions are

${\displaystyle {\begin{aligned}\vartheta _{01}(z\mid q)&=\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m-1}+q^{4m-2}\right),\\[3pt]\vartheta _{10}(z\mid q)&=2q^{\frac {1}{4}}\cos(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1+2\cos(2\pi z)q^{2m}+q^{4m}\right),\\[3pt]\vartheta _{11}(z\mid q)&=-2q^{\frac {1}{4}}\sin(\pi z)\prod _{m=1}^{\infty }\left(1-q^{2m}\right)\left(1-2\cos(2\pi z)q^{2m}+q^{4m}\right).\end{aligned}}}$

In particular, $${\displaystyle \lim _{q\to 0}{\frac {\vartheta _{10}(z\mid q)}{2q^{\frac {1}{4}}}}=\cos(\pi z),\quad \lim _{q\to 0}{\frac {-\vartheta _{11}(z\mid q)}{2q^{-{\frac {1}{4}}}}}=\sin(\pi z)}$$so we may interpret them as one-parameter deformations of the periodic functions ${\displaystyle \sin ,\cos }$, again validating the interpretation of the theta function as the most general 2 quasi-period function.

The Jacobi theta functions have the following integral representations:

${\displaystyle {\begin{aligned}\vartheta _{00}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{01}(z;\tau )&=-i\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{10}(z;\tau )&=-ie^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi u+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u;\\[6pt]\vartheta _{11}(z;\tau )&=e^{i\pi z+{\frac {1}{4}}i\pi \tau }\int _{i-\infty }^{i+\infty }e^{i\pi \tau u^{2}}{\frac {\cos(2\pi uz+\pi \tau u)}{\sin(\pi u)}}\mathrm {d} u.\end{aligned}}}$

The Theta Nullwert function ${\displaystyle \theta _{3}(q)}$ as this integral identity:

${\displaystyle \theta _{3}(q)=1+{\frac {4q{\sqrt {\ln(1/q)}}}{\sqrt {\pi }}}\int _{0}^{\infty }{\frac {\exp[-\ln(1/q)\,x^{2}]\{1-q^{2}\cos[2\ln(1/q)\,x]\}}{1-2q^{2}\cos[2\ln(1/q)\,x]+q^{4}}}\,\mathrm {d} x}$

This formula was discussed in the essay Square series generating function transformations by the mathematician Maxie Schmidt from Georgia in Atlanta.

Based on this formula following three eminent examples are given:

${\displaystyle {\biggl [}{\frac {2}{\pi }}K{\bigl (}{\frac {1}{2}}{\sqrt {2}}{\bigr )}{\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-\pi ){\bigr ]}=1+4\exp(-\pi )\int _{0}^{\infty }{\frac {\exp(-\pi x^{2})[1-\exp(-2\pi )\cos(2\pi x)]}{1-2\exp(-2\pi )\cos(2\pi x)+\exp(-4\pi )}}\,\mathrm {d} x}$

${\displaystyle {\biggl [}{\frac {2}{\pi }}K({\sqrt {2}}-1){\biggr ]}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {2}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{2}}\exp(-{\sqrt {2}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {2}}\,\pi x^{2})[1-\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)]}{1-2\exp(-2{\sqrt {2}}\,\pi )\cos(2{\sqrt {2}}\,\pi x)+\exp(-4{\sqrt {2}}\,\pi )}}\,\mathrm {d} x}$

${\displaystyle {\biggl \{}{\frac {2}{\pi }}K{\bigl [}\sin {\bigl (}{\frac {\pi }{12}}{\bigr )}{\bigr ]}{\biggr \}}^{1/2}=\theta _{3}{\bigl [}\exp(-{\sqrt {3}}\,\pi ){\bigr ]}=1+4\,{\sqrt[{4}]{3}}\exp(-{\sqrt {3}}\,\pi )\int _{0}^{\infty }{\frac {\exp(-{\sqrt {3}}\,\pi x^{2})[1-\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)]}{1-2\exp(-2{\sqrt {3}}\,\pi )\cos(2{\sqrt {3}}\,\pi x)+\exp(-4{\sqrt {3}}\,\pi )}}\,\mathrm {d} x}$

Furthermore, the theta examples ${\displaystyle \theta _{3}({\tfrac {1}{2}})}$ and ${\displaystyle \theta _{3}({\tfrac {1}{3}})}$ shall be displayed:

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{2^{n^{2}}}}=1+2\pi ^{-1/2}{\sqrt {\ln(2)}}\int _{0}^{\infty }{\frac {\exp[-\ln(2)\,x^{2}]\{16-4\cos[2\ln(2)\,x]\}}{17-8\cos[2\ln(2)\,x]}}\,\mathrm {d} x}$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{2}}{\bigr )}=2.128936827211877158669\ldots }$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1+2\sum _{n=1}^{\infty }{\frac {1}{3^{n^{2}}}}=1+{\frac {4}{3}}\pi ^{-1/2}{\sqrt {\ln(3)}}\int _{0}^{\infty }{\frac {\exp[-\ln(3)\,x^{2}]\{81-9\cos[2\ln(3)\,x]\}}{82-18\cos[2\ln(3)\,x]}}\,\mathrm {d} x}$

${\displaystyle \theta _{3}{\bigl (}{\frac {1}{3}}{\bigr )}=1.691459681681715341348\ldots }$

Proper credit for most of these results goes to Ramanujan. See Ramanujan's lost notebook and a relevant reference at Euler function. The Ramanujan results quoted at Euler function plus a few elementary operations give the results below, so they are either in Ramanujan's lost notebook or follow immediately from it. See also Yi (2004).^[4] Define,

${\displaystyle \quad \varphi (q)=\vartheta _{00}(0;\tau )=\theta _{3}(0;q)=\sum _{n=-\infty }^{\infty }q^{n^{2}}}$

with the nome ${\displaystyle q=e^{\pi i\tau },}$ ${\displaystyle \tau =n{\sqrt {-1}},}$ and Dedekind eta function ${\displaystyle \eta (\tau ).}$ Then for ${\displaystyle n=1,2,3,\dots }$

${\displaystyle {\begin{aligned}\varphi \left(e^{-\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}={\sqrt {2}}\,\eta \left({\sqrt {-1}}\right)\\\varphi \left(e^{-2\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {2+{\sqrt {2}}}}{2}}\\\varphi \left(e^{-3\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {1+{\sqrt {3}}}}{\sqrt[{8}]{108}}}\\\varphi \left(e^{-4\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {2+{\sqrt[{4}]{8}}}{4}}\\\varphi \left(e^{-5\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {2+{\sqrt {5}}}{5}}}\\\varphi \left(e^{-6\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}}}{\sqrt[{8}]{12^{3}}}}\\\varphi \left(e^{-7\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}}}{{\sqrt[{8}]{14^{3}}}\cdot {\sqrt[{16}]{7}}}}\\\varphi \left(e^{-8\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2+{\sqrt {2}}}}+{\sqrt[{8}]{128}}}{4}}\\\varphi \left(e^{-9\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {1+{\sqrt[{3}]{2+2{\sqrt {3}}}}}{3}}\\\varphi \left(e^{-10\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{64}}+{\sqrt[{4}]{80}}+{\sqrt[{4}]{81}}+{\sqrt[{4}]{100}}}}{\sqrt[{4}]{200}}}\\\varphi \left(e^{-11\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {11+{\sqrt {11}}+(5+3{\sqrt {3}}+{\sqrt {11}}+{\sqrt {33}}){\sqrt[{3}]{-44+33{\sqrt {3}}}}+(-5+3{\sqrt {3}}-{\sqrt {11}}+{\sqrt {33}}){\sqrt[{3}]{44+33{\sqrt {3}}}}}}{\sqrt[{8}]{52180524}}}\\\varphi \left(e^{-12\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt[{4}]{1}}+{\sqrt[{4}]{2}}+{\sqrt[{4}]{3}}+{\sqrt[{4}]{4}}+{\sqrt[{4}]{9}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{24}}}}{2{\sqrt[{8}]{108}}}}\\\varphi \left(e^{-13\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {13+8{\sqrt {13}}+(11-6{\sqrt {3}}+{\sqrt {13}}){\sqrt[{3}]{143+78{\sqrt {3}}}}+(11+6{\sqrt {3}}+{\sqrt {13}}){\sqrt[{3}]{143-78{\sqrt {3}}}}}}{\sqrt[{4}]{19773}}}\\\varphi \left(e^{-14\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {{\sqrt {13+{\sqrt {7}}}}+{\sqrt {7+3{\sqrt {7}}}}+{\sqrt {10+2{\sqrt {7}}}}+{\sqrt[{8}]{28}}{\sqrt {4+{\sqrt {7}}}}}}{\sqrt[{16}]{28^{7}}}}\\\varphi \left(e^{-15\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt {7+3{\sqrt {3}}+{\sqrt {5}}+{\sqrt {15}}+{\sqrt[{4}]{60}}+{\sqrt[{4}]{1500}}}}{{\sqrt[{8}]{12^{3}}}\cdot {\sqrt {5}}}}\\2\varphi \left(e^{-16\pi }\right)&=\varphi \left(e^{-4\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {\sqrt[{4}]{1+{\sqrt {2}}}}{\sqrt[{16}]{128}}}\\\varphi \left(e^{-17\pi }\right)&={\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\frac {{\sqrt {2}}(1+{\sqrt[{4}]{17}})+{\sqrt[{8}]{17}}{\sqrt {5+{\sqrt {17}}}}}{\sqrt {17+17{\sqrt {17}}}}}\\2\varphi \left(e^{-20\pi }\right)&=\varphi \left(e^{-5\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt {\frac {3+2{\sqrt[{4}]{5}}}{5{\sqrt {2}}}}}\\6\varphi \left(e^{-36\pi }\right)&=3\varphi \left(e^{-9\pi }\right)+2\varphi \left(e^{-4\pi }\right)-\varphi \left(e^{-\pi }\right)+{\frac {\sqrt[{4}]{\pi }}{\Gamma \left({\frac {3}{4}}\right)}}{\sqrt[{3}]{{\sqrt[{4}]{2}}+{\sqrt[{4}]{18}}+{\sqrt[{4}]{216}}}}\end{aligned}}}$

If the reciprocal of the Gelfond constant is raised to the power of the reciprocal of an odd number, then the corresponding ${\displaystyle \vartheta _{00}}$ values or ${\displaystyle \phi }$ values can be represented in a simplified way by using the hyperbolic lemniscatic sine:

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{5}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{5}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{5}}{\sqrt {2}}\,\varpi {\bigr )}}$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{7}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{7}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{7}}{\sqrt {2}}\,\varpi {\bigr )}}$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{9}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{9}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{9}}{\sqrt {2}}\,\varpi {\bigr )}}$

${\displaystyle \varphi {\bigl [}\exp(-{\tfrac {1}{11}}\pi ){\bigr ]}={\sqrt[{4}]{\pi }}\,{\Gamma \left({\tfrac {3}{4}}\right)}^{-1}\operatorname {slh} {\bigl (}{\tfrac {1}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {2}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {3}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {4}{11}}{\sqrt {2}}\,\varpi {\bigr )}\operatorname {slh} {\bigl (}{\tfrac {5}{11}}{\sqrt {2}}\,\varpi {\bigr )}}$

With the letter ${\displaystyle \varpi }$ the Lemniscate constant is represented.

Note that the following modular identities hold:

${\displaystyle {\begin{aligned}2\varphi \left(q^{4}\right)&=\varphi (q)+{\sqrt {2\varphi ^{2}\left(q^{2}\right)-\varphi ^{2}(q)}}\\3\varphi \left(q^{9}\right)&=\varphi (q)+{\sqrt[{3}]{9{\frac {\varphi ^{4}\left(q^{3}\right)}{\varphi (q)}}-\varphi ^{3}(q)}}\\{\sqrt {5}}\varphi \left(q^{25}\right)&=\varphi \left(q^{5}\right)\cot \left({\frac {1}{2}}\arctan \left({\frac {2}{\sqrt {5}}}{\frac {\varphi (q)\varphi \left(q^{5}\right)}{\varphi ^{2}(q)-\varphi ^{2}\left(q^{5}\right)}}{\frac {1+s(q)-s^{2}(q)}{s(q)}}\right)\right)\end{aligned}}}$

where ${\displaystyle s(q)=s\left(e^{\pi i\tau }\right)=-R\left(-e^{-\pi i/(5\tau )}\right)}$ is the Rogers–Ramanujan continued fraction:

${\displaystyle {\begin{aligned}s(q)&={\sqrt[{5}]{\tan \left({\frac {1}{2}}\arctan \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)\cot ^{2}\left({\frac {1}{2}}\operatorname {arccot} \left({\frac {5}{2}}{\frac {\varphi ^{2}\left(q^{5}\right)}{\varphi ^{2}(q)}}-{\frac {1}{2}}\right)\right)}}\\&={\cfrac {e^{-\pi i/(25\tau )}}{1-{\cfrac {e^{-\pi i/(5\tau )}}{1+{\cfrac {e^{-2\pi i/(5\tau )}}{1-\ddots }}}}}}\end{aligned}}}$

The mathematician Bruce Berndt found out further values^[5] of the theta function:

${\displaystyle {\begin{array}{lll}\varphi \left(\exp(-{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\\\varphi \left(\exp(-2{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{13/8}\cos({\tfrac {1}{24}}\pi )\\\varphi \left(\exp(-3{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{7/8}({\sqrt[{3}]{2}}+1)\\\varphi \left(\exp(-4{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-5/3}3^{13/8}{\Bigl (}1+{\sqrt {\cos({\tfrac {1}{12}}\pi )}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {3}}\,\pi )\right)&=&\pi ^{-1}{\Gamma \left({\tfrac {4}{3}}\right)}^{3/2}2^{-2/3}3^{5/8}\sin({\tfrac {1}{5}}\pi )({\tfrac {2}{5}}{\sqrt[{3}]{100}}+{\tfrac {2}{5}}{\sqrt[{3}]{10}}+{\tfrac {3}{5}}{\sqrt {5}}+1)\end{array}}}$

Many values of the theta function^[6] and especially of the shown phi function can be represented in terms of the gamma function:

${\displaystyle {\begin{array}{lll}\varphi \left(\exp(-{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{7/8}\\\varphi \left(\exp(-2{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{1/8}{\Bigl (}1+{\sqrt {{\sqrt {2}}-1}}{\Bigr )}\\\varphi \left(\exp(-3{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{3/8}3^{-1/2}({\sqrt {3}}+1){\sqrt {\tan({\tfrac {5}{24}}\pi )}}\\\varphi \left(\exp(-4{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}2^{-1/8}{\Bigl (}1+{\sqrt[{4}]{2{\sqrt {2}}-2}}{\Bigr )}\\\varphi \left(\exp(-5{\sqrt {2}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {9}{8}}\right){\Gamma \left({\tfrac {5}{4}}\right)}^{-1/2}{\frac {1}{15}}\,2^{3/8}\times \\&&\times {\biggl [}{\sqrt[{3}]{5}}\,{\sqrt {10+2{\sqrt {5}}}}{\biggl (}{\sqrt[{3}]{5+{\sqrt {2}}+3{\sqrt {3}}}}+{\sqrt[{3}]{5+{\sqrt {2}}-3{\sqrt {3}}}}\,{\biggr )}-{\bigl (}2-{\sqrt {2}}\,{\bigr )}{\sqrt {25-10{\sqrt {5}}}}\,{\biggr ]}\\\varphi \left(\exp(-{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{-13/24}3^{-1/8}{\sqrt {\sin({\tfrac {5}{12}}\pi )}}\\\varphi \left(\exp(-{\tfrac {1}{2}}{\sqrt {6}}\,\pi )\right)&=&\pi ^{-1/2}\Gamma \left({\tfrac {5}{24}}\right){\Gamma \left({\tfrac {5}{12}}\right)}^{-1/2}2^{5/24}3^{-1/8}\sin({\tfrac {5}{24}}\pi )\end{array}}}$

For the transformation of the nome^[7] in the theta functions these formulas can be used:

${\displaystyle \theta _{2}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}-\theta _{4}(q)^{2}]}}}$

${\displaystyle \theta _{3}(q^{2})={\tfrac {1}{2}}{\sqrt {2[\theta _{3}(q)^{2}+\theta _{4}(q)^{2}]}}}$

${\displaystyle \theta _{4}(q^{2})={\sqrt {\theta _{4}(q)\theta _{3}(q)}}}$

The squares of the three theta zero-value functions with the square function as the inner function are also formed in the pattern of the Pythagorean triples according to the Jacobi Identity. Furthermore, those transformations are valid:

${\displaystyle \theta _{3}(q^{4})={\tfrac {1}{2}}\theta _{3}(q)+{\tfrac {1}{2}}\theta _{4}(q)}$

These formulas can be used to compute the theta values of the cube of the nome:

${\displaystyle 27\,\theta _{3}(q^{3})^{8}-18\,\theta _{3}(q^{3})^{4}\theta _{3}(q)^{4}-\,\theta _{3}(q)^{8}=8\,\theta _{3}(q^{3})^{2}\theta _{3}(q)^{2}[2\,\theta _{4}(q)^{4}-\theta _{3}(q)^{4}]}$

${\displaystyle 27\,\theta _{4}(q^{3})^{8}-18\,\theta _{4}(q^{3})^{4}\theta _{4}(q)^{4}-\,\theta _{4}(q)^{8}=8\,\theta _{4}(q^{3})^{2}\theta _{4}(q)^{2}[2\,\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}$

And the following formulas can be used to compute the theta values of the fifth power of the nome:

${\displaystyle [\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}][5\,\theta _{3}(q^{5})^{2}-\theta _{3}(q)^{2}]^{5}=256\,\theta _{3}(q^{5})^{2}\theta _{3}(q)^{2}\theta _{4}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}$

${\displaystyle [\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}][5\,\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}]^{5}=256\,\theta _{4}(q^{5})^{2}\theta _{4}(q)^{2}\theta _{3}(q)^{4}[\theta _{3}(q)^{4}-\theta _{4}(q)^{4}]}$

The formulas for the theta Nullwert function values from the cube root of the elliptic nome are obtained by contrasting the two real solutions of the corresponding quartic equations:

${\displaystyle {\biggl [}{\frac {\theta _{3}(q^{1/3})^{2}}{\theta _{3}(q)^{2}}}-{\frac {3\,\theta _{3}(q^{3})^{2}}{\theta _{3}(q)^{2}}}{\biggr ]}^{2}=4-4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{4}(q)^{2}}{\theta _{3}(q)^{4}}}{\biggr ]}^{2/3}}$

${\displaystyle {\biggl [}{\frac {3\,\theta _{4}(q^{3})^{2}}{\theta _{4}(q)^{2}}}-{\frac {\theta _{4}(q^{1/3})^{2}}{\theta _{4}(q)^{2}}}{\biggr ]}^{2}=4+4{\biggl [}{\frac {2\,\theta _{2}(q)^{2}\theta _{3}(q)^{2}}{\theta _{4}(q)^{4}}}{\biggr ]}^{2/3}}$

The Rogers-Ramanujan continued fraction can be defined in terms of the Jacobi theta function in the following way:

${\displaystyle R(q)=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}}$

${\displaystyle R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{2/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {1}{2}}-{\frac {\theta _{4}(q)^{2}}{2\,\theta _{4}(q^{5})^{2}}}{\biggr ]}{\biggr \}}^{1/5}}$

${\displaystyle R(q^{2})=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}\tan {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}}$

The alternating Rogers-Ramanujan continued fraction function S(q) has the following two identities:

${\displaystyle S(q)={\frac {R(q^{4})}{R(q^{2})R(q)}}=\tan {\biggl \{}{\frac {1}{2}}\arctan {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{1/5}\cot {\biggl \{}{\frac {1}{2}}\operatorname {arccot} {\biggl [}{\frac {\theta _{3}(q)^{2}}{2\,\theta _{3}(q^{5})^{2}}}-{\frac {1}{2}}{\biggr ]}{\biggr \}}^{2/5}}$

The theta function values from the fifth root of the nome can be represented as a rational combination of the continued fractions R and S and the theta function values from the fifth power of the nome and the nome itself. The following four equations are valid for all values q between 0 and 1:

${\displaystyle {\frac {\theta _{3}(q^{1/5})}{\theta _{3}(q^{5})}}-1={\frac {1}{S(q)}}{\bigl [}S(q)^{2}+R(q^{2}){\bigr ]}{\bigl [}1+R(q^{2})S(q){\bigr ]}}$

${\displaystyle 1-{\frac {\theta _{4}(q^{1/5})}{\theta _{4}(q^{5})}}={\frac {1}{R(q)}}{\bigl [}R(q^{2})+R(q)^{2}{\bigr ]}{\bigl [}1-R(q^{2})R(q){\bigr ]}}$

${\displaystyle \theta _{3}(q^{1/5})^{2}-\theta _{3}(q)^{2}={\bigl [}\theta _{3}(q)^{2}-\theta _{3}(q^{5})^{2}{\bigr ]}{\biggl [}1+{\frac {1}{R(q^{2})S(q)}}+R(q^{2})S(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}+{\frac {1}{S(q)}}-S(q){\biggr ]}}$

${\displaystyle \theta _{4}(q)^{2}-\theta _{4}(q^{1/5})^{2}={\bigl [}\theta _{4}(q^{5})^{2}-\theta _{4}(q)^{2}{\bigr ]}{\biggl [}1-{\frac {1}{R(q^{2})R(q)}}-R(q^{2})R(q)+{\frac {1}{R(q^{2})^{2}}}+R(q^{2})^{2}-{\frac {1}{R(q)}}+R(q){\biggr ]}}$

Im combination with the elliptic modulus, following formulas can be displayed:

These are the formulas for the square of the elliptic nome:

${\displaystyle \theta _{4}[q(k)]=\theta _{4}[q(k)^{2}]{\sqrt[{8}]{1-k^{2}}}}$

${\displaystyle \theta _{4}[q(k)^{2}]=\theta _{3}[q(k)]{\sqrt[{8}]{1-k^{2}}}}$

${\displaystyle \theta _{3}[q(k)^{2}]=\theta _{3}[q(k)]\cos[{\tfrac {1}{2}}\arcsin(k)]}$

And this is an efficient formula for the cube of the nome: