Outerplanar graph

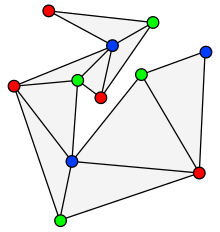
In graph theory, an outerplanar graph is a graph that has a planar drawing for which all vertices belong to the outer face of the drawing.

Outerplanar graphs may be characterized (analogously to Wagner's theorem for planar graphs) by the two forbidden minors K₄ and K_2,3, or by their Colin de Verdière graph invariants. They have Hamiltonian cycles if and only if they are biconnected, in which case the outer face forms the unique Hamiltonian cycle. Every outerplanar graph is 3-colorable, and has degeneracy and treewidth at most 2.

The outerplanar graphs are a subset of the planar graphs, the subgraphs of series–parallel graphs, and the circle graphs. The maximal outerplanar graphs, those to which no more edges can be added while preserving outerplanarity, are also chordal graphs and visibility graphs.

Outerplanar graphs were first studied and named by Chartrand & Harary (1967), in connection with the problem of determining the planarity of graphs formed by using a perfect matching to connect two copies of a base graph (for instance, many of the generalized Petersen graphs are formed in this way from two copies of a cycle graph). As they showed, when the base graph is biconnected, a graph constructed in this way is planar if and only if its base graph is outerplanar and the matching forms a dihedral permutation of its outer cycle. Chartrand and Harary also proved an analogue of Kuratowski's theorem for outerplanar graphs, that a graph is outerplanar if and only if it does not contain a subdivision of one of the two graphs K₄ or K_2,3.

An outerplanar graph is an undirected graph that can be drawn in the plane without crossings in such a way that all of the vertices belong to the unbounded face of the drawing. That is, no vertex is totally surrounded by edges. Alternatively, a graph G is outerplanar if the graph formed from G by adding a new vertex, with edges connecting it to all the other vertices, is a planar graph.^[1][2]

A maximal outerplanar graph is an outerplanar graph that cannot have any additional edges added to it while preserving outerplanarity. Every maximal outerplanar graph with n vertices has exactly 2n − 3 edges, and every bounded face of a maximal outerplanar graph is a triangle.

Outerplanar graphs have a forbidden graph characterization analogous to Kuratowski's theorem and Wagner's theorem for planar graphs: a graph is outerplanar if and only if it does not contain a subdivision of the complete graph K₄ or the complete bipartite graph K_2,3.^[3] Alternatively, a graph is outerplanar if and only if it does not contain K₄ or K_2,3 as a minor, a graph obtained from it by deleting and contracting edges.^[4]

A triangle-free graph is outerplanar if and only if it does not contain a subdivision of K_2,3.^[5]

A graph is outerplanar if and only if its Colin de Verdière graph invariant is at most two. The graphs characterized in a similar way by having Colin de Verdière invariant at most one, three, or four are respectively the linear forests, planar graphs, and linklessly embeddable graphs.

An outerplanar graph is biconnected if and only if the outer face of the graph forms a simple cycle without repeated vertices. An outerplanar graph is Hamiltonian if and only if it is biconnected; in this case, the outer face forms the unique Hamiltonian cycle.^[6] More generally, the size of the longest cycle in an outerplanar graph is the same as the number of vertices in its largest biconnected component. For this reason finding Hamiltonian cycles and longest cycles in outerplanar graphs may be solved in linear time, in contrast to the NP-completeness of these problems for arbitrary graphs.

Every maximal outerplanar graph satisfies a stronger condition than Hamiltonicity: it is node pancyclic, meaning that for every vertex v and every k in the range from three to the number of vertices in the graph, there is a length-k cycle containing v. A cycle of this length may be found by repeatedly removing a triangle that is connected to the rest of the graph by a single edge, such that the removed vertex is not v, until the outer face of the remaining graph has length k.^[7]

A planar graph is outerplanar if and only if each of its biconnected components is outerplanar.^[5]

All loopless outerplanar graphs can be colored using only three colors;^[8] this fact features prominently in the simplified proof of Chvátal's art gallery theorem by Fisk (1978). A 3-coloring may be found in linear time by a greedy coloring algorithm that removes any vertex of degree at most two, colors the remaining graph recursively, and then adds back the removed vertex with a color different from the colors of its two neighbors.

According to Vizing's theorem, the chromatic index of any graph (the minimum number of colors needed to color its edges so that no two adjacent edges have the same color) is either the maximum degree of any vertex of the graph or one plus the maximum degree. However, in a connected outerplanar graph, the chromatic index is equal to the maximum degree except when the graph forms a cycle of odd length.^[9] An edge coloring with an optimal number of colors can be found in linear time based on a breadth-first traversal of the weak dual tree.^[8]

Outerplanar graphs have degeneracy at most two: every subgraph of an outerplanar graph contains a vertex with degree at most two.^[10]

Outerplanar graphs have treewidth at most two, which implies that many graph optimization problems that are NP-complete for arbitrary graphs may be solved in polynomial time by dynamic programming when the input is outerplanar. More generally, k-outerplanar graphs have treewidth O(k).^[11]

Every outerplanar graph can be represented as an intersection graph of axis-aligned rectangles in the plane, so outerplanar graphs have boxicity at most two.^[12]

Every outerplanar graph is a planar graph. Every outerplanar graph is also a subgraph of a series–parallel graph.^[13] However, not all planar series–parallel graphs are outerplanar. The complete bipartite graph K_2,3 is planar and series–parallel but not outerplanar. On the other hand, the complete graph K₄ is planar but neither series–parallel nor outerplanar. Every forest and every cactus graph are outerplanar.^[14]

The weak planar dual graph of an embedded outerplanar graph (the graph that has a vertex for every bounded face of the embedding, and an edge for every pair of adjacent bounded faces) is a forest, and the weak planar dual of a Halin graph is an outerplanar graph. A planar graph is outerplanar if and only if its weak dual is a forest, and it is Halin if and only if its weak dual is biconnected and outerplanar.^[15]

There is a notion of degree of outerplanarity. A 1-outerplanar embedding of a graph is the same as an outerplanar embedding. For k > 1 a planar embedding is said to be k-outerplanar if removing the vertices on the outer face results in a (k − 1)-outerplanar embedding. A graph is k-outerplanar if it has a k-outerplanar embedding.^[16]

An outer-1-planar graph, analogously to 1-planar graphs can be drawn in a disk, with the vertices on the boundary of the disk, and with at most one crossing per edge.

Every maximal outerplanar graph is a chordal graph. Every maximal outerplanar graph is the visibility graph of a simple polygon.^[17] Maximal outerplanar graphs are also formed as the graphs of polygon triangulations. They are examples of 2-trees, of series–parallel graphs, and of chordal graphs.

Every outerplanar graph is a circle graph, the intersection graph of a set of chords of a circle.^[18]

• Outerplanar graphs at the Information System on Graph Classes and Their Inclusions
• Weisstein, Eric W. "Outplanar Graph". MathWorld.