Round-robin voting
| A joint Politics and Economics series |
| Social choice and electoral systems |
|---|
 |
| |
Round-robin, paired comparison, or tournament voting methods, are a set of ranked voting systems that choose winners by comparing every pair of candidates one-on-one, similar to a round-robin tournament.[1] In each paired matchup, we record the total number of voters who prefer each candidate in a beats matrix. Then, a majority-preferred (Condorcet) candidate is elected, if one exists. Otherwise, if there is a cyclic tie, the candidate "closest" to being a Condorcet winner is elected, based on the recorded beats matrix. How "closest" is defined varies by method.
Round-robin methods are one of the four major categories of single-winner electoral methods, along with multi-stage methods (like RCV-IRV), positional methods (like plurality and Borda), and graded methods (like score and STAR voting).
Most, but not all, election methods meeting the Condorcet criterion are based on pairwise counting.
Summary
[edit]In paired voting, each voter ranks candidates from first to last (or rates them on a scale).[2] For each pair of candidates (as in a round-robin tournament), we count how many votes rank each candidate over the other.[3]
Pairwise counting
[edit]Pairwise counts are often displayed in a pairwise comparison[4] or outranking matrix[5] such as those below. In these matrices, each row represents each candidate as a 'runner', while each column represents each candidate as an 'opponent'. The cells at the intersection of rows and columns each show the result of a particular pairwise comparison. Cells comparing a candidate to themselves are left blank.[6][7]
Imagine there is an election between four candidates: A, B, C and D. The first matrix below records the preferences expressed on a single ballot paper, in which the voter's preferences are B > C > A > D; that is, the voter ranked B first, C second, A third, and D fourth. In the matrix a '1' indicates that the runner is preferred over the opponent, while a '0' indicates that the opponent is preferred over the runner.[6][4]
Opponent Runner | A | B | C | D |
|---|---|---|---|---|
| A | — | 0 | 0 | 1 |
| B | 1 | — | 1 | 1 |
| C | 1 | 0 | — | 1 |
| D | 0 | 0 | 0 | — |
In this matrix the number in each cell indicates either the number of votes for runner over opponent (runner,opponent) or the number of votes for opponent over runner (opponent, runner).
If pairwise counting is used in an election that has three candidates named A, B, and C, the following pairwise counts are produced:
- A vs. B
- A vs. C
- B vs. C
If the number of voters who have no preference between two candidates is not supplied, it can be calculated using the supplied numbers. Specifically, start with the total number of voters in the election, then subtract the number of voters who prefer the first over the second, and then subtract the number of voters who prefer the second over the first.
The pairwise comparison matrix for these comparisons is shown below.[8]
| A | B | C | |
|---|---|---|---|
| A | A > B | A > C | |
| B | B > A | B > C | |
| C | C > A | C > B |
A candidate cannot be pairwise compared to itself (for example candidate A can't be compared to candidate A), so the cell that indicates this comparison is either empty or contains a 0.
Each ballot can be transformed into this style of matrix, and then added to all other ballot matrices using matrix addition. The resulting sum of all ballots in an election is called the sum matrix, and it summarizes all the voter preferences.
An election counting method can use the sum matrix to identify the winner of the election.
Suppose that this imaginary election has two additional voters, and their preferences are D > A > C > B and A > C > B > D. Added to the first voter, these ballots yield the following sum matrix:
Opponent Runner | A | B | C | D |
|---|---|---|---|---|
| A | — | 2 | 2 | 2 |
| B | 1 | — | 1 | 2 |
| C | 1 | 2 | — | 2 |
| D | 1 | 1 | 1 | — |
In the sum matrix above, A is the Condorcet winner, because they beats every other candidate one-on-one. When there is no Condorcet winner, ranked-robin methods such as ranked pairs use the information contained in the sum matrix to choose a winner.
The first matrix above, which represents a single ballot, is inversely symmetric: (runner,opponent) is ¬(opponent,runner). Or (runner,opponent) + (opponent,runner) = 1. The sum matrix has this property: (runner, opponent) + (opponent, runner) = N for N voters, if all runners are fully ranked by each voter.
Number of pairwise comparisons
[edit]For N candidates, there are N · (N − 1) pairwise matchups, assuming it is necessary to keep track of tied ranks. When working with margins, only half of these are necessary because storing both candidates' percentages becomes redundant.[9] For example, for 3 candidates there are 6 pairwise comparisons (and 3 pairwise margins), for 4 candidates there are 12 pairwise comparisons, and for 5 candidates there are 20 pairwise comparisons.
Example
[edit]
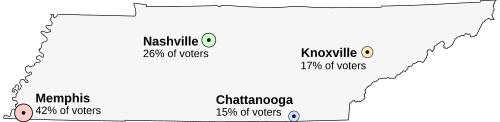
Suppose that Tennessee is holding an election on the location of its capital. The population is concentrated around four major cities. All voters want the capital to be as close to them as possible. The options are:
- Memphis, the largest city, but far from the others (42% of voters)
- Nashville, near the center of the state (26% of voters)
- Chattanooga, somewhat east (15% of voters)
- Knoxville, far to the northeast (17% of voters)
The preferences of each region's voters are:
| 42% of voters Far-West | 26% of voters Center | 15% of voters Center-East | 17% of voters Far-East |
|---|---|---|---|
|
|
|
|
These ranked preferences indicate which candidates the voter prefers. For example, the voters in the first column prefer Memphis as their 1st choice, Nashville as their 2nd choice, etc. As these ballot preferences are converted into pairwise counts they can be entered into a table.
The following square-grid table displays the candidates in the same order in which they appear above.
| ... over Memphis | ... over Nashville | ... over Chattanooga | ... over Knoxville | |
|---|---|---|---|---|
| Prefer Memphis ... | - | 42% | 42% | 42% |
| Prefer Nashville ... | 58% | - | 68% | 68% |
| Prefer Chattanooga ... | 58% | 32% | - | 83% |
| Prefer Knoxville ... | 58% | 32% | 17% | - |
The following tally table shows another table arrangement with the same numbers.[10]
| All possible pairs of candidates | Number of votes with indicated preference | Margin | |
|---|---|---|---|
| Prefer X to Y | Prefer Y to X | X − Y | |
| X = Memphis Y = Nashville | 42% | 58% | -16% |
| X = Memphis Y = Chattanooga | 42% | 58% | -16% |
| X = Memphis Y = Knoxville | 42% | 58% | -16% |
| X = Nashville Y = Chattanooga | 68% | 32% | +36% |
| X = Nashville Y = Knoxville | 68% | 32% | +36% |
| X = Chattanooga Y = Knoxville | 83% | 17% | +66% |
References
[edit]- ^ Foley, Edward B. (2021). "Tournament Elections with Round-Robin Primaries: A Sports Analogy for Electoral Reform". Wisconsin Law Review. 2021: 1187.
- ^ Darlington, Richard B. (2018). "Are Condorcet and minimax voting systems the best?". arXiv:1807.01366 [physics.soc-ph].
CC [Condorcet] systems typically allow tied ranks. If a voter fails to rank a candidate, they are typically presumed to rank them below anyone whom they did rank explicitly.
- ^ Hazewinkel, Michiel (2007-11-23). Encyclopaedia of Mathematics, Supplement III. Springer Science & Business Media. ISBN 978-0-306-48373-8.
Briefly, one can say candidate A defeats candidate B if a majority of the voters prefer A to B. With only two candidates [...] barring ties [...] one of the two candidates will defeat the other.
- ^ a b Mackie, Gerry. (2003). Democracy defended. Cambridge, UK: Cambridge University Press. p. 6. ISBN 0511062648. OCLC 252507400.
- ^ Nurmi, Hannu (2012), "On the Relevance of Theoretical Results to Voting System Choice", in Felsenthal, Dan S.; Machover, Moshé (eds.), Electoral Systems, Studies in Choice and Welfare, Springer Berlin Heidelberg, pp. 255–274, doi:10.1007/978-3-642-20441-8_10, ISBN 9783642204401, S2CID 12562825
- ^ a b Young, H. P. (1988). "Condorcet's Theory of Voting" (PDF). American Political Science Review. 82 (4): 1231–1244. doi:10.2307/1961757. ISSN 0003-0554. JSTOR 1961757.
- ^ Hogben, G. (1913). "Preferential Voting in Single-member Constituencies, with Special Reference to the Counting of Votes". Transactions and Proceedings of the Royal Society of New Zealand. 46: 304–308.
- ^ Mackie, Gerry (2003). Democracy Defended. Cambridge University Press. pp. 6–7. ISBN 0511062648.
- ^ Sloane, N. J. A. (ed.). "Sequence A000670 (Number of preferential arrangements of n labeled elements)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Fobes, Richard (2008). Crear soluciones:La Caja de Herramientas. p. 295. ISBN 978-9706662293.


 French
French Deutsch
Deutsch