French
DeutschPentagrammic prism
 | This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
| Uniform pentagrammic prism | |
|---|---|
 | |
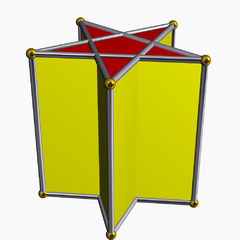| Type | Prismatic uniform polyhedron |
| Elements | F = 7, E = 15 V = 10 (χ = 2) |
| Faces by sides | 5{4}+2{5/2} |
| Schläfli symbol | t{2,5/2} or {5/2}×{} |
| Wythoff symbol | 2 5/2 | 2 |
| Coxeter diagram |       |
| Symmetry | D5h, [5,2], (*522), order 20 |
| Rotation group | D5, [5,2]+, (522), order 10 |
| Index references | U78(a) |
| Dual | Pentagrammic dipyramid |
| Properties | nonconvex |
 Vertex figure 4.4.5/2 | |
In geometry, the pentagrammic prism is one of an infinite set of nonconvex prisms formed by square sides and two regular star polygon caps, in this case two pentagrams.
It is a special case of a right prism with a pentagram as base, which in general has rectangular non-base faces. Topologically it is the same as a convex pentagonal prism.
It is the 78th model in the list of uniform polyhedra, as the first representative of uniform star prisms, along with the pentagrammic antiprism, which is the 79th model.
Geometry
[edit]It has 7 faces, 15 edges and 10 vertices. This polyhedron is identified with the indexed name U78 as a uniform polyhedron.[1]
The pentagram face has an ambiguous interior because it is self-intersecting. The central pentagon region can be considered interior or exterior, depending on how the interior is defined. One definition of the interior is the set of points from which a ray crosses the boundary an odd number of times; this makes the central pentagon exterior, as every ray beginning within it crosses two edges.
Gallery
[edit] An alternative representation with hollow centers to the pentagrams. |  3D model of a (uniform) pentagrammic prism |
Pentagrammic dipyramid
[edit]| Pentagrammic dipyramid | |
|---|---|
 | |
| Type | Star bipyramid |
| Faces | 10 triangles |
| Edges | 15 |
| Vertices | 7 |
| Schläfli symbol | {} + {5/2} |
| Coxeter diagram |   |
| Symmetry group | D5h, [5,2], (*225), order 20 |
| Rotation group | D5, [5,2]+, (225), order 10 |
| Dual polyhedron | pentagrammic prism |
| Face configuration | V4.4.5 |
| Properties | face-transitive, (deltahedron) |
In geometry, the pentagrammic dipyramid (or bipyramid) is first of the infinite set of face-transitive star dipyramids containing star polygon arrangement of edges. It has 10 intersecting isosceles triangle faces. It is topologically identical to the pentagonal dipyramid.
Each star dipyramid is the dual of a star polygon based uniform prism.
 3D model of a dual uniform pentagrammic dipyramid |  3D model of a pentagrammic dipyramid with regular faces |
Related polyhedra
[edit]There are two pentagrammic trapezohedra (or deltohedra), being dual to the pentagrammic antiprism and pentagrammic crossed antiprism respectively, each having intersecting kite-shaped faces (convex or concave), and a total of 12 vertices:
| {5⁄2} trapezohedron | {5⁄3} trapezohedron |
|---|---|
 |  |
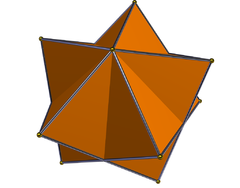References
[edit]- ^ Maeder, Roman. "78: pentagrammic prism". MathConsult.
External links
[edit]- Weisstein, Eric W. "Pentagrammic prism". MathWorld.
- Weisstein, Eric W. "Pentagrammic dipyramid". MathWorld.
- Weisstein, Eric W. "Pentagrammic deltohedron". MathWorld.
- Weisstein, Eric W. "Pentagrammic concave deltohedron". MathWorld.
- http://www.mathconsult.ch/showroom/unipoly/78.html
- http://bulatov.org/polyhedra/uniform/u03.html
- Paper model of pentagrammic prism
- https://web.archive.org/web/20050313234702/http://www.math.technion.ac.il/~rl/kaleido/data/03.html
- https://web.archive.org/web/20060211140715/http://www.ac-noumea.nc/maths/amc/polyhedr/no_conv5_.htm
- Paper Model (net) Pentagrammic Prism
 | This polyhedron-related article is a stub. You can help Wikipedia by expanding it. |