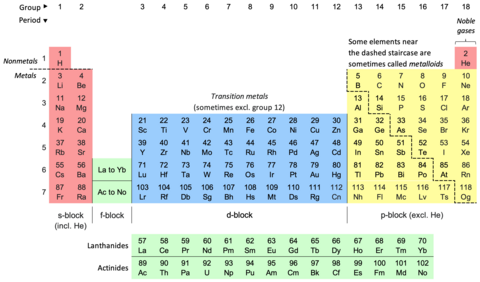
Periodic table
| Part of a series on the |
| Periodic table |
|---|
The periodic table, also known as the periodic table of the elements, is an ordered arrangement of the chemical elements into rows ("periods") and columns ("groups"). It is an icon of chemistry and is widely used in physics and other sciences. It is a depiction of the periodic law, which states that when the elements are arranged in order of their atomic numbers an approximate recurrence of their properties is evident. The table is divided into four roughly rectangular areas called blocks. Elements in the same group tend to show similar chemical characteristics.
Vertical, horizontal and diagonal trends characterize the periodic table. Metallic character increases going down a group and from right to left across a period. Nonmetallic character increases going from the bottom left of the periodic table to the top right.
The first periodic table to become generally accepted was that of the Russian chemist Dmitri Mendeleev in 1869; he formulated the periodic law as a dependence of chemical properties on atomic mass. As not all elements were then known, there were gaps in his periodic table, and Mendeleev successfully used the periodic law to predict some properties of some of the missing elements. The periodic law was recognized as a fundamental discovery in the late 19th century. It was explained early in the 20th century, with the discovery of atomic numbers and associated pioneering work in quantum mechanics, both ideas serving to illuminate the internal structure of the atom. A recognisably modern form of the table was reached in 1945 with Glenn T. Seaborg's discovery that the actinides were in fact f-block rather than d-block elements. The periodic table and law are now a central and indispensable part of modern chemistry.
The periodic table continues to evolve with the progress of science. In nature, only elements up to atomic number 94 exist;[a] to go further, it was necessary to synthesize new elements in the laboratory. By 2010, the first 118 elements were known, thereby completing the first seven rows of the table;[1] however, chemical characterization is still needed for the heaviest elements to confirm that their properties match their positions. New discoveries will extend the table beyond these seven rows, though it is not yet known how many more elements are possible; moreover, theoretical calculations suggest that this unknown region will not follow the patterns of the known part of the table. Some scientific discussion also continues regarding whether some elements are correctly positioned in today's table. Many alternative representations of the periodic law exist, and there is some discussion as to whether there is an optimal form of the periodic table.
Structure
| Group | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hydrogen & alkali metals | Alkaline earth metals | Triels | Tetrels | Pnictogens | Chalcogens | Halogens | Noble gases | ||||||||||||
| Period | |||||||||||||||||||
| 2 | |||||||||||||||||||
| 3 | |||||||||||||||||||
| 4 | |||||||||||||||||||
| 5 | |||||||||||||||||||
| 6 | |||||||||||||||||||
| 7 | |||||||||||||||||||
- Ca: 40.078 — Abridged value (uncertainty omitted here)[3]
- Po: [209] — mass number of the most stable isotope
Each chemical element has a unique atomic number (Z— for "Zahl", German for "number") representing the number of protons in its nucleus.[4] Each distinct atomic number therefore corresponds to a class of atom: these classes are called the chemical elements.[5] The chemical elements are what the periodic table classifies and organizes. Hydrogen is the element with atomic number 1; helium, atomic number 2; lithium, atomic number 3; and so on. Each of these names can be further abbreviated by a one- or two-letter chemical symbol; those for hydrogen, helium, and lithium are respectively H, He, and Li.[6] Neutrons do not affect the atom's chemical identity, but do affect its weight. Atoms with the same number of protons but different numbers of neutrons are called isotopes of the same chemical element.[6] Naturally occurring elements usually occur as mixes of different isotopes; since each isotope usually occurs with a characteristic abundance, naturally occurring elements have well-defined atomic weights, defined as the average mass of a naturally occurring atom of that element.[7] All elements have multiple isotopes, variants with the same number of protons but different numbers of neutrons. For example, carbon has three naturally occurring isotopes: all of its atoms have six protons and most have six neutrons as well, but about one per cent have seven neutrons, and a very small fraction have eight neutrons. Isotopes are never separated in the periodic table; they are always grouped together under a single element. When atomic mass is shown, it is usually the weighted average of naturally occurring isotopes; but if no isotopes occur naturally in significant quantities, the mass of the most stable isotope usually appears, often in parentheses.[8]
In the standard periodic table, the elements are listed in order of increasing atomic number. A new row (period) is started when a new electron shell has its first electron. Columns (groups) are determined by the electron configuration of the atom; elements with the same number of electrons in a particular subshell fall into the same columns (e.g. oxygen, sulfur, and selenium are in the same column because they all have four electrons in the outermost p-subshell). Elements with similar chemical properties generally fall into the same group in the periodic table, although in the f-block, and to some respect in the d-block, the elements in the same period tend to have similar properties, as well. Thus, it is relatively easy to predict the chemical properties of an element if one knows the properties of the elements around it.[9]
Today, 118 elements are known, the first 94 of which are known to occur naturally on Earth at present.[10][a] The remaining 24, americium to oganesson (95–118), occur only when synthesized in laboratories. Of the 94 naturally occurring elements, 83 are primordial and 11 occur only in decay chains of primordial elements. A few of the latter are so rare that they were not discovered in nature, but were synthesized in the laboratory before it was determined that they do exist in nature after all: technetium (element 43), promethium (element 61), astatine (element 85), neptunium (element 93), and plutonium (element 94).[12] No element heavier than einsteinium (element 99) has ever been observed in macroscopic quantities in its pure form, nor has astatine; francium (element 87) has been only photographed in the form of light emitted from microscopic quantities (300,000 atoms).[14] Of the 94 natural elements, eighty have a stable isotope and one more (bismuth) has an almost-stable isotope (with a half-life of 2.01×1019 years, over a billion times the age of the universe).[15][b] Two more, thorium and uranium, have isotopes undergoing radioactive decay with a half-life comparable to the age of the Earth. The stable elements plus bismuth, thorium, and uranium make up the 83 primordial elements that survived from the Earth's formation.[c] The remaining eleven natural elements decay quickly enough that their continued trace occurrence rests primarily on being constantly regenerated as intermediate products of the decay of thorium and uranium.[d] All 24 known artificial elements are radioactive.[6]
Group names and numbers
Under an international naming convention, the groups are numbered numerically from 1 to 18 from the leftmost column (the alkali metals) to the rightmost column (the noble gases). The f-block groups are ignored in this numbering.[22] Groups can also be named by their first element, e.g. the "scandium group" for group 3.[22] Previously, groups were known by Roman numerals. In the United States, the Roman numerals were followed by either an "A" if the group was in the s- or p-block, or a "B" if the group was in the d-block. The Roman numerals used correspond to the last digit of today's naming convention (e.g. the group 4 elements were group IVB, and the group 14 elements were group IVA). In Europe, the lettering was similar, except that "A" was used for groups 1 through 7, and "B" was used for groups 11 through 17. In addition, groups 8, 9 and 10 used to be treated as one triple-sized group, known collectively in both notations as group VIII. In 1988, the new IUPAC (International Union of Pure and Applied Chemistry) naming system (1–18) was put into use, and the old group names (I–VIII) were deprecated.[23]
| IUPAC group | 1a | 2 | —b | 3c | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mendeleev (I–VIII) | I | II | III | IV | V | VI | VII | VIII | I | II | III | IV | V | VI | VII | d | |||
| CAS (US, A-B-A) | IA | IIA | IIIB | IVB | VB | VIB | VIIB | VIIIB | IB | IIB | IIIA | IVA | VA | VIA | VIIA | VIIIA | |||
| Old IUPAC (Europe, A-B) | IA | IIA | IIIA | IVA | VA | VIA | VIIA | VIII | IB | IIB | IIIB | IVB | VB | VIB | VIIB | 0 | |||
| Trivial namer | H and alkali metals | alkaline earth metals | triels | tetrels | pnictogens | chalcogens | halogens | noble gases | |||||||||||
| Name by elementr | lithium group | beryllium group | scandium group | titanium group | vanadium group | chromium group | manganese group | iron group | cobalt group | nickel group | copper group | zinc group | boron group | carbon group | nitrogen group | oxygen group | fluorine group | helium or neon group | |
| Period 1 | H | He | |||||||||||||||||
| Period 2 | Li | Be | B | C | N | O | F | Ne | |||||||||||
| Period 3 | Na | Mg | Al | Si | P | S | Cl | Ar | |||||||||||
| Period 4 | K | Ca | Sc | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | Zn | Ga | Ge | As | Se | Br | Kr | |
| Period 5 | Rb | Sr | Y | Zr | Nb | Mo | Tc | Ru | Rh | Pd | Ag | Cd | In | Sn | Sb | Te | I | Xe | |
| Period 6 | Cs | Ba | La–Yb | Lu | Hf | Ta | W | Re | Os | Ir | Pt | Au | Hg | Tl | Pb | Bi | Po | At | Rn |
| Period 7 | Fr | Ra | Ac–No | Lr | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Nh | Fl | Mc | Lv | Ts | Og |
b The 14 f-block groups (columns) do not have a group number.
c The correct composition of group 3 is scandium (Sc), yttrium (Y), lutetium (Lu), and lawrencium (Lr), as shown here: this is endorsed by 1988[23] and 2021[24] IUPAC reports on the question. General inorganic chemistry texts often put scandium (Sc), yttrium (Y), lanthanum (La), and actinium (Ac) in group 3, so that Ce–Lu and Th–Lr become the f-block between groups 3 and 4; this was based on incorrectly measured electron configurations from history,[25] and Lev Landau and Evgeny Lifshitz already considered it incorrect in 1948.[26] Arguments can still occasionally be encountered in the contemporary literature purporting to defend it, but most authors consider them logically inconsistent.[27][28][29] Some sources follow a compromise that puts La–Lu and Ac–Lr as the f-block rows (despite that giving 15 f-block elements in each row, which contradicts quantum mechanics), leaving the heavier members of group 3 ambiguous.[24] See also Group 3 element#Composition.
d Group 18, the noble gases, were not discovered at the time of Mendeleev's original table. Later (1902), Mendeleev accepted the evidence for their existence, and they could be placed in a new "group 0", consistently and without breaking the periodic table principle.
r Group name as recommended by IUPAC.
Presentation forms
For reasons of space,[30][31] the periodic table is commonly presented with the f-block elements cut out and positioned as a distinct part below the main body.[32][30][23] This reduces the number of element columns from 32 to 18.[30]
Both forms represent the same periodic table.[6] The form with the f-block included in the main body is sometimes called the 32-column[6] or long form;[33] the form with the f-block cut out the 18-column[6] or medium-long form.[33] The 32-column form has the advantage of showing all elements in their correct sequence, but it has the disadvantage of requiring more space.[34] The form chosen is an editorial choice, and does not imply any change of scientific claim or statement. For example, when discussing the composition of group 3, the options can be shown equally (unprejudiced) in both forms.[35]
Periodic tables usually at least show the elements' symbols; many also provide supplementary information about the elements, either via colour-coding or as data in the cells. The above table shows the names and atomic numbers of the elements, and also their blocks, natural occurrences and standard atomic weights. For the short-lived elements without standard atomic weights, the mass number of the most stable known isotope is used instead. Other tables may include properties such as state of matter, melting and boiling points, densities, as well as provide different classifications of the elements.[e]
Electron configurations
The periodic table is a graphic description of the periodic law,[36] which states that the properties and atomic structures of the chemical elements are a periodic function of their atomic number.[37] Elements are placed in the periodic table according to their electron configurations,[38] the periodic recurrences of which explain the trends in properties across the periodic table.[39]
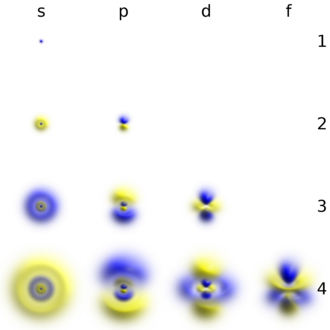
An electron can be thought of as inhabiting an atomic orbital, which characterizes the probability it can be found in any particular region around the atom. Their energies are quantised, which is to say that they can only take discrete values. Furthermore, electrons obey the Pauli exclusion principle: different electrons must always be in different states. This allows classification of the possible states an electron can take in various energy levels known as shells, divided into individual subshells, which each contain one or more orbitals. Each orbital can contain up to two electrons: they are distinguished by a quantity known as spin, conventionally labelled "up" or "down".[40][f] In a cold atom (one in its ground state), electrons arrange themselves in such a way that the total energy they have is minimized by occupying the lowest-energy orbitals available.[42] Only the outermost electrons (so-called valence electrons) have enough energy to break free of the nucleus and participate in chemical reactions with other atoms. The others are called core electrons.[43]
| ℓ = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | Shell capacity (2n2)[44] |
|---|---|---|---|---|---|---|---|---|
| Orbital | s | p | d | f | g | h | i | |
| n = 1 | 1s | 2 | ||||||
| n = 2 | 2s | 2p | 8 | |||||
| n = 3 | 3s | 3p | 3d | 18 | ||||
| n = 4 | 4s | 4p | 4d | 4f | 32 | |||
| n = 5 | 5s | 5p | 5d | 5f | 5g | 50 | ||
| n = 6 | 6s | 6p | 6d | 6f | 6g | 6h | 72 | |
| n = 7 | 7s | 7p | 7d | 7f | 7g | 7h | 7i | 98 |
| Subshell capacity (4ℓ+2) | 2 | 6 | 10 | 14 | 18 | 22 | 26 | |
Elements are known with up to the first seven shells occupied. The first shell contains only one orbital, a spherical s orbital. As it is in the first shell, this is called the 1s orbital. This can hold up to two electrons. The second shell similarly contains a 2s orbital, and it also contains three dumbbell-shaped 2p orbitals, and can thus fill up to eight electrons (2×1 + 2×3 = 8). The third shell contains one 3s orbital, three 3p orbitals, and five 3d orbitals, and thus has a capacity of 2×1 + 2×3 + 2×5 = 18. The fourth shell contains one 4s orbital, three 4p orbitals, five 4d orbitals, and seven 4f orbitals, thus leading to a capacity of 2×1 + 2×3 + 2×5 + 2×7 = 32.[30] Higher shells contain more types of orbitals that continue the pattern, but such types of orbitals are not filled in the ground states of known elements.[45] The subshell types are characterized by the quantum numbers. Four numbers describe an orbital in an atom completely: the principal quantum number n, the azimuthal quantum number ℓ (the orbital type), the orbital magnetic quantum number mℓ, and the spin magnetic quantum number ms.[39]
Order of subshell filling

The sequence in which the subshells are filled is given in most cases by the Aufbau principle, also known as the Madelung or Klechkovsky rule (after Erwin Madelung and Vsevolod Klechkovsky respectively). This rule was first observed empirically by Madelung, and Klechkovsky and later authors gave it theoretical justification.[46][47][48][49][g] The shells overlap in energies, and the Madelung rule specifies the sequence of filling according to:[47]
- 1s ≪ 2s < 2p ≪ 3s < 3p ≪ 4s < 3d < 4p ≪ 5s < 4d < 5p ≪ 6s < 4f < 5d < 6p ≪ 7s < 5f < 6d < 7p ≪ ...
Here the sign ≪ means "much less than" as opposed to < meaning just "less than".[47] Phrased differently, electrons enter orbitals in order of increasing n + ℓ, and if two orbitals are available with the same value of n + ℓ, the one with lower n is occupied first.[45][49] In general, orbitals with the same value of n + ℓ are similar in energy, but in the case of the s-orbitals (with ℓ = 0), quantum effects raise their energy to approach that of the next n + ℓ group. Hence the periodic table is usually drawn to begin each row (often called a period) with the filling of a new s-orbital, which corresponds to the beginning of a new shell.[47][48][30] Thus, with the exception of the first row, each period length appears twice:[47]
- 2, 8, 8, 18, 18, 32, 32, ...
The overlaps get quite close at the point where the d-orbitals enter the picture,[50] and the order can shift slightly with atomic number[51] and atomic charge.[52][h]
Starting from the simplest atom, this lets us build up the periodic table one at a time in order of atomic number, by considering the cases of single atoms. In hydrogen, there is only one electron, which must go in the lowest-energy orbital 1s. This electron configuration is written 1s1, where the superscript indicates the number of electrons in the subshell. Helium adds a second electron, which also goes into 1s, completely filling the first shell and giving the configuration 1s2.[39][58][i]
Starting from the third element, lithium, the first shell is full, so its third electron occupies a 2s orbital, giving a 1s2 2s1 configuration. The 2s electron is lithium's only valence electron, as the 1s subshell is now too tightly bound to the nucleus to participate in chemical bonding to other atoms: such a shell is called a "core shell". The 1s subshell is a core shell for all elements from lithium onward. The 2s subshell is completed by the next element beryllium (1s2 2s2). The following elements then proceed to fill the 2p subshell. Boron (1s2 2s2 2p1) puts its new electron in a 2p orbital; carbon (1s2 2s2 2p2) fills a second 2p orbital; and with nitrogen (1s2 2s2 2p3) all three 2p orbitals become singly occupied. This is consistent with Hund's rule, which states that atoms usually prefer to singly occupy each orbital of the same type before filling them with the second electron. Oxygen (1s2 2s2 2p4), fluorine (1s2 2s2 2p5), and neon (1s2 2s2 2p6) then complete the already singly filled 2p orbitals; the last of these fills the second shell completely.[39][58]
Starting from element 11, sodium, the second shell is full, making the second shell a core shell for this and all heavier elements. The eleventh electron begins the filling of the third shell by occupying a 3s orbital, giving a configuration of 1s2 2s2 2p6 3s1 for sodium. This configuration is abbreviated [Ne] 3s1, where [Ne] represents neon's configuration. Magnesium ([Ne] 3s2) finishes this 3s orbital, and the following six elements aluminium, silicon, phosphorus, sulfur, chlorine, and argon fill the three 3p orbitals ([Ne] 3s2 3p1 through [Ne] 3s2 3p6).[39][58] This creates an analogous series in which the outer shell structures of sodium through argon are analogous to those of lithium through neon, and is the basis for the periodicity of chemical properties that the periodic table illustrates:[39] at regular but changing intervals of atomic numbers, the properties of the chemical elements approximately repeat.[36]
The first eighteen elements can thus be arranged as the start of a periodic table. Elements in the same column have the same number of valence electrons and have analogous valence electron configurations: these columns are called groups. The single exception is helium, which has two valence electrons like beryllium and magnesium, but is typically placed in the column of neon and argon to emphasise that its outer shell is full. (Some contemporary authors question even this single exception, preferring to consistently follow the valence configurations and place helium over beryllium.) There are eight columns in this periodic table fragment, corresponding to at most eight outer-shell electrons.[32] A period begins when a new shell starts filling.[30] Finally, the colouring illustrates the blocks: the elements in the s-block (coloured red) are filling s-orbitals, while those in the p-block (coloured yellow) are filling p-orbitals.[30]
| 1 H | 2 He | 2×1 = 2 elements 1s | ||||||
| 3 Li | 4 Be | 5 B | 6 C | 7 N | 8 O | 9 F | 10 Ne | 2×(1+3) = 8 elements 2s 2p |
| 11 Na | 12 Mg | 13 Al | 14 Si | 15 P | 16 S | 17 Cl | 18 Ar | 2×(1+3) = 8 elements 3s 3p |
Starting the next row, for potassium and calcium the 4s subshell is the lowest in energy, and therefore they fill it.[39][58] Potassium adds one electron to the 4s shell ([Ar] 4s1), and calcium then completes it ([Ar] 4s2). However, starting from scandium ([Ar] 3d1 4s2) the 3d subshell becomes the next highest in energy. The 4s and 3d subshells have approximately the same energy and they compete for filling the electrons, and so the occupation is not quite consistently filling the 3d orbitals one at a time. The precise energy ordering of 3d and 4s changes along the row, and also changes depending on how many electrons are removed from the atom. For example, due to the repulsion between the 3d electrons and the 4s ones, at chromium the 4s energy level becomes slightly higher than 3d, and so it becomes more profitable for a chromium atom to have a [Ar] 3d5 4s1 configuration than an [Ar] 3d4 4s2 one. A similar anomaly occurs at copper, whose atom has a [Ar] 3d10 4s1 configuration rather than the expected [Ar] 3d9 4s2.[39] These are violations of the Madelung rule. Such anomalies, however, do not have any chemical significance:[52] most chemistry is not about isolated gaseous atoms,[60] and the various configurations are so close in energy to each other[50] that the presence of a nearby atom can shift the balance.[39] Therefore, the periodic table ignores them and considers only idealized configurations.[38]
At zinc ([Ar] 3d10 4s2), the 3d orbitals are completely filled with a total of ten electrons.[39][58] Next come the 4p orbitals, completing the row, which are filled progressively by gallium ([Ar] 3d10 4s2 4p1) through krypton ([Ar] 3d10 4s2 4p6), in a manner analogous to the previous p-block elements.[39][58] From gallium onwards, the 3d orbitals form part of the electronic core, and no longer participate in chemistry.[57] The s- and p-block elements, which fill their outer shells, are called main-group elements; the d-block elements (coloured blue below), which fill an inner shell, are called transition elements (or transition metals, since they are all metals).[61]
The next eighteen elements fill the 5s orbitals (rubidium and strontium), then 4d (yttrium through cadmium, again with a few anomalies along the way), and then 5p (indium through xenon).[30][58] Again, from indium onward the 4d orbitals are in the core.[58][62] Hence the fifth row has the same structure as the fourth.[30]
| 1 H | 2 He | 2×1 = 2 elements 1s | ||||||||||||||||
| 3 Li | 4 Be | 5 B | 6 C | 7 N | 8 O | 9 F | 10 Ne | 2×(1+3) = 8 elements 2s 2p | ||||||||||
| 11 Na | 12 Mg | 13 Al | 14 Si | 15 P | 16 S | 17 Cl | 18 Ar | 2×(1+3) = 8 elements 3s 3p | ||||||||||
| 19 K | 20 Ca | 21 Sc | 22 Ti | 23 V | 24 Cr | 25 Mn | 26 Fe | 27 Co | 28 Ni | 29 Cu | 30 Zn | 31 Ga | 32 Ge | 33 As | 34 Se | 35 Br | 36 Kr | 2×(1+3+5) = 18 elements 4s 3d 4p |
| 37 Rb | 38 Sr | 39 Y | 40 Zr | 41 Nb | 42 Mo | 43 Tc | 44 Ru | 45 Rh | 46 Pd | 47 Ag | 48 Cd | 49 In | 50 Sn | 51 Sb | 52 Te | 53 I | 54 Xe | 2×(1+3+5) = 18 elements 5s 4d 5p |
The sixth row of the table likewise starts with two s-block elements: caesium and barium.[58] After this, the first f-block elements (coloured green below) begin to appear, starting with lanthanum. These are sometimes termed inner transition elements.[61] As there are now not only 4f but also 5d and 6s subshells at similar energies, competition occurs once again with many irregular configurations;[50] this resulted in some dispute about where exactly the f-block is supposed to begin, but most who study the matter agree that it starts at lanthanum in accordance with the Aufbau principle.[27] Even though lanthanum does not itself fill the 4f subshell as a single atom, because of repulsion between electrons,[52] its 4f orbitals are low enough in energy to participate in chemistry.[63][53][64] At ytterbium, the seven 4f orbitals are completely filled with fourteen electrons; thereafter, a series of ten transition elements (lutetium through mercury) follows,[58][65][66][67] and finally six main-group elements (thallium through radon) complete the period.[58][68] From lutetium onwards the 4f orbitals are in the core,[58][64] and from thallium onwards so are the 5d orbitals.[58][57][69]
The seventh row is analogous to the sixth row: 7s fills (francium and radium), then 5f (actinium to nobelium), then 6d (lawrencium to copernicium), and finally 7p (nihonium to oganesson).[58] Starting from lawrencium the 5f orbitals are in the core,[58] and probably the 6d orbitals join the core starting from nihonium.[58][70][j] Again there are a few anomalies along the way:[30] for example, as single atoms neither actinium nor thorium actually fills the 5f subshell, and lawrencium does not fill the 6d shell, but all these subshells can still become filled in chemical environments.[72][73][74] For a very long time, the seventh row was incomplete as most of its elements do not occur in nature. The missing elements beyond uranium started to be synthesized in the laboratory in 1940, when neptunium was made.[75] (However, the first element to be discovered by synthesis rather than in nature was technetium in 1937.) The row was completed with the synthesis of tennessine in 2010[76] (the last element oganesson had already been made in 2002),[77] and the last elements in this seventh row were given names in 2016.[78]
| 1 H | 2 He | 2×1 = 2 elements 1s | ||||||||||||||||||||||||||||||
| 3 Li | 4 Be | 5 B | 6 C | 7 N | 8 O | 9 F | 10 Ne | 2×(1+3) = 8 elements 2s 2p | ||||||||||||||||||||||||
| 11 Na | 12 Mg | 13 Al | 14 Si | 15 P | 16 S | 17 Cl | 18 Ar | 2×(1+3) = 8 elements 3s 3p | ||||||||||||||||||||||||
| 19 K | 20 Ca | 21 Sc | 22 Ti | 23 V | 24 Cr | 25 Mn | 26 Fe | 27 Co | 28 Ni | 29 Cu | 30 Zn | 31 Ga | 32 Ge | 33 As | 34 Se | 35 Br | 36 Kr | 2×(1+3+5) = 18 elements 4s 3d 4p | ||||||||||||||
| 37 Rb | 38 Sr | 39 Y | 40 Zr | 41 Nb | 42 Mo | 43 Tc | 44 Ru | 45 Rh | 46 Pd | 47 Ag | 48 Cd | 49 In | 50 Sn | 51 Sb | 52 Te | 53 I | 54 Xe | 2×(1+3+5) = 18 elements 5s 4d 5p | ||||||||||||||
| 55 Cs | 56 Ba | 57 La | 58 Ce | 59 Pr | 60 Nd | 61 Pm | 62 Sm | 63 Eu | 64 Gd | 65 Tb | 66 Dy | 67 Ho | 68 Er | 69 Tm | 70 Yb | 71 Lu | 72 Hf | 73 Ta | 74 W | 75 Re | 76 Os | 77 Ir | 78 Pt | 79 Au | 80 Hg | 81 Tl | 82 Pb | 83 Bi | 84 Po | 85 At | 86 Rn | 2×(1+3+5+7) = 32 elements 6s 4f 5d 6p |
| 87 Fr | 88 Ra | 89 Ac | 90 Th | 91 Pa | 92 U | 93 Np | 94 Pu | 95 Am | 96 Cm | 97 Bk | 98 Cf | 99 Es | 100 Fm | 101 Md | 102 No | 103 Lr | 104 Rf | 105 Db | 106 Sg | 107 Bh | 108 Hs | 109 Mt | 110 Ds | 111 Rg | 112 Cn | 113 Nh | 114 Fl | 115 Mc | 116 Lv | 117 Ts | 118 Og | 2×(1+3+5+7) = 32 elements 7s 5f 6d 7p |
This completes the modern periodic table, with all seven rows completely filled to capacity.[78]
Electron configuration table
The following table shows the electron configuration of a neutral gas-phase atom of each element. Different configurations can be favoured in different chemical environments.[52] The main-group elements have entirely regular electron configurations; the transition and inner transition elements show twenty irregularities due to the aforementioned competition between subshells close in energy level. For the last ten elements (109–118), experimental data is lacking[79] and therefore calculated configurations have been shown instead.[80] Completely filled subshells have been greyed out.
| Group: | 1 | 2 | | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1s: | 1 H 1 | 2 He 2 | ||||||||||||||||||||||||||||||
| [He] 2s: 2p: | 3 Li 1 - | 4 Be 2 - | 5 B 2 1 | 6 C 2 2 | 7 N 2 3 | 8 O 2 4 | 9 F 2 5 | 10 Ne 2 6 | ||||||||||||||||||||||||
| [Ne] 3s: 3p: | 11 Na 1 - | 12 Mg 2 - | 13 Al 2 1 | 14 Si 2 2 | 15 P 2 3 | 16 S 2 4 | 17 Cl 2 5 | 18 Ar 2 6 | ||||||||||||||||||||||||
| [Ar] 4s: 3d: 4p: | 19 K 1 - - | 20 Ca 2 - - | 21 Sc 2 1 - | 22 Ti 2 2 - | 23 V 2 3 - | 24 Cr 1 5 - | 25 Mn 2 5 - | 26 Fe 2 6 - | 27 Co 2 7 - | 28 Ni 2 8 - | 29 Cu 1 10 - | 30 Zn 2 10 - | 31 Ga 2 10 1 | 32 Ge 2 10 2 | 33 As 2 10 3 | 34 Se 2 10 4 | 35 Br 2 10 5 | 36 Kr 2 10 6 | ||||||||||||||
| [Kr] 5s: 4d: 5p: | 37 Rb 1 - - | 38 Sr 2 - - | 39 Y 2 1 - | 40 Zr 2 2 - | 41 Nb 1 4 - | 42 Mo 1 5 - | 43 Tc 2 5 - | 44 Ru 1 7 - | 45 Rh 1 8 - | 46 Pd - 10 - | 47 Ag 1 10 - | 48 Cd 2 10 - | 49 In 2 10 1 | 50 Sn 2 10 2 | 51 Sb 2 10 3 | 52 Te 2 10 4 | 53 I 2 10 5 | 54 Xe 2 10 6 | ||||||||||||||
| [Xe] 6s: 4f: 5d: 6p: | 55 Cs 1 - - - | 56 Ba 2 - - - | 57 La 2 - 1 - | 58 Ce 2 1 1 - | 59 Pr 2 3 - - | 60 Nd 2 4 - - | 61 Pm 2 5 - - | 62 Sm 2 6 - - | 63 Eu 2 7 - - | 64 Gd 2 7 1 - | 65 Tb 2 9 - - | 66 Dy 2 10 - - | 67 Ho 2 11 - - | 68 Er 2 12 - - | 69 Tm 2 13 - - | 70 Yb 2 14 - - | 71 Lu 2 14 1 - | 72 Hf 2 14 2 - | 73 Ta 2 14 3 - | 74 W 2 14 4 - | 75 Re 2 14 5 - | 76 Os 2 14 6 - | 77 Ir 2 14 7 - | 78 Pt 1 14 9 - | 79 Au 1 14 10 - | 80 Hg 2 14 10 - | 81 Tl 2 14 10 1 | 82 Pb 2 14 10 2 | 83 Bi 2 14 10 3 | 84 Po 2 14 10 4 | 85 At 2 14 10 5 | 86 Rn 2 14 10 6 |
| [Rn] 7s: 5f: 6d: 7p: | 87 Fr 1 - - - | 88 Ra 2 - - - | 89 Ac 2 - 1 - | 90 Th 2 - 2 - | 91 Pa 2 2 1 - | 92 U 2 3 1 - | 93 Np 2 4 1 - | 94 Pu 2 6 - - | 95 Am 2 7 - - | 96 Cm 2 7 1 - | 97 Bk 2 9 - - | 98 Cf 2 10 - - | 99 Es 2 11 - - | 100 Fm 2 12 - - | 101 Md 2 13 - - | 102 No 2 14 - - | 103 Lr 2 14 - 1 | 104 Rf 2 14 2 - | 105 Db 2 14 3 - | 106 Sg 2 14 4 - | 107 Bh 2 14 5 - | 108 Hs 2 14 6 - | 109 Mt 2 14 7 - | 110 Ds 2 14 8 - | 111 Rg 2 14 9 - | 112 Cn 2 14 10 - | 113 Nh 2 14 10 1 | 114 Fl 2 14 10 2 | 115 Mc 2 14 10 3 | 116 Lv 2 14 10 4 | 117 Ts 2 14 10 5 | 118 Og 2 14 10 6 |
| | ||||||||||||||||||||||||||||||||
Variations
Period 1
Although the modern periodic table is standard today, the placement of the period 1 elements hydrogen and helium remains an open issue under discussion, and some variation can be found.[57][81] Following their respective s1 and s2 electron configurations, hydrogen would be placed in group 1, and helium would be placed in group 2.[57] The group 1 placement of hydrogen is common, but helium is almost always placed in group 18 with the other noble gases.[6] The debate has to do with conflicting understandings of the extent to which chemical or electronic properties should decide periodic table placement.[81]
Like the group 1 metals, hydrogen has one electron in its outermost shell[82] and typically loses its only electron in chemical reactions.[83] Hydrogen has some metal-like chemical properties, being able to displace some metals from their salts.[83] But it forms a diatomic nonmetallic gas at standard conditions, unlike the alkali metals which are reactive solid metals. This and hydrogen's formation of hydrides, in which it gains an electron, brings it close to the properties of the halogens which do the same[83] (though it is rarer for hydrogen to form H− than H+).[84] Moreover, the lightest two halogens (fluorine and chlorine) are gaseous like hydrogen at standard conditions.[83] Some properties of hydrogen are not a good fit for either group: hydrogen is neither highly oxidizing nor highly reducing and is not reactive with water.[84] Hydrogen thus has properties corresponding to both those of the alkali metals and the halogens, but matches neither group perfectly, and is thus difficult to place by its chemistry.[83] Therefore, while the electronic placement of hydrogen in group 1 predominates, some rarer arrangements show either hydrogen in group 17,[85] duplicate hydrogen in both groups 1 and 17,[86][87] or float it separately from all groups.[87][88][57] This last option has nonetheless been criticized by the chemist and philosopher of science Eric Scerri on the grounds that it appears to imply that hydrogen is above the periodic law altogether, unlike all the other elements.[89]
Helium is the only element that routinely occupies a position in the periodic table that is not consistent with its electronic structure. It has two electrons in its outermost shell, whereas the other noble gases have eight; and it is an s-block element, whereas all other noble gases are p-block elements. However it is unreactive at standard conditions, and has a full outer shell: these properties are like the noble gases in group 18, but not at all like the reactive alkaline earth metals of group 2. For these reasons helium is nearly universally placed in group 18[6] which its properties best match;[57] a proposal to move helium to group 2 was rejected by IUPAC in 1988 for these reasons.[23] Nonetheless, helium is still occasionally placed in group 2 today,[90] and some of its physical and chemical properties are closer to the group 2 elements and support the electronic placement.[82][57] Solid helium crystallises in a hexagonal close-packed structure, which matches beryllium and magnesium in group 2, but not the other noble gases in group 18.[91] Recent theoretical developments in noble gas chemistry, in which helium is expected to show slightly less inertness than neon and to form (HeO)(LiF)2 with a structure similar to the analogous beryllium compound (but with no expected neon analogue), have resulted in more chemists advocating a placement of helium in group 2. This relates to the electronic argument, as the reason for neon's greater inertness is repulsion from its filled p-shell that helium lacks, though realistically it is unlikely that helium-containing molecules will be stable outside extreme low-temperature conditions (around 10 K).[92][93][94][95]
The first-row anomaly in the periodic table has additionally been cited to support moving helium to group 2. It arises because the first orbital of any type is unusually small, since unlike its higher analogues, it does not experience interelectronic repulsion from a smaller orbital of the same type. This makes the first row of elements in each block unusually small, and such elements tend to exhibit characteristic kinds of anomalies for their group. Some chemists arguing for the repositioning of helium have pointed out that helium exhibits these anomalies if it is placed in group 2, but not if it is placed in group 18: on the other hand, neon, which would be the first group 18 element if helium was removed from that spot, does exhibit those anomalies.[92] The relationship between helium and beryllium is then argued to resemble that between hydrogen and lithium, a placement which is much more commonly accepted.[93] For example, because of this trend in the sizes of orbitals, a large difference in atomic radii between the first and second members of each main group is seen in groups 1 and 13–17: it exists between neon and argon, and between helium and beryllium, but not between helium and neon. This similarly affects the noble gases' boiling points and solubilities in water, where helium is too close to neon, and the large difference characteristic between the first two elements of a group appears only between neon and argon. Moving helium to group 2 makes this trend consistent in groups 2 and 18 as well, by making helium the first group 2 element and neon the first group 18 element: both exhibit the characteristic properties of a kainosymmetric first element of a group.[96][97] The group 18 placement of helium nonetheless remains near-universal due to its extreme inertness.[98] Additionally, tables that float both hydrogen and helium outside all groups may rarely be encountered.[88][57][58]
Group 3
In many periodic tables, the f-block is shifted one element to the right, so that lanthanum and actinium become d-block elements in group 3, and Ce–Lu and Th–Lr form the f-block. Thus the d-block is split into two very uneven portions. This is a holdover from early mistaken measurements of electron configurations; modern measurements are more consistent with the form with lutetium and lawrencium in group 3, and with La–Yb and Ac–No as the f-block.[25][99]
The 4f shell is completely filled at ytterbium, and for that reason Lev Landau and Evgeny Lifshitz in 1948 considered it incorrect to group lutetium as an f-block element.[26] They did not yet take the step of removing lanthanum from the d-block as well, but Jun Kondō realized in 1963 that lanthanum's low-temperature superconductivity implied the activity of its 4f shell.[100] In 1965, David C. Hamilton linked this observation to its position in the periodic table, and argued that the f-block should be composed of the elements La–Yb and Ac–No.[63] Since then, physical, chemical, and electronic evidence has supported this assignment.[25][23][99] The issue was brought to wide attention by William B. Jensen in 1982,[25] and the reassignment of lutetium and lawrencium to group 3 was supported by IUPAC reports dating from 1988 (when the 1–18 group numbers were recommended)[23] and 2021.[24] The variation nonetheless still exists because most textbook writers are not aware of the issue.[25]
A third form can sometimes be encountered in which the spaces below yttrium in group 3 are left empty, such as the table appearing on the IUPAC web site,[6] but this creates an inconsistency with quantum mechanics by making the f-block 15 elements wide (La–Lu and Ac–Lr) even though only 14 electrons can fit in an f-subshell.[24] There is moreover some confusion in the literature on which elements are then implied to be in group 3.[24][33][101][102][103] While the 2021 IUPAC report noted that 15-element-wide f-blocks are supported by some practitioners of a specialized branch of relativistic quantum mechanics focusing on the properties of superheavy elements, the project's opinion was that such interest-dependent concerns should not have any bearing on how the periodic table is presented to "the general chemical and scientific community".[24] Other authors focusing on superheavy elements since clarified that the "15th entry of the f-block represents the first slot of the d-block which is left vacant to indicate the place of the f-block inserts", which would imply that this form still has lutetium and lawrencium (the 15th entries in question) as d-block elements in group 3.[104] Indeed, when IUPAC publications expand the table to 32 columns, they make this clear and place lutetium and lawrencium under yttrium in group 3.[105][106]
Several arguments in favour of Sc-Y-La-Ac can be encountered in the literature,[107][108] but they have been challenged as being logically inconsistent.[27][28][29] For example, it has been argued that lanthanum and actinium cannot be f-block elements because as individual gas-phase atoms, they have not begun to fill the f-subshells.[109] But the same is true of thorium which is never disputed as an f-block element,[24][25] and this argument overlooks the problem on the other end: that the f-shells complete filling at ytterbium and nobelium, matching the Sc-Y-Lu-Lr form, and not at lutetium and lawrencium as the Sc-Y-La-Ac form would have it.[110] Not only are such exceptional configurations in the minority,[110] but they have also in any case never been considered as relevant for positioning any other elements on the periodic table: in gaseous atoms, the d-shells complete their filling at copper, palladium, and gold, but it is universally accepted by chemists that these configurations are exceptional and that the d-block really ends in accordance with the Madelung rule at zinc, cadmium, and mercury.[33] The relevant fact for placement[38][65] is that lanthanum and actinium (like thorium) have valence f-orbitals that can become occupied in chemical environments, whereas lutetium and lawrencium do not:[58][111][74] their f-shells are in the core, and cannot be used for chemical reactions.[64][112] Thus the relationship between yttrium and lanthanum is only a secondary relationship between elements with the same number of valence electrons but different kinds of valence orbitals, such as that between chromium and uranium; whereas the relationship between yttrium and lutetium is primary, sharing both valence electron count and valence orbital type.[58]
Periodic trends
As chemical reactions involve the valence electrons,[32] elements with similar outer electron configurations may be expected to react similarly and form compounds with similar proportions of elements in them.[113] Such elements are placed in the same group, and thus there tend to be clear similarities and trends in chemical behaviour as one proceeds down a group.[114] As analogous configurations occur at regular intervals, the properties of the elements thus exhibit periodic recurrences, hence the name of the periodic table and the periodic law. These periodic recurrences were noticed well before the underlying theory that explains them was developed.[115][116]
Atomic radius
Historically, the physical size of atoms was unknown until the early 20th century. The first calculated estimate of the atomic radius of hydrogen was published by physicist Arthur Haas in 1910 to within an order of magnitude (a factor of 10) of the accepted value, the Bohr radius (~0.529 Å). In his model, Haas used a single-electron configuration based on the classical atomic model proposed by J. J. Thomson in 1904, often called the plum-pudding model.[117]
Atomic radii (the size of atoms) are dependent on the sizes of their outermost orbitals.[96] They generally decrease going left to right along the main-group elements, because the nuclear charge increases but the outer electrons are still in the same shell. However, going down a column, the radii generally increase, because the outermost electrons are in higher shells that are thus further away from the nucleus.[32][118] The first row of each block is abnormally small, due to an effect called kainosymmetry or primogenic repulsion:[119] the 1s, 2p, 3d, and 4f subshells have no inner analogues. For example, the 2p orbitals do not experience strong repulsion from the 1s and 2s orbitals, which have quite different angular charge distributions, and hence are not very large; but the 3p orbitals experience strong repulsion from the 2p orbitals, which have similar angular charge distributions. Thus higher s-, p-, d-, and f-subshells experience strong repulsion from their inner analogues, which have approximately the same angular distribution of charge, and must expand to avoid this. This makes significant differences arise between the small 2p elements, which prefer multiple bonding, and the larger 3p and higher p-elements, which do not.[96] Similar anomalies arise for the 1s, 2p, 3d, 4f, and the hypothetical 5g elements:[120] the degree of this first-row anomaly is highest for the s-block, is moderate for the p-block, and is less pronounced for the d- and f-blocks.[121]
In the transition elements, an inner shell is filling, but the size of the atom is still determined by the outer electrons. The increasing nuclear charge across the series and the increased number of inner electrons for shielding somewhat compensate each other, so the decrease in radius is smaller.[118] The 4p and 5d atoms, coming immediately after new types of transition series are first introduced, are smaller than would have been expected,[122] because the added core 3d and 4f subshells provide only incomplete shielding of the nuclear charge for the outer electrons. Hence for example gallium atoms are slightly smaller than aluminium atoms.[96] Together with kainosymmetry, this results in an even-odd difference between the periods (except in the s-block)[k] that is sometimes known as secondary periodicity: elements in even periods have smaller atomic radii and prefer to lose fewer electrons, while elements in odd periods (except the first) differ in the opposite direction. Thus for example many properties in the p-block show a zigzag rather than a smooth trend along the group. For example, phosphorus and antimony in odd periods of group 15 readily reach the +5 oxidation state, whereas nitrogen, arsenic, and bismuth in even periods prefer to stay at +3.[121][123] A similar situation holds for the d-block, with lutetium through tungsten atoms being slightly smaller than yttrium through molybdenum atoms respectively.[124][125]

Thallium and lead atoms are about the same size as indium and tin atoms respectively, but from bismuth to radon the 6p atoms are larger than the analogous 5p atoms. This happens because when atomic nuclei become highly charged, special relativity becomes needed to gauge the effect of the nucleus on the electron cloud. These relativistic effects result in heavy elements increasingly having differing properties compared to their lighter homologues in the periodic table. Spin–orbit interaction splits the p-subshell: one p-orbital is relativistically stabilized and shrunken (it fills in thallium and lead), but the other two (filling in bismuth through radon) are relativistically destabilized and expanded.[96] Relativistic effects also explain why gold is golden and mercury is a liquid at room temperature.[126][127] They are expected to become very strong in the late seventh period, potentially leading to a collapse of periodicity.[128] Electron configurations are only clearly known until element 108 (hassium), and experimental chemistry beyond 108 has only been done for 112 (copernicium), 113 (nihonium), and 114 (flerovium), so the chemical characterization of the heaviest elements remains a topic of current research.[129]
The trend that atomic radii decrease from left to right is also present in ionic radii, though it is more difficult to examine because the most common ions of consecutive elements normally differ in charge. Ions with the same electron configuration decrease in size as their atomic number rises, due to increased attraction from the more positively charged nucleus: thus for example ionic radii decrease in the series Se2−, Br−, Rb+, Sr2+, Y3+, Zr4+, Nb5+, Mo6+, Tc7+. Ions of the same element get smaller as more electrons are removed, because the attraction from the nucleus begins to outweigh the repulsion between electrons that causes electron clouds to expand: thus for example ionic radii decrease in the series V2+, V3+, V4+, V5+.[130]
Ionisation energy

The first ionisation energy of an atom is the energy required to remove an electron from it. This varies with the atomic radius: ionisation energy increases left to right and down to up, because electrons that are closer to the nucleus are held more tightly and are more difficult to remove. Ionisation energy thus is minimized at the first element of each period – hydrogen and the alkali metals – and then generally rises until it reaches the noble gas at the right edge of the period.[32] There are some exceptions to this trend, such as oxygen, where the electron being removed is paired and thus interelectronic repulsion makes it easier to remove than expected.[131]
In the transition series, the outer electrons are preferentially lost even though the inner orbitals are filling. For example, in the 3d series, the 4s electrons are lost first even though the 3d orbitals are being filled. The shielding effect of adding an extra 3d electron approximately compensates the rise in nuclear charge, and therefore the ionisation energies stay mostly constant, though there is a small increase especially at the end of each transition series.[132]
As metal atoms tend to lose electrons in chemical reactions, ionisation energy is generally correlated with chemical reactivity, although there are other factors involved as well.[132]
Electron affinity
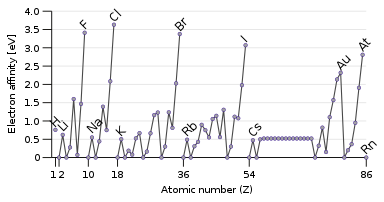
The opposite property to ionisation energy is the electron affinity, which is the energy released when adding an electron to the atom.[133] A passing electron will be more readily attracted to an atom if it feels the pull of the nucleus more strongly, and especially if there is an available partially filled outer orbital that can accommodate it. Therefore, electron affinity tends to increase down to up and left to right. The exception is the last column, the noble gases, which have a full shell and have no room for another electron. This gives the halogens in the next-to-last column the highest electron affinities.[32]
Some atoms, like the noble gases, have no electron affinity: they cannot form stable gas-phase anions.[134] (They can form metastable resonances if the incoming electron arrives with enough kinetic energy, but these inevitably and rapidly autodetach: for example, the lifetime of the most long-lived He− level is about 359 microseconds.)[135] The noble gases, having high ionisation energies and no electron affinity, have little inclination towards gaining or losing electrons and are generally unreactive.[32]
Some exceptions to the trends occur: oxygen and fluorine have lower electron affinities than their heavier homologues sulfur and chlorine, because they are small atoms and hence the newly added electron would experience significant repulsion from the already present ones. For the nonmetallic elements, electron affinity likewise somewhat correlates with reactivity, but not perfectly since other factors are involved. For example, fluorine has a lower electron affinity than chlorine (because of extreme interelectronic repulsion for the very small fluorine atom), but is more reactive.[133]
Valence and oxidation states
The valence of an element can be defined either as the number of hydrogen atoms that can combine with it to form a simple binary hydride, or as twice the number of oxygen atoms that can combine with it to form a simple binary oxide (that is, not a peroxide or a superoxide).[110] The valences of the main-group elements are directly related to the group number: the hydrides in the main groups 1–2 and 13–17 follow the formulae MH, MH2, MH3, MH4, MH3, MH2, and finally MH. The highest oxides instead increase in valence, following the formulae M2O, MO, M2O3, MO2, M2O5, MO3, M2O7.[l] Today the notion of valence has been extended by that of the oxidation state, which is the formal charge left on an element when all other elements in a compound have been removed as their ions.[113]
The electron configuration suggests a ready explanation from the number of electrons available for bonding;[113] indeed, the number of valence electrons starts at 1 in group 1, and then increases towards the right side of the periodic table, only resetting at 3 whenever each new block starts. Thus in period 6, Cs–Ba have 1–2 valence electrons; La–Yb have 3–16; Lu–Hg have 3–12; and Tl–Rn have 3–8.[112] However, towards the right side of the d- and f-blocks, the theoretical maximum corresponding to using all valence electrons is not achievable at all;[136] the same situation affects oxygen, fluorine, and the light noble gases up to krypton.[137]
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | H 1 | He 2 | ||||||||||||||||||||||||||||||
| 2 | Li 1 | Be 2 | B 3 | C 4 | N 5 | O 6 | F 7 | Ne 8 | ||||||||||||||||||||||||
| 3 | Na 1 | Mg 2 | Al 3 | Si 4 | P 5 | S 6 | Cl 7 | Ar 8 | ||||||||||||||||||||||||
| 4 | K 1 | Ca 2 | Sc 3 | Ti 4 | V 5 | Cr 6 | Mn 7 | Fe 8 | Co 9 | Ni 10 | Cu 11 | Zn 12 | Ga 3 | Ge 4 | As 5 | Se 6 | Br 7 | Kr 8 | ||||||||||||||
| 5 | Rb 1 | Sr 2 | Y 3 | Zr 4 | Nb 5 | Mo 6 | Tc 7 | Ru 8 | Rh 9 | Pd 10 | Ag 11 | Cd 12 | In 3 | Sn 4 | Sb 5 | Te 6 | I 7 | Xe 8 | ||||||||||||||
| 6 | Cs 1 | Ba 2 | La 3 | Ce 4 | Pr 5 | Nd 6 | Pm 7 | Sm 8 | Eu 9 | Gd 10 | Tb 11 | Dy 12 | Ho 13 | Er 14 | Tm 15 | Yb 16 | Lu 3 | Hf 4 | Ta 5 | W 6 | Re 7 | Os 8 | Ir 9 | Pt 10 | Au 11 | Hg 12 | Tl 3 | Pb 4 | Bi 5 | Po 6 | At 7 | Rn 8 |
| 7 | Fr 1 | Ra 2 | Ac 3 | Th 4 | Pa 5 | U 6 | Np 7 | Pu 8 | Am 9 | Cm 10 | Bk 11 | Cf 12 | Es 13 | Fm 14 | Md 15 | No 16 | Lr 3 | Rf 4 | Db 5 | Sg 6 | Bh 7 | Hs 8 | Mt 9 | Ds 10 | Rg 11 | Cn 12 | Nh 3 | Fl 4 | Mc 5 | Lv 6 | Ts 7 | Og 8 |
A full explanation requires considering the energy that would be released in forming compounds with different valences rather than simply considering electron configurations alone.[138] For example, magnesium forms Mg2+ rather than Mg+ cations when dissolved in water, because the latter would spontaneously disproportionate into Mg0 and Mg2+ cations. This is because the enthalpy of hydration (surrounding the cation with water molecules) increases in magnitude with the charge and radius of the ion. In Mg+, the outermost orbital (which determines ionic radius) is still 3s, so the hydration enthalpy is small and insufficient to compensate the energy required to remove the electron; but ionizing again to Mg2+ uncovers the core 2p subshell, making the hydration enthalpy large enough to allow magnesium(II) compounds to form. For similar reasons, the common oxidation states of the heavier p-block elements (where the ns electrons become lower in energy than the np) tend to vary by steps of 2, because that is necessary to uncover an inner subshell and decrease the ionic radius (e.g. Tl+ uncovers 6s, and Tl3+ uncovers 5d, so once thallium loses two electrons it tends to lose the third one as well). Analogous arguments based on orbital hybridization can be used for the less electronegative p-block elements.[139][m]
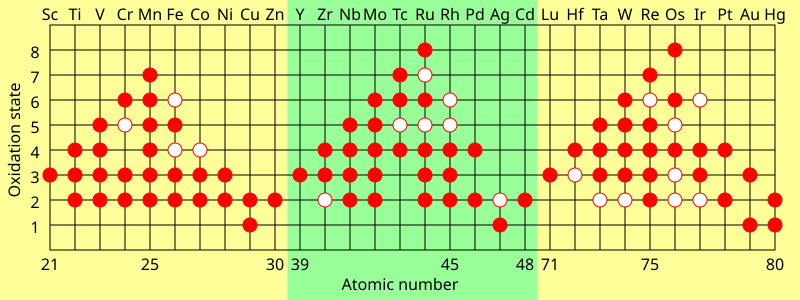
For transition metals, common oxidation states are nearly always at least +2 for similar reasons (uncovering the next subshell); this holds even for the metals with anomalous dx+1s1 or dx+2s0 configurations (except for silver), because repulsion between d-electrons means that the movement of the second electron from the s- to the d-subshell does not appreciably change its ionisation energy.[141] Because ionizing the transition metals further does not uncover any new inner subshells, their oxidation states tend to vary by steps of 1 instead.[139] The lanthanides and late actinides generally show a stable +3 oxidation state, removing the outer s-electrons and then (usually) one electron from the (n−2)f-orbitals, that are similar in energy to ns.[142] The common and maximum oxidation states of the d- and f-block elements tend to depend on the ionisation energies. As the energy difference between the (n−1)d and ns orbitals rises along each transition series, it becomes less energetically favourable to ionize further electrons. Thus, the early transition metal groups tend to prefer higher oxidation states, but the +2 oxidation state becomes more stable for the late transition metal groups. The highest formal oxidation state thus increases from +3 at the beginning of each d-block row, to +7 or +8 in the middle (e.g. OsO4), and then decrease to +2 at the end.[141] The lanthanides and late actinides usually have high fourth ionisation energies and hence rarely surpass the +3 oxidation state, whereas early actinides have low fourth ionisation energies and so for example neptunium and plutonium can reach +7.[110][141][142] The very last actinides go further than the lanthanides towards low oxidation states: mendelevium is more easily reduced to the +2 state than thulium or even europium (the lanthanide with the most stable +2 state, on account of its half-filled f-shell), and nobelium outright favours +2 over +3, in contrast to ytterbium.[54]
As elements in the same group share the same valence configurations, they usually exhibit similar chemical behaviour. For example, the alkali metals in the first group all have one valence electron, and form a very homogeneous class of elements: they are all soft and reactive metals. However, there are many factors involved, and groups can often be rather heterogeneous. For instance, hydrogen also has one valence electron and is in the same group as the alkali metals, but its chemical behaviour is quite different. The stable elements of group 14 comprise a nonmetal (carbon), two semiconductors (silicon and germanium), and two metals (tin and lead); they are nonetheless united by having four valence electrons.[143] This often leads to similarities in maximum and minimum oxidation states (e.g. sulfur and selenium in group 16 both have maximum oxidation state +6, as in SO3 and SeO3, and minimum oxidation state −2, as in sulfides and selenides); but not always (e.g. oxygen is not known to form oxidation state +6, despite being in the same group as sulfur and selenium).[58]
Electronegativity

Another important property of elements is their electronegativity. Atoms can form covalent bonds to each other by sharing electrons in pairs, creating an overlap of valence orbitals. The degree to which each atom attracts the shared electron pair depends on the atom's electronegativity[144] – the tendency of an atom towards gaining or losing electrons.[32] The more electronegative atom will tend to attract the electron pair more, and the less electronegative (or more electropositive) one will attract it less. In extreme cases, the electron can be thought of as having been passed completely from the more electropositive atom to the more electronegative one, though this is a simplification. The bond then binds two ions, one positive (having given up the electron) and one negative (having accepted it), and is termed an ionic bond.[32]
Electronegativity depends on how strongly the nucleus can attract an electron pair, and so it exhibits a similar variation to the other properties already discussed: electronegativity tends to fall going up to down, and rise going left to right. The alkali and alkaline earth metals are among the most electropositive elements, while the chalcogens, halogens, and noble gases are among the most electronegative ones.[144]
Electronegativity is generally measured on the Pauling scale, on which the most electronegative reactive atom (fluorine) is given electronegativity 4.0, and the least electronegative atom (caesium) is given electronegativity 0.79.[32] In fact neon is the most electronegative element, but the Pauling scale cannot measure its electronegativity because it does not form covalent bonds with most elements.[145]
An element's electronegativity varies with the identity and number of the atoms it is bonded to, as well as how many electrons it has already lost: an atom becomes more electronegative when it has lost more electrons.[144] This sometimes makes a large difference: lead in the +2 oxidation state has electronegativity 1.87 on the Pauling scale, while lead in the +4 oxidation state has electronegativity 2.33.[146]
Metallicity

(In grey tin, the band gap vanishes and metallization occurs.[147] Tin has another allotrope, white tin, whose structure is even more metallic.)
A simple substance is a substance formed from atoms of one chemical element. The simple substances of the more electronegative atoms tend to share electrons (form covalent bonds) with each other. They form either small molecules (like hydrogen or oxygen, whose atoms bond in pairs) or giant structures stretching indefinitely (like carbon or silicon). The noble gases simply stay as single atoms, as they already have a full shell.[32] Substances composed of discrete molecules or single atoms are held together by weaker attractive forces between the molecules, such as the London dispersion force: as electrons move within the molecules, they create momentary imbalances of electrical charge, which induce similar imbalances on nearby molecules and create synchronized movements of electrons across many neighbouring molecules.[148]

The more electropositive atoms, however, tend to instead lose electrons, creating a "sea" of electrons engulfing cations.[32] The outer orbitals of one atom overlap to share electrons with all its neighbours, creating a giant structure of molecular orbitals extending over all the atoms.[149] This negatively charged "sea" pulls on all the ions and keeps them together in a metallic bond. Elements forming such bonds are often called metals; those which do not are often called nonmetals.[32] Some elements can form multiple simple substances with different structures: these are called allotropes. For example, diamond and graphite are two allotropes of carbon.[143][n]
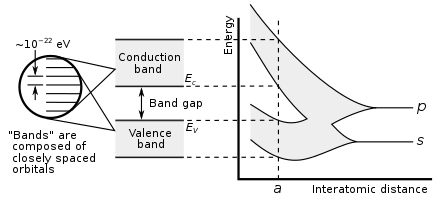
The metallicity of an element can be predicted from electronic properties. When atomic orbitals overlap during metallic or covalent bonding, they create both bonding and antibonding molecular orbitals of equal capacity, with the antibonding orbitals of higher energy. Net bonding character occurs when there are more electrons in the bonding orbitals than there are in the antibonding orbitals. Metallic bonding is thus possible when the number of electrons delocalized by each atom is less than twice the number of orbitals contributing to the overlap. This is the situation for elements in groups 1 through 13; they also have too few valence electrons to form giant covalent structures where all atoms take equivalent positions, and so almost all of them metallise. The exceptions are hydrogen and boron, which have too high an ionisation energy. Hydrogen thus forms a covalent H2 molecule, and boron forms a giant covalent structure based on icosahedral B12 clusters. In a metal, the bonding and antibonding orbitals have overlapping energies, creating a single band that electrons can freely flow through, allowing for electrical conduction.[151]


 French
French Deutsch
Deutsch
