Polar circle

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Polar circle" – news · newspapers · books · scholar · JSTOR (December 2016) (Learn how and when to remove this message)

A polar circle is a geographic term for a conditional circular line (arc) referring either to the Arctic Circle or the Antarctic Circle. These are two of the keynote circles of latitude (parallels). On Earth, the Arctic Circle is currently drifting northwards at a speed of about 14.5 m per year and is now at a mean latitude (i.e. without taking into account the astronomical nutation) of 66°33′50.2″ N; the Antarctic Circle is currently drifting southwards at a speed of about 14.5 m per year and is now at a mean latitude of 66°33′50.2″ S.^[1] Polar circles are often equated with polar regions of Earth. Due to their inherent climate environment, the bulk of the Arctic Circle, much of which is sea, is sparsely settled whereas this applies to all of Antarctica which is mainly land and sheltered ice shelves.

If Earth had no atmosphere, then both polar circles (arcs) would see at least a day a year when the center of the Sun is continuously above the horizon and at least a day a year when it is always below the horizon – a polar day and a polar night as is the case for longer, within the circles. Up to and including the associated poles (North and South), known geographically as the frigid zones, such duration extends up to half of the year, namely, close to the poles. Instead, atmospheric refraction and the Sun's light reaching the planet as an extended object rather than a point source means that just within each circle the Earth's surface does not experience any proper polar night, 24 hours where the sun does not rise. By these same two factors, just outward of each circle still experiences a polar day (a day in which the sun does not fully set).

The latitude of the polar circles is + or −90 degrees (which refers to the North and South Pole, respectively) minus the axial tilt (that is, of the Earth's axis of daily rotation relative to the ecliptic, the plane of the Earth's orbit). This predominant, average tilt of the Earth varies slightly, a phenomenon described as nutation. Therefore, the latitudes noted above are calculated by averaging values of tilt observed over many years. The axial tilt also exhibits long-term variations as described in the reference article (a difference of 1 second of arc (″) in the tilt is equivalent to a change of about 31 metres north or south in the positions of the polar circles on the Earth's surface).

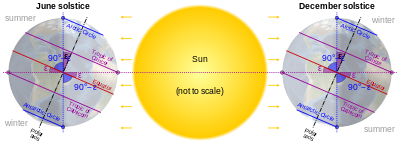
The polar circles would almost precisely match the boundaries for the zones where the polar night and the polar day would occur throughout the winter solstice and summer solstice day respectively. They do so loosely due to two effects. The first one is atmospheric refraction, in which the Earth's atmosphere bends light rays near the horizon. The second effect is caused by the angular diameter of the Sun as seen from the Earth's orbital distance (which varies very slightly during each orbit). These factors mean the ground-observed boundaries are 80 to 100 kilometres (50 to 62 mi) away from the circle.^{[citation needed]} A further global factor for this numerical range is Earth's nutation, which is a very small change in tilt. Observers higher above sea level can see a tiny amount of the Sun's disc (see horizon) where at lower places it would not rise. For the Arctic Circle, being 80–100 km north of the circle in winter, and 80–100 km south of the circle in summer; the inverse directions apply to the other circle.^[2]

• Antarctica
• Antarctic Circle
• Arctic
• Arctic Circle
• Frigid zones
• Polar climate
• Polar day and Polar night
• Polar region