Hardness

In materials science, hardness (antonym: softness) is a measure of the resistance to localized plastic deformation, such as an indentation (over an area) or a scratch (linear), induced mechanically either by pressing or abrasion. In general, different materials differ in their hardness; for example hard metals such as titanium and beryllium are harder than soft metals such as sodium and metallic tin, or wood and common plastics. Macroscopic hardness is generally characterized by strong intermolecular bonds, but the behavior of solid materials under force is complex; therefore, hardness can be measured in different ways, such as scratch hardness, indentation hardness, and rebound hardness. Hardness is dependent on ductility, elastic stiffness, plasticity, strain, strength, toughness, viscoelasticity, and viscosity. Common examples of hard matter are ceramics, concrete, certain metals, and superhard materials, which can be contrasted with soft matter.

There are three main types of hardness measurements: scratch, indentation, and rebound. Within each of these classes of measurement there are individual measurement scales. For practical reasons conversion tables are used to convert between one scale and another.

Scratch hardness is the measure of how resistant a sample is to fracture or permanent plastic deformation due to friction from a sharp object.^[1] The principle is that an object made of a harder material will scratch an object made of a softer material. When testing coatings, scratch hardness refers to the force necessary to cut through the film to the substrate. The most common test is Mohs scale, which is used in mineralogy. One tool to make this measurement is the sclerometer.

Another tool used to make these tests is the pocket hardness tester. This tool consists of a scale arm with graduated markings attached to a four-wheeled carriage. A scratch tool with a sharp rim is mounted at a predetermined angle to the testing surface. In order to use it a weight of known mass is added to the scale arm at one of the graduated markings, the tool is then drawn across the test surface. The use of the weight and markings allows a known pressure to be applied without the need for complicated machinery.^[2]

Indentation hardness measures the resistance of a sample to material deformation due to a constant compression load from a sharp object. Tests for indentation hardness are primarily used in engineering and metallurgy. The tests work on the basic premise of measuring the critical dimensions of an indentation left by a specifically dimensioned and loaded indenter. Common indentation hardness scales are Rockwell, Vickers, Shore, and Brinell, amongst others.

Rebound hardness, also known as dynamic hardness, measures the height of the "bounce" of a diamond-tipped hammer dropped from a fixed height onto a material. This type of hardness is related to elasticity. The device used to take this measurement is known as a scleroscope.^[3] Two scales that measures rebound hardness are the Leeb rebound hardness test and Bennett hardness scale. Ultrasonic Contact Impedance (UCI) method determines hardness by measuring the frequency of an oscillating rod. The rod consists of a metal shaft with vibrating element and a pyramid-shaped diamond mounted on one end.^[4]

There are five hardening processes: Hall-Petch strengthening, work hardening, solid solution strengthening, precipitation hardening, and martensitic transformation.

In solid mechanics, solids generally have three responses to force, depending on the amount of force and the type of material:

• They exhibit elasticity—the ability to temporarily change shape, but return to the original shape when the pressure is removed. "Hardness" in the elastic range—a small temporary change in shape for a given force—is known as stiffness in the case of a given object, or a high elastic modulus in the case of a material.
• They exhibit plasticity—the ability to permanently change shape in response to the force, but remain in one piece. The yield strength is the point at which elastic deformation gives way to plastic deformation. Deformation in the plastic range is non-linear, and is described by the stress-strain curve. This response produces the observed properties of scratch and indentation hardness, as described and measured in materials science. Some materials exhibit both elasticity and viscosity when undergoing plastic deformation; this is called viscoelasticity.
• They fracture—split into two or more pieces.

Strength is a measure of the extent of a material's elastic range, or elastic and plastic ranges together. This is quantified as compressive strength, shear strength, tensile strength depending on the direction of the forces involved. Ultimate strength is an engineering measure of the maximum load a part of a specific material and geometry can withstand.

Brittleness, in technical usage, is the tendency of a material to fracture with very little or no detectable plastic deformation beforehand. Thus in technical terms, a material can be both brittle and strong. In everyday usage "brittleness" usually refers to the tendency to fracture under a small amount of force, which exhibits both brittleness and a lack of strength (in the technical sense). For perfectly brittle materials, yield strength and ultimate strength are the same, because they do not experience detectable plastic deformation. The opposite of brittleness is ductility.

The toughness of a material is the maximum amount of energy it can absorb before fracturing, which is different from the amount of force that can be applied. Toughness tends to be small for brittle materials, because elastic and plastic deformations allow materials to absorb large amounts of energy.

Hardness increases with decreasing particle size. This is known as the Hall-Petch relationship. However, below a critical grain-size, hardness decreases with decreasing grain size. This is known as the inverse Hall-Petch effect.

Hardness of a material to deformation is dependent on its microdurability or small-scale shear modulus in any direction, not to any rigidity or stiffness properties such as its bulk modulus or Young's modulus. Stiffness is often confused for hardness.^[5][6] Some materials are stiffer than diamond (e.g. osmium) but are not harder, and are prone to spalling and flaking in squamose or acicular habits.

The key to understanding the mechanism behind hardness is understanding the metallic microstructure, or the structure and arrangement of the atoms at the atomic level. In fact, most important metallic properties critical to the manufacturing of today’s goods are determined by the microstructure of a material.^[7] At the atomic level, the atoms in a metal are arranged in an orderly three-dimensional array called a crystal lattice. In reality, however, a given specimen of a metal likely never contains a consistent single crystal lattice. A given sample of metal will contain many grains, with each grain having a fairly consistent array pattern. At an even smaller scale, each grain contains irregularities.

There are two types of irregularities at the grain level of the microstructure that are responsible for the hardness of the material. These irregularities are point defects and line defects. A point defect is an irregularity located at a single lattice site inside of the overall three-dimensional lattice of the grain. There are three main point defects. If there is an atom missing from the array, a vacancy defect is formed. If there is a different type of atom at the lattice site that should normally be occupied by a metal atom, a substitutional defect is formed. If there exists an atom in a site where there should normally not be, an interstitial defect is formed. This is possible because space exists between atoms in a crystal lattice. While point defects are irregularities at a single site in the crystal lattice, line defects are irregularities on a plane of atoms. Dislocations are a type of line defect involving the misalignment of these planes. In the case of an edge dislocation, a half plane of atoms is wedged between two planes of atoms. In the case of a screw dislocation two planes of atoms are offset with a helical array running between them.^[8]

In glasses, hardness seems to depend linearly on the number of topological constraints acting between the atoms of the network.^[9] Hence, the rigidity theory has allowed predicting hardness values with respect to composition.

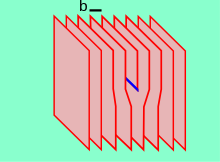
Dislocations provide a mechanism for planes of atoms to slip and thus a method for plastic or permanent deformation.^[7] Planes of atoms can flip from one side of the dislocation to the other effectively allowing the dislocation to traverse through the material and the material to deform permanently. The movement allowed by these dislocations causes a decrease in the material's hardness.

The way to inhibit the movement of planes of atoms, and thus make them harder, involves the interaction of dislocations with each other and interstitial atoms. When a dislocation intersects with a second dislocation, it can no longer traverse through the crystal lattice. The intersection of dislocations creates an anchor point and does not allow the planes of atoms to continue to slip over one another^[10] A dislocation can also be anchored by the interaction with interstitial atoms. If a dislocation comes in contact with two or more interstitial atoms, the slip of the planes will again be disrupted. The interstitial atoms create anchor points, or pinning points, in the same manner as intersecting dislocations.

By varying the presence of interstitial atoms and the density of dislocations, a particular metal's hardness can be controlled. Although seemingly counter-intuitive, as the density of dislocations increases, there are more intersections created and consequently more anchor points. Similarly, as more interstitial atoms are added, more pinning points that impede the movements of dislocations are formed. As a result, the more anchor points added, the harder the material will become.

Careful note should be taken of the relationship between a hardness number and the stress-strain curve exhibited by the material. The latter, which is conventionally obtained via tensile testing, captures the full plasticity response of the material (which is in most cases a metal). It is in fact a dependence of the (true) von Mises plastic strain on the (true) von Mises stress, but this is readily obtained from a nominal stress – nominal strain curve (in the pre-necking regime), which is the immediate outcome of a tensile test. This relationship can be used to describe how the material will respond to almost any loading situation, often by using the Finite Element Method (FEM). This applies to the outcome of an indentation test (with a given size and shape of indenter, and a given applied load).

However, while a hardness number thus depends on the stress-strain relationship, inferring the latter from the former is far from simple and is not attempted in any rigorous way during conventional hardness testing. (In fact, the Indentation Plastometry technique, which involves iterative FEM modelling of an indentation test, does allow a stress-strain curve to be obtained via indentation, but this is outside the scope of conventional hardness testing.) A hardness number is just a semi-quantitative indicator of the resistance to plastic deformation. Although hardness is defined in a similar way for most types of test – usually as the load divided by the contact area – the numbers obtained for a particular material are different for different types of test, and even for the same test with different applied loads. Attempts are sometimes made^{[11][12][13][14][15]} to identify simple analytical expressions that allow features of the stress-strain curve, particularly the yield stress and Ultimate Tensile Stress (UTS), to be obtained from a particular type of hardness number. However, these are all based on empirical correlations, often specific to particular types of alloy: even with such a limitation, the values obtained are often quite unreliable. The underlying problem is that metals with a range of combinations of yield stress and work hardening characteristics can exhibit the same hardness number. The use of hardness numbers for any quantitative purpose should, at best, be approached with considerable caution.

• Chinn, R. L. (2009). "Hardness, bearings, and the Rockwells". Advanced Materials & Processes. 167 (10): 29–31.
• Davis, J. R. (Ed.). (2002). Surface hardening of steels: Understanding the basics. Materials Park, OH: ASM International.
• Dieter, George E. (1989). Mechanical Metallurgy. SI Metric Adaptation. Maidenhead, UK: McGraw-Hill Education. ISBN 0-07-100406-8
• Malzbender, J (2003). "Comment on hardness definitions". Journal of the European Ceramic Society. 23 (9): 9. doi:10.1016/S0955-2219(02)00354-0.
• Revankar, G. (2003). "Introduction to hardness testing." Mechanical testing and evaluation, ASM Online Vol. 8.

Look up hardness in Wiktionary, the free dictionary.

• An introduction to materials hardness
• Guidelines to hardness testing Archived 2021-02-25 at the Wayback Machine
• Testing the Hardness of Metals