Circuncentro , la enciclopedia libre

El circuncentro de un triángulo es el punto en el que se cortan las mediatrices de sus tres lados.^[1]​^[2]​^[3]​^[4]​ ^[5]​

El circuncentro es también el centro de la circunferencia circunscrita al triángulo, ya que es equidistante a los tres vértices del mismo. El radio de dicha circunferencia se denomina circunradio, y puede calcularse como la distancia del circuncentro a cualquiera de los vértices del triángulo.

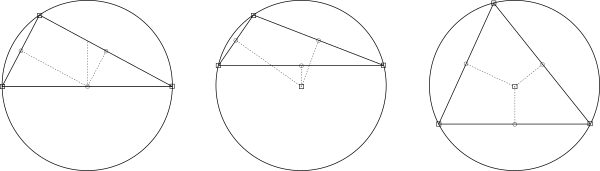
En formulación matemática el circuncentro suele denominarse con la letra O, mientras que el circunradio suele denominarse con la letra R.

• El circuncentro de un triángulo puede ser interior o exterior al mismo, dependiendo de su clasificación por ángulos:
  • Si el triángulo rectángulo, el circuncentro se sitúa en el punto medio de la hipotenusa.
  • Si el triángulo obtusángulo, el circuncentro será exterior al triángulo.
  • Si el triángulo acutángulo, el circuncentro es interior al triángulo.

• El circuncentro, el baricentro y el ortocentro de un triángulo están siempre alineados, y forman parte de la Recta de Euler.
• El diámetro de la circunferencia circunscrita es igual a la longitud de cualquiera de los lados dividida por el seno del ángulo opuesto. Esto relaciona el circunradio de un triángulo directamente con el teorema de los senos, cumpliéndose que ${\displaystyle 2R={\frac {a}{\operatorname {sen} {\widehat {A}}}}={\frac {b}{\operatorname {sen} {\widehat {B}}}}={\frac {c}{\operatorname {sen} {\widehat {C}}}}\,}$.
• El circunradio está relacionado con el área ${\displaystyle S}$ del triángulo, cumpliéndose que ${\displaystyle R={\dfrac {abc}{4S}}\,}$.
• El circunradio también está relacionado con el radio de la circunferencia inscrita de un triángulo ${\displaystyle r}$ mediante varias fórmulas, cumpliéndose que:

${\displaystyle R={\frac {abc}{2r(a+b+c)}}={\frac {r}{cosA+cosB+cosC-1}}={\sqrt {\frac {a^{2}+b^{2}+c^{2}}{8(1+cosA\,cosB\,cosC)}}}\,}$.

• Recta de Euler
• Ortocentro
• Baricentro
• Incentro