Espiral , la enciclopedia libre

Una espiral es una línea curva generada por un punto que se va alejando progresivamente del centro a la vez que gira alrededor de él.^[1]​ Normalmente se define con una función que depende de dos valores: el ángulo del punto respecto a un eje de referencia, y la distancia desde este punto al centro, situado en el vértice del ángulo.

En el video musical del aniversario 20 de Cartoon Network, hay una parte en que Arcoiris de Adventure Time se envuelve en una larga espiral de Arquímedes en el cielo mientras está durmiendo en un mundo en blanco y negro.

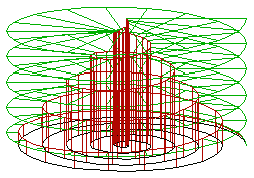
«Espiral» y «hélice» son dos vocablos que se confunden fácilmente. Una espiral suele ser plana (como el surco de un disco de vinilo). Una hélice, en cambio, siempre es tridimensional: es una línea curva continua, con pendiente finita y no nula, que gira alrededor de un cilindro, un cono o una esfera, avanzando en las tres dimensiones (como el borde de un tornillo).

Las espirales bidimensionales más conocidas son:

• La espiral de Arquímedes: r = a + bθ
• La espiral clotoide
• La espiral de Fermat: r = θ^1/2
• La espiral hiperbólica: r = a/θ
• La espiral logarítmica: ${\displaystyle \theta =\log _{b}(r/a)\,}$
• 
  Espiral de Arquímedes
• 
  Espiral logarítmica
• 
  Espiral de Fermat
• 
  espiral hiperbólica

Para la creación de espirales tridimensionales se introduce una variable más en la función de la espiral, cuyo valor es el de una función continua y de monotonía repetitiva que depende del ángulo.

Una hélice esférica, también llamada espiral esférica, es la curva que describiría un «barco ideal» viajando desde un polo hasta el otro polo de la Tierra, manteniendo una misma pendiente finita no nula. La hélice tendría un número infinito de revoluciones, con la distancia entre ellas cada vez menor a medida que se acercara a los polos.

La única forma de evitar dar vueltas indefinidamente en una hélice esférica es que esta fuera arquimediana; es decir, que la pendiente del barco se ajustara a la necesaria para que la función de dicha hélice coincidiera con la de la espiral arquimediana sobre la esfera.

La espiral es uno de los símbolos más antiguos y se encuentra en todos los continentes, habiendo jugado un papel fundamental en el simbolismo desde su aparición en el arte megalítico.

Parece que en muchos lugares representaba el ciclo «nacimiento-muerte-renacimiento» así como al Sol, que se creía seguía ese mismo ciclo, naciendo cada mañana, muriendo cada noche y renaciendo a la mañana siguiente.

Actualmente, la espiral también es empleada como símbolo para representar el pensamiento cíclico, en diversas propuestas filosóficas, espirituales, estéticas y tecnológicas, por lo que puede hablarse en rigor de cierto espiralismo o concepción espiralista, como refleja el arte del escultor canario Martín Chirino o el pintor cubano Ángel Laborde Wilson.

El estudio de las espirales en la naturaleza tiene una larga historia que se remonta a Christopher Wren, quien observó que muchas conchas animales formaban una espiral logarítmica. Jan Swammerdam observó las características comunes de un amplio abanico de conchas, desde la Helix hasta la Spirula, y Henry Nottidge Moseley describió la geometría de las conchas de los Gastropoda. En Sobre el crecimiento y la forma,^[2]​ D'Arcy Wentworth Thompson examina exhaustivamente estas espirales. Describe cómo las conchas se forman siguiendo una curva que rota en torno a un eje, de modo que la forma de la curva permanece constante pero su tamaño aumenta en progresión geométrica. En algunas conchas como nautilus y las amonites la curva generatriz gira en un plano perpendicular al eje y la concha se conforma como figura discoidal plana. En otras sigue un patrón espacial, con forma de hélice. Thompson también estudió la aparición de espirales en la anatomía de diversos cuernos, pelambres, dientes, uñas y algunas plantas. La isla de Célebes, en el Pacífico, nos da una idea de figura en espiral.

• Loxodrómica
• Hélice
• Coordenadas polares
• Evolvente

• Cook, T., 1903. Spirals in nature and art. Nature 68 (1761), 296.
• Cook, T., 1979. The curves of life. Dover, New York.
• Habib, Z., Sakai, M., 2005. Spiral transition curves and their applications. Scientiae Mathematicae Japonicae 61 (2), 195 – 206.
• Dimulyo, S., Habib, Z., Sakai, M., 2009. Fair cubic transition between two circles with one circle inside or tangent to the other. Numerical Algorithms 51, 461–476 [1] Archivado el 27 de noviembre de 2018 en Wayback Machine..
• Harary, G., Tal, A., 2011. The natural 3D spiral. Computer Graphics Forum 30 (2), 237 – 246 [2].
• Xu, L., Mould, D., 2009. Magnetic curves: curvature-controlled aesthetic curves using magnetic fields. In: Deussen, O., Hall, P. (Eds.), Computational Aesthetics in Graphics, Visualization, and Imaging. The Eurographics Association [3].
• Wang, Y., Zhao, B., Zhang, L., Xu, J., Wang, K., Wang, S., 2004. Designing fair curves using monotone curvature pieces. Computer Aided Geometric Design 21 (5), 515–527 [4].
• A. Kurnosenko. Applying inversion to construct planar, rational spirals that satisfy two-point G2 Hermite data. Computer Aided Geometric Design, 27(3), 262-280, 2010 [5].
• A. Kurnosenko. Two-point G2 Hermite interpolation with spirals by inversion of hyperbola. Computer Aided Geometric Design, 27(6), 474-481, 2010.
• Miura, K.T., 2006. A general equation of aesthetic curves and its self-affinity. Computer-Aided Design and Applications 3 (1–4), 457–464 [6].
• Miura, K., Sone, J., Yamashita, A., Kaneko, T., 2005. Derivation of a general formula of aesthetic curves. In: 8th International Conference on Humans and Computers (HC2005). Aizu-Wakamutsu, Japan, pp. 166 – 171 [7].
• Meek, D., Walton, D., 1989. The use of Cornu spirals in drawing planar curves of controlled curvature. Journal of Computational and Applied Mathematics 25 (1), 69–78 [8].
• Farin, G., 2006. Class A Bézier curves. Computer Aided Geometric Design 23 (7), 573–581 [9].
• Farouki, R.T., 1997. Pythagorean-hodograph quintic transition curves of monotone curvature. Computer-Aided Design 29 (9), 601–606.
• Yoshida, N., Saito, T., 2006. Interactive aesthetic curve segments. The Visual Computer 22 (9), 896–905 [10] Archivado el 4 de marzo de 2016 en Wayback Machine..
• Yoshida, N., Saito, T., 2007. Quasi-aesthetic curves in rational cubic Bézier forms. Computer-Aided Design and Applications 4 (9–10), 477–486 [11] Archivado el 3 de marzo de 2016 en Wayback Machine..
• Ziatdinov, R., Yoshida, N., Kim, T., 2012. Analytic parametric equations of log-aesthetic curves in terms of incomplete gamma functions. Computer Aided Geometric Design 29 (2), 129 – 140 [12].
• Ziatdinov, R., Yoshida, N., Kim, T., 2012. Fitting G2 multispiral transition curve joining two straight lines, Computer-Aided Design 44(6), 591–596 [13].
• Ziatdinov, R., 2012. Family of superspirals with completely monotonic curvature given in terms of Gauss hypergeometric function. Computer Aided Geometric Design 29(7): 510-518 [14].
• Ziatdinov, R., Miura K.T., 2012. On the Variety of Planar Spirals and Their Applications in Computer Aided Design. European Researcher 27(8-2), 1227-1232 [15].

• Curvas Técnicas y Cíclicas por José Antonio Cuadrado (15/5/12)
• Wikimedia Commons alberga una galería multimedia sobre Espiral.