Homología (matemática) , la enciclopedia libre

En matemática (especialmente en topología algebraica y en álgebra homológica), la homología (en Griego homos = idéntico) es un procedimiento general para asociar un objeto matemático dado (por ejemplo un espacio topológico o un grupo) con una sucesión de grupos abelianos (o en contextos más generales módulos o cualquier elemento sobre una categoría abeliana), es decir una acción functorial.

Para un espacio topológico, los grupos de homología son generalmente mucho más fáciles de computar que los grupos de homotopía, y consecuentemente, uno habitualmente tendrá un trabajo más simple con homología para ayudar en la clasificación de espacios.

Una observación que motiva esta teoría es que a veces podemos distinguir parejas de espacios topológicos, por medio del estudio de sus agujeros. Por ejemplo:

• Un círculo no es equivalente a un disco porque el círculo tiene un agujero en medio de él.
• Una esfera no es equivalente a un círculo, ya que la esfera encierra un agujero 2-dimensional, mientras que el círculo encierra un agujero 1-dimensional.

En general, no es inmediato ni definir lo que es un agujero, ni distinguir distintos tipos de agujeros. Es por ello que la motivación original de homología fue definir y clasificar los agujeros de un espacio topológico, por ejemplo en una variedad.

La definición de los grupos de homología se fundamenta en los conceptos de ciclos, - que son subvariedades cerradas - fronteras, -que son ciclos y a la vez fronteras de una subvariedad-, y clases de homología -que son las clases de equivalencia que obtenemos al cocientar los ciclos módulo las fronteras. Entonces, cada clase de homología está representada por un ciclo que no es frontera de ninguna subvariedad, e indica la ausencia de una variedad cuya frontera sería dicho ciclo. Así mismo, cada generador indica la existencia de un agujero y las propiedades del grupo indican la estructura del espacio topológico, así como lo hacen las nociones de dimensión y orientabilidad.

Existen diferentes teorías de homología. Dependiendo del objeto matemático que estemos estudiando - por ejemplo, un espacio topológico o un grupo-, podremos asociarle algunas de estas teorías. Cuando podemos describir geométricamente a dicho objeto, el n-avo grupo de homología describe el comportamiento del objeto en la n-ava dimensión.

Puede decirse que la teoría de la homología comienza con la fórmula del poliedro de Euler, o característica de Euler.^[1]​ Esto fue seguido por la definición de Riemann de invariantes numéricos de género y conexión de 'n' veces en 1857 y la prueba de Betti en 1871 de la independencia de los "números de homología" de la elección de la base.^[2]​

La propia homología se desarrolló como una forma de analizar y clasificar variedades según sus ciclos - bucles cerrados (o más generalmente submanifolds) que se pueden dibujar en una determinada n manifold dimensional pero que no se deforman continuamente entre sí.^[3]​ Estos ciclos también se consideran a veces como cortes que se pueden volver a pegar, o como cremalleras que se pueden abrochar y desabrochar. Los ciclos se clasifican por dimensiones. Por ejemplo, una línea trazada sobre una superficie representa un 1-ciclo, un bucle cerrado o ${\displaystyle S^{1}}$ (1-variedad), mientras que una superficie cortada a través de una variedad tridimensional es un 2-ciclo.

Ciclos en 2 esferas

Ciclos en un toro

Ciclos en una botella de Klein

Ciclos en un plano proyectivo hemisférico

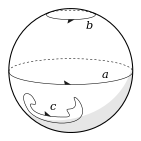
En la esfera ordinaria ${\displaystyle S^{2}}$, el ciclo b del diagrama puede reducirse hasta el polo, e incluso el gran círculo ecuatorial a puede reducirse del mismo modo. El teorema de la curva de Jordan muestra que cualquier ciclo arbitrario como c puede reducirse de forma similar hasta un punto. Por tanto, todos los ciclos de la esfera pueden transformarse continuamente unos en otros y pertenecen a la misma clase homológica. Se dice que son homólogos a cero. Cortar una variedad a lo largo de un ciclo homólogo a cero separa la variedad en dos o más componentes. Por ejemplo, cortar la esfera a lo largo de a produce dos hemisferios.

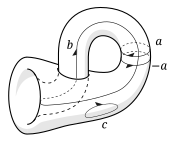
Esto no suele ocurrir con los ciclos de otras superficies. El toroide ${\displaystyle T^{2}}$ tiene ciclos que no pueden deformarse continuamente unos en otros, por ejemplo en el diagrama ninguno de los ciclos a, b o c puede deformarse uno en otro. En particular, los ciclos a y b no pueden reducirse a un punto, mientras que el ciclo c sí puede, lo que lo hace homólogo a cero.

Si la superficie del toro se corta a lo largo de a y b, puede abrirse y aplanarse en un rectángulo o, más convenientemente, en un cuadrado. Un par de lados opuestos representa el corte a lo largo de a, y el otro par opuesto representa el corte a lo largo de b.

A continuación, los bordes del cuadrado se pueden pegar de diferentes maneras. El cuadrado se puede girar para que los bordes se junten en la dirección opuesta, como muestran las flechas del diagrama. Hasta la simetría, hay cuatro formas distintas de pegar los lados, cada una de las cuales crea una superficie diferente:

.

${\displaystyle K^{2}}$ es la botella de Klein, que es un toro con una torsión en él (La torsión se puede véase en el diagrama cuadrado como la inversión de la flecha inferior). Es un teorema que la superficie re-encolada debe auto-intersecarse (cuando se sumerge en el espacio euclidiano tridimensional). Al igual que el toroide, los ciclos a y b no pueden encogerse, mientras que c sí. Pero, a diferencia del toro, si se sigue b hacia delante y hacia atrás, se invierte a izquierda y derecha, porque b cruza el giro dado a una de las uniones. Si se hace un corte equidistante a un lado de b, vuelve por el otro lado y recorre la superficie una segunda vez antes de volver a su punto de partida, cortando una banda de Möbius retorcida. Dado que la izquierda y la derecha locales pueden reorientarse arbitrariamente de este modo, se dice que la superficie en su conjunto no es orientable.

El plano proyectivo ${\displaystyle P^{2}}$ tiene ambas uniones torcidas. La forma sin cortar, generalmente representada como la superficie de Boy, es visualmente compleja, por lo que en el diagrama se muestra una incrustación semiesférica, en la que puntos antípodas alrededor del borde como A y A′ se identifican como el mismo punto. De nuevo, a y b no son encogibles, mientras que c sí lo es. Pero esta vez, tanto a como b se invierten a izquierda y derecha.

Los ciclos pueden unirse o sumarse, como ocurrió con a y b en el toroide cuando se abrió y aplanó. En el diagrama de la botella de Klein, a gira en un sentido y −a gira en sentido contrario. Si a se considera un corte, entonces -a puede considerarse una operación de encolado. Hacer un corte y luego volverlo a pegar no cambia la superficie, así que a + (-a) = 0.

Pero consideremos ahora dos ciclos a. Como la botella de Klein no es orientable, podemos transportar uno de ellos alrededor de la botella (a lo largo del ciclo b), y volverá como -a. Esto se debe a que la botella de Klein está hecha de un cilindro, cuyos extremos del ciclo a están pegados con orientaciones opuestas. Por lo tanto 2a = a + a = a + (-a) = 0. Este fenómeno se llama torsión. Análogamente, en el plano proyectivo, seguir dos veces el ciclo no reducible b crea notablemente un ciclo trivial que puede ser reducido a un punto; es decir, b + b = 0. Dado que b debe seguirse dos veces para conseguir un ciclo cero, se dice que la superficie tiene un coeficiente de torsión de 2. Sin embargo, seguir un ciclo b dos veces en la botella de Klein da simplemente b + b = 2b, ya que este ciclo vive en una clase homológica libre de torsión. Esto corresponde al hecho de que en el polígono fundamental de la botella de Klein, sólo un par de lados está pegado con una torsión, mientras que en el plano proyectivo ambos lados están torcidos.

Un cuadrado es un espacio topológico contráctil, lo que implica que tiene homología trivial. En consecuencia, los cortes adicionales lo desconectan. El cuadrado no es la única forma del plano que puede pegarse en una superficie. Pegando lados opuestos de un octógono, por ejemplo, se obtiene una superficie con dos agujeros. De hecho, todas las superficies cerradas pueden producirse pegando los lados de algún polígono y todos los polígonos de lados pares (2n-gonos) pueden pegarse para formar diferentes colectores. A la inversa, una superficie cerrada con n clases distintas de cero puede cortarse en un 2n-gono. También son posibles variaciones, por ejemplo, un hexágono también puede pegarse para formar un toroide.^[4]​

La primera teoría reconocible de la homología fue publicada por Henri Poincaré en su trabajo seminal "Analysis situs", J. Ecole polytech. (2) 1. 1-121 (1895). El artículo introduce las clases y relaciones homológicas. Las posibles configuraciones de los ciclos orientables se clasifican por los números de Betti del colector (los números de Betti son un refinamiento de la característica de Euler). La clasificación de los ciclos no orientables requiere información adicional sobre los coeficientes de torsión.^[3]​

La clasificación completa de 1- y 2-manifolds se da en la tabla.

Características topológicas de 1- y 2-manifolds cerrados y no acotados^[5]​

Manifold		Euler no., χ	Orientabilidad	Número de Betti			Coeficiente de torsión (1-dimensional)
Símbolo[4]​	Nombre			b0	b1	b2
${\displaystyle S^{1}}$	Círculo (1-manifold)	0	Orientable	1	1
${\displaystyle S^{2}}$	Esfera	2	Orientable	1	0	1	No
${\displaystyle T^{2}}$	Toro	0	Orientable	1	2	1	No
${\displaystyle P^{2}}$	Plano proyectivo	1	Non-orientable	1	0	0	2
${\displaystyle K^{2}}$	Botella de Klein	0	Non-orientable	1	1	0	2
	toroide de 2 agujeros	−2	Orientable	1	4	1	No
	toroide con g agujeros (g es el género)	2 − 2g	Orientable	1	2g	1	No
	Esfera con c cross-caps	2 − c	No-orientable	1	c − 1	0	2
	2-Manifold con g agujeros y c tapas cruzadas (c > 0)	2 − (2g + c)	No-orientable	1	(2g + c) − 1	0	2

Notas

1. Para una superficie no orientable, un agujero equivale a dos tapas cruzadas.
2. Todo 2-manifold es la suma conexa de toros g y planos proyectivos c. Para la esfera ${\displaystyle S^{2}}$, g = c = 0.

Un colector con límite o colector abierto es topológicamente distinto de un colector cerrado y puede crearse haciendo un corte en cualquier colector cerrado adecuado. Por ejemplo, el disco o 2-ball ${\displaystyle B^{2}}$ está limitado por un círculo ${\displaystyle S^{1}}$.^{[cita requerida]} Puede crearse cortando un ciclo trivial en cualquier 2-manifold y manteniendo el trozo eliminado, perforando la esfera y estirando la punción a lo ancho, o cortando el plano proyectivo. También puede verse como el relleno del círculo en el plano.

Cuando dos ciclos pueden deformarse continuamente el uno en el otro, entonces el corte a lo largo de uno produce la misma forma que el corte a lo largo del otro, hasta cierta flexión y estiramiento. En este caso se dice que los dos ciclos son

• homólogos

o que pertenecen a la

• misma clase de homología.

Además, si un ciclo se puede deformar continuamente en una combinación de otros ciclos, entonces el corte a lo largo del ciclo inicial es el mismo que el corte a lo largo de la combinación de otros ciclos. Por ejemplo, cortar a lo largo de una figura 8 es equivalente a cortar a lo largo de sus dos lóbulos. En este caso, se dice que la figura 8 es homóloga a la suma de sus lóbulos.

Dos colectores abiertos con límites similares (hasta cierto grado de flexión y estiramiento) pueden pegarse para formar un nuevo colector que es su suma conexa.

Este análisis geométrico de los manifolds no es riguroso. En una búsqueda de mayor rigor, Poincaré pasó a desarrollar la homología simplicial de una variedad triangulada y a crear lo que ahora se denomina un complejo en cadena.^[6]​^[7]​ Estos complejos en cadena (desde entonces muy generalizados) forman la base de la mayoría de los tratamientos modernos de la homología.

En estos tratamientos, un ciclo no tiene por qué ser continuo: un ciclo 0 es un conjunto de puntos, y cortar a lo largo de este ciclo corresponde a perforar la variedad. Un ciclo 1 corresponde a un conjunto de bucles cerrados (una imagen del manifold 1 ${\displaystyle S^{1}}$). En una superficie, el corte a lo largo de un 1-ciclo produce piezas desconectadas o una forma más simple. Un 2-ciclo corresponde a una colección de superficies incrustadas, como una esfera o un toroide, y así sucesivamente.

Emmy Noether e, independientemente, Leopold Vietoris y Walther Mayer siguieron desarrollando la teoría de los grupos algebraicos de homología en el período 1925-28.^[8]​^[9]​^[10]​ La nueva topología combinatoria trató formalmente las clases topológicas como grupo abelianos. Los grupos homológicos son grupos abelianos finitamente generados, y las clases homológicas son elementos de estos grupos. Los números de Betti de la variedad son el rango de la parte libre del grupo homológico, y los ciclos no orientables se describen mediante la parte de torsión.

La posterior difusión de los grupos de homología trajo un cambio de terminología y punto de vista de la "topología combinatoria" a la "topología algebraica".^[11]​ La homología algebraica sigue siendo el método principal para clasificar las variedades.^[12]​

Se define el n-ésimo grupo de homología asociado a un complejo de cadenas

${\displaystyle \ldots \to A_{n+1}{\stackrel {\delta _{n+1}}{\to }}A_{n}{\stackrel {\delta _{n}}{\to }}A_{n-1}\to \ldots }$

donde ${\displaystyle \delta _{n}\circ \delta _{n+1}=0}$

como el grupo abeliano

${\displaystyle H(A_{n})={\frac {\ker(\delta _{n})}{\rm {im(\delta _{n+1})}}}.}$

También se utiliza la notación

${\displaystyle H_{n}(A)}$, donde ${\displaystyle A}$ es el complejo de cadenas respectivo.

Se llama ${\displaystyle \ker(\delta _{n})}$ los ciclos en ${\displaystyle A_{n}}$ y se llama ${\displaystyle {\rm {im(\delta _{n+1})}}}$ las fronteras de ${\displaystyle A_{n}}$.

Se dice que la homología mide la falta de exactitud de un complejo de cadenas en cada uno de sus eslabones. Por ejemplo si tenemos un complejo de cadenas corto

${\displaystyle 0\to A_{1}{\stackrel {a_{1}}{\to }}A_{2}{\stackrel {a_{2}}{\to }}A_{3}\to 0}$

entonces sus correspondientes grup(os de homología son:

${\displaystyle H(A_{1})=\ker a_{1},\qquad H(A_{2})={\frac {{\rm {ker}}\ a_{2}}{{\rm {im}}\ a_{1}}},\qquad H(A_{3})={\frac {A_{3}}{{\rm {im}}\ a_{2}}}}$

Es obvio que si la sucesión fuese exacta, entonces estos grupos serían triviales (=0).

Los grupos de homotopía se parecen a los grupos de homología en que pueden representar "agujeros" en un espacio topológico. Existe una estrecha relación entre el primer grupo de homotopía ${\displaystyle \pi _{1}(X)}$ y el primer grupo de homología ${\displaystyle H_{1}(X)}$: el segundo es la abelianización del primero. De ahí que se diga que "la homología es una alternativa conmutativa a la homotopía".^[13]​^: 4:00 Los grupos de homotopía superiores son abelianos y están relacionados con los grupos de homología por el teorema de Hurewicz, pero pueden ser mucho más complicados. Por ejemplo, los grupos de homotopía de esferas no se comprenden bien y no se conocen en general, en contraste con la descripción directa dada anteriormente para los grupos de homología.

Como ejemplo, sea X la figura en ocho. Su primer grupo de homotopía ${\displaystyle \pi _{1}(X)}$ es el grupo de bucles dirigidos que empiezan y terminan en un punto predeterminado (por ejemplo, su centro). Es equivalente al grupo libre de rango 2, que no es conmutativo: hacer un bucle alrededor del ciclo más a la izquierda y luego alrededor del ciclo más a la derecha es diferente que hacer un bucle alrededor del ciclo más a la derecha y luego hacer un bucle alrededor del ciclo más a la izquierda. En cambio, su primer grupo de homología ${\displaystyle H_{1}(X)}$ es el grupo de cortes realizados en una superficie. Este grupo es conmutativo, ya que (informalmente) cortar el ciclo más a la izquierda y luego el ciclo más a la derecha conduce al mismo resultado que cortar el ciclo más a la derecha y luego el ciclo más a la izquierda.

• Álgebra homológica
• Cohomología
• Número de Betti
• Cohomología de De Rham
• Teoría de homología extraordinaria
• Álgebra homológica
• Grupo de homotopía
• Dualidad de Poincaré

• Hatcher, Allen (2002) Algebraic Topology Cambridge University Press
• Weisstein, Eric W. «Homology». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.