Interferometría , la enciclopedia libre

La interferometría es una familia de técnicas que consisten en combinar la luz (u otras ondas electromagnéticas) proveniente de diferentes receptores, telescopios o antenas de radio para obtener una imagen de mayor resolución aplicando el principio de superposición.^[1]​ Es utilizada en múltiples ciencias y tecnologías, como astronomía, climatología, fibra óptica, metrología, metrología óptica, oceanografía, sismología, espectroscopia (y sus aplicaciones a la química), mecánica cuántica, física nuclear y física de partículas, física del plasma, teledetección, interacciones biomoleculares, perfiles de superficie, microfluídica, tensión mecánica/medición de deformaciones, y velocimetría.^[2]​^: 1–2.

Esta técnica se utiliza especialmente en radioastronomía, siendo más difícil su implementación en longitudes de onda más corta (visible). La principal razón es la mayor precisión mecánica que se requiere al utilizar longitudes de onda más corta. En la actualidad hay proyectos ambiciosos de interferómetros ópticos de gran escala combinando los haces de luz de grandes telescopios terrestres, como el interferómetro Keck en Hawái y el Very Large Telescope Interferometer VLTI en Chile, mientras que entre los observatorios radioastronómicos se encuentran el Very Large Array (VLA) en EE. UU. y el Atacama Large Millimiter/submilliter Array (ALMA) en Chile.

En todos los casos el principio físico utilizado es que dos ondas de luz que coinciden en fase se amplifican mientras que dos ondas en oposición de fase se cancelan, existiendo también cualquier combinación intermedia. Esto permite mediante medición del grado de cancelación o amplificación de dos haces láser, realizar mediciones de superficies menores a la longitud de onda.

La interferometría no solo se utiliza en astronomía; existen usos más comunes como la medición de curvatura de lentes y espejos, así como la identificación de defectos tanto en su superficie como en su composición.

Para estas aplicaciones se pueden utilizar diferentes tipos de interferómetros, como el interferómetro Twyman-Green y el interferómetro de Fizeau, entre muchos otros.

Uno de los primeros usos de la interferometría fue en el famoso experimento de Michelson y Morley (1887), que demostró la inexistencia del éter, proporcionando las primeras evidencias experimentales en las que más tarde se asentaría la relatividad especial. En la actualidad, interferómetros similares al de Michelson se construyen en grandes instalaciones (véase LIGO o VIRGO) en un intento de detectar ondas gravitatorias, una consecuencia de la teoría de la relatividad general.

El 11 de febrero de 2016, investigadores del LIGO confirmaron la detección de ondas gravitacionales, observadas por primera vez en septiembre de 2015.

Los interferómetros y las técnicas interferométricas se pueden categorizar según los siguientes criterios:

W la detección homodina, la interferencia se produce entre dos haces con la misma longitud de onda (o frecuencia portadora). La diferencia de fase entre los dos haces provoca un cambio en la intensidad de la luz en el detector. Se mide la intensidad resultante de la luz tras la mezcla de estos dos haces, o se observa o registra el patrón de franjas de interferencia.^[3]​ La mayoría de los interferómetros discutidos en este artículo caen en esta categoría. La técnica heterodina se utiliza para (1) desplazar una señal de entrada a un nuevo rango de frecuencia y también (2) amplificar una señal de entrada débil (utilizando para ello un mezclador activo). Una señal de entrada débil de frecuencia f₁ es mezclada con una frecuencia de referencia fuerte f₂ de un oscilador local (OL). La combinación no lineal de las señales de entrada crea dos señales nuevas, una correspondiente a la suma de f₁ + f₂ de las dos frecuencias, y la otra es la diferencia f₁ − f₂. Estas frecuencias nuevas se denominan heterodinas. Por lo general se desea una de las nuevas frecuencias, y la otra señal es filtrada y descartada de la señal de salida. La señal de salida tendrá una intensidad proporcional al producto de las amplitudes de las señales de entrada.^[3]​

La aplicación más importante y utilizada de la técnica heterodina es en el receptor superheterodino (superhet), inventado en 1917-18 por el ingeniero estadounidense Edwin Howard Armstrong y el francés Lucien Lévy. En este circuito, la señal de radiofrecuencia entrante procedente de la antena se mezcla con una señal procedente de un oscilador local (LO) y se convierte mediante la técnica heterodina en una señal de frecuencia fija más baja denominada frecuencia intermedia (FI). Esta FI es amplificada y filtrada, antes de ser aplicada a un detector que extrae la señal de audio, que se envía al altavoz.^[4]​ La detección heterodina óptica es una extensión de la técnica heterodina a frecuencias más altas (visibles).^[3]​

Aunque la interferometría óptica heterodina suele realizarse en un único punto también es posible realizarla de campo amplio.^[5]​

Un interferómetro de doble trayectoria es aquel en el que el haz de referencia y el haz de muestra viajan por trayectorias divergentes. Algunos ejemplos son el interferómetro de Michelson, el interferómetro de Twyman-Green y el interferómetro de Mach-Zehnder. Después de ser perturbado por la interacción con la muestra bajo prueba, el haz de la muestra se recombina con el haz de referencia para crear un patrón de interferencia que puede ser interpretado.^[2]​^: 13–22

Un interferómetro de trayecto común es una clase de interferómetro en el que el haz de referencia y el haz de la muestra viajan por el mismo camino. La Fig. 4 ilustra el interferómetro de Sagnac, el giroscopio de fibra óptica, el interferómetro de difracción puntual y el interferómetro de cizallamiento lateral. Otros ejemplos de interferómetro de trayecto común son el microscopio de contraste de fase de Zernike, el Biprisma de Fresnel, el Sagnac de área cero y el interferómetro de placa de dispersión.^[6]​

Un interferómetro de división de frente de onda divide un frente de onda de luz que emerge de un punto o de una rendija estrecha (es decir luz espacialmente coherente) y, después de permitir que las dos partes del frente de onda viajen por caminos diferentes, permite que se recombinen.^[7]​ La Fig. 5 ilustra el experimento de interferencia de Young y el espejo de Lloyd. Otros ejemplos de interferómetro de división del frente de onda son el biprisma de Fresnel, el Billet Bi-Lens y el interferómetro de Rayleigh.^[8]​

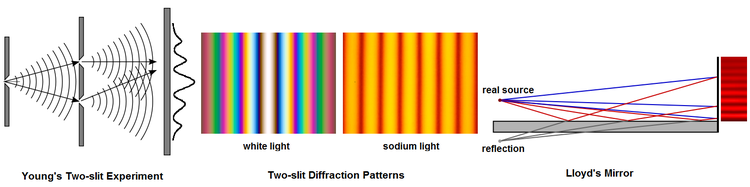
En 1803, el experimento de interferencia de Young jugó un papel importante en la aceptación general de la teoría ondulatoria de la luz. Si se utiliza luz blanca en el experimento de Young, el resultado es una banda central blanca de interferencia constructiva que corresponde a una longitud de trayectoria igual desde las dos rendijas, rodeada por un patrón simétrico de franjas de color de intensidad decreciente. Además de la radiación electromagnética continua, el experimento de Young se ha realizado con fotones individuales,^[9]​ con electrones,^[10]​^[11]​ y con moléculas buckyball lo suficientemente grandes como para ser vistas con un microscopio electrónico.^[12]​

El espejo de Lloyd genera franjas de interferencia combinando la luz directa de una fuente (líneas azules) y la luz de la imagen reflejada de la fuente (líneas rojas) de un espejo mantenido en incidencia rasante. El resultado es un patrón asimétrico de franjas. La banda de igual longitud de trayectoria, más cercana al espejo, es más oscura que brillante. En 1834, Humphrey Lloyd interpretó este efecto como una prueba de que la fase de un rayo reflejado en la superficie frontal se invierte.^[13]​^[14]​

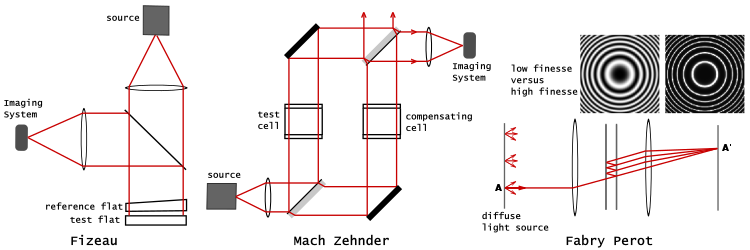
Un interferómetro de división de amplitud utiliza un reflector parcial para dividir la amplitud de la onda incidente en haces separados que se separan y recombinan.

El interferómetro de Fizeau se muestra tal y como se podría montar para probar un plano óptico. Se coloca un plano de referencia exactamente calculado sobre el plano que se está probando, separado por estrechos espaciadores. El plano de referencia está ligeramente biselado (sólo es necesaria una fracción de grado de biselado) para evitar que la superficie posterior del plano produzca franjas de interferencia. La separación de los planos de prueba y de referencia permite inclinar los dos planos entre sí. Ajustando la inclinación, que añade un gradiente de fase controlado al patrón de franjas, se puede controlar el espaciado y la dirección de las franjas, de modo que se puede obtener una serie de franjas casi paralelas fácil de interpretar en lugar de un complejo remolino de líneas de contorno. Sin embargo, para separar las placas es necesario colimar la luz que las ilumina. La Fig 6 muestra un haz colimado de luz monocromática que ilumina las dos placas y un divisor de haz que permite ver las franjas en el eje.^[15]​^[16]​

El interferómetro de Mach-Zehnder es un instrumento más versátil que el interferómetro de Michelson. Cada una de las trayectorias de luz bien separadas se recorre sólo una vez, y las franjas pueden ajustarse de manera que se localicen en cualquier plano deseado.^[2]​^: 18 Normalmente, las franjas se ajustan para que se sitúen en el mismo plano que el objeto de prueba, de modo que las franjas y el objeto de prueba puedan fotografiarse juntos. Si se decide producir franjas con luz blanca, entonces, dado que la luz blanca tiene una longitud de coherencia limitada, del orden de micrómetro, hay que tener mucho cuidado para igualar los caminos ópticos o no se verán las franjas. Como se ilustra en la Fig. 6, se colocaría una célula de compensación en la trayectoria del haz de referencia para igualar la célula de prueba. Observe también la orientación precisa de los divisores de haz. Las superficies reflectantes de los divisores de haz se orientarían de forma que los haces de prueba y de referencia atravesaran una cantidad igual de vidrio. En esta orientación, los haces de prueba y de referencia experimentan cada uno dos reflexiones en la superficie frontal, lo que resulta en el mismo número de inversiones de fase. El resultado es que la luz que recorre un camino óptico igual en los haces de prueba y de referencia produce una franja de luz blanca de interferencia constructiva.^[17]​^[18]​

El corazón del interferómetro Fabry-Pérot es un par de planos ópticos de vidrio parcialmente plateados, separados por varios milímetros o centímetros, con las superficies plateadas enfrentadas. (Como alternativa, un etalón de Fabry-Pérot utiliza una placa transparente con dos superficies reflectantes paralelas.)^[2]​^: 35–36 Al igual que en el interferómetro de Fizeau, las planchas están ligeramente biseladas. En un sistema típico, la iluminación es proporcionada por una fuente difusa colocada en el plano focal de una lente colimadora. Una lente de enfoque produce lo que sería una imagen invertida de la fuente si los planos emparejados no estuvieran presentes, es decir, en ausencia de los planos emparejados, toda la luz emitida desde el punto A que pasa por el sistema óptico se enfocaría en el punto A'. En la Fig. 6, sólo se traza un rayo emitido desde el punto A de la fuente. A medida que el rayo pasa a través de los planos emparejados, se refleja de forma múltiple para producir múltiples rayos transmitidos que son recogidos por la lente de enfoque y llevados al punto A' en la pantalla. El patrón de interferencia completo toma la apariencia de un conjunto de anillos concéntricos. La nitidez de los anillos depende de la reflectividad de los planos. Si la reflectividad es alta, dando lugar a un factor Q alto (es decir alta fineza), la luz monocromática produce un conjunto de anillos estrechos y brillantes contra un fondo oscuro.^[19]​ En la Fig. 6, la imagen de baja finura corresponde a una reflectividad de 0,04 (es decir, superficies sin depurar) frente a una reflectividad de 0,95 para la imagen de alta finura.

La Fig. 6 ilustra los interferómetros Fizeau, Mach-Zehnder y Fabry-Pérot. Otros ejemplos de interferómetros de división de amplitud son el Michelson, el Twyman-Green, el interferómetro de trayectoria desigual del láser y el interferómetro de Linnik.^[20]​

Michelson y Morley (1887)^[21]​ y otros de los primeros experimentadores que utilizaban técnicas interferométricas en un intento de medir las propiedades del éter luminífero, utilizaban luz monocromática sólo para la configuración inicial de sus equipos, cambiando siempre a luz blanca para las mediciones reales. La razón es que las mediciones se registraban visualmente. La luz monocromática daría lugar a un patrón de franjas uniforme. A falta de medios modernos de control de la temperatura ambiental, los experimentadores se enfrentaban a la deriva continua de las franjas, aunque el interferómetro se instalara en un sótano. Dado que las franjas desaparecían ocasionalmente debido a las vibraciones del tráfico de caballos, las tormentas eléctricas lejanas y similares, era fácil que un observador se "perdiera" cuando las franjas volvían a ser visibles. Las ventajas de la luz blanca, que producía un patrón de franjas de color distintivo, superaban con creces las dificultades de alinear el aparato debido a su baja longitud de coherencia.^[22]​ Este fue un ejemplo temprano del uso de la luz blanca para resolver la "ambigüedad de 2 pi".

• Luz coherente
• Interferómetro de trayecto común
• Interferómetro de Fizeau
• Interferómetro de Michelson
• Interferómetro Fabry-Pérot
• Interferómetro de Mach-Zehnder
• Síntesis de apertura
• Interferencia
• Tomografía de coherencia óptica
• Interferometría de muy larga base
• Principio de superposición

• Wikimedia Commons alberga una categoría multimedia sobre Interferometría.