Modelo Lambda-CDM , la enciclopedia libre

Cosmología física
Big Bang y evolución del universo
Artículos
Universo primitivo	Teoría del Big Bang Inflación cósmica Bariogénesis Nucleosíntesis primordial Creacionismo
Expansión	Expansión métrica del espacio Expansión acelerada del universo Ley de Hubble Corrimiento al rojo
Estructura	Forma del universo Espacio-tiempo Materia bariónica Universo Materia oscura Energía oscura
Experimentos	Planck (satélite) WMAP COBE
Científicos	Albert Einstein Edwin Hubble Georges Lemaître Stephen Hawking George Gamow Mustapha Ishak-Boushaki
Portales
Principal	Cosmología
Otros	Física Astronomía Exploración espacial Sistema Solar
[editar datos en Wikidata]

En cosmología, el modelo Lambda-CDM o ΛCDM (del inglés: Lambda-Cold Dark Matter) representa el modelo de concordancia del Big Bang que explica las observaciones cósmicas de la radiación de fondo de microondas, así como la estructura a gran escala del universo y las observaciones realizadas de supernovas, arrojando luz sobre la explicación de la aceleración de la expansión del Universo. Es el modelo conocido más simple que está de acuerdo con todas las observaciones.

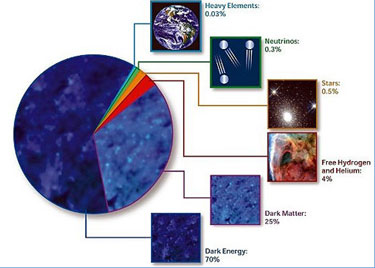
• Λ (lambda) indica la constante cosmológica como parte de un término de la energía oscura que permite conocer el valor actual de la expansión acelerada del Universo que se inició hace unos 6 mil millones de años.^[1]​ La constante cosmológica se describe en términos de ${\displaystyle \Omega _{\Lambda }}$, la fracción de densidad de energía de un universo plano. En la actualidad, ${\displaystyle \Omega _{\Lambda }\simeq }$ 0.70, lo que implica que equivale al 70% de la densidad de energía del presente universo.
• La materia oscura fría es el modelo de materia oscura en el que la velocidad de sus partículas es muy inferior a la velocidad de la luz, de ahí el adjetivo "fría". La materia oscura fría es no-bariónica, a diferencia de la materia bariónica normal con la que no interacciona excepto mediante la gravedad. Este componente constituye el 26% de la densidad de la energía del actual universo. El 4% restante es toda la materia y energía (materia bariónica), que componen los átomos y los fotones que son los bloques que construyen los planetas, las estrellas y las nubes de gas en el universo.
• El modelo supone un espectro de casi invariancia de escala de perturbaciones primordiales y un universo sin curvatura espacial. También asume que no tiene ninguna topología observable, de modo que el universo es mucho más grande que el horizonte observable de la partícula. Se dan predicciones de inflación cósmica.

El modelo asume que la Relatividad General es la teoría correcta de la gravedad a escalas cosmológicas. Es frecuentemente nombrado como el modelo estándar de la cosmología del Big Bang, porque es el modelo más simple que proporciona una explicación razonablemente buena de las siguientes propiedades del cosmos:

• La existencia y estructura del fondo cósmico de microondas
• La estructura a gran escala de la distribución de galaxias
• Las abundancias de hidrógeno (incluyendo deuterio), helio y litio
• La expansión acelerada del universo observado en distantes galaxias y supernovas

El modelo ΛCDM se ha simulado con éxito en superordenadores: partiendo de la composición que tenía el Universo (átomos de hidrógeno, helio, litio, etc, fotones, neutrinos,… transcurridos 11.5 millones de años después del Big-Bang, la simulación forma estrellas, galaxias y estructuras de cúmulos y supercúmulos de galaxias muy similares a los objetos reales que observamos en el firmamento^[2]​ El modelo ΛCDM se puede ampliar añadiendo la inflación cosmológica, la quintaesencia y otros elementos que son áreas actuales de estudio e investigación en Cosmología.

El descubrimiento en 1965 del fondo cósmico de microondas (Cosmic Microwave Background , o CMB) confirmó una predicción clave de la cosmología del Big Bang. A partir de ahí, se aceptó generalmente que el universo empezó en un estado denso y caliente y que se ha ido expandiendo con el tiempo. La tasa de expansión depende de los tipos de materia y energía presentes en el universo, y, en particular, de si la densidad total está por encima o por debajo de la llamada densidad crítica. Durante la década de 1970, la atención se centró en los modelos bariónicos puros, pero tenían graves problemas para explicar la formación de las galaxias dadas las pequeñas anisotropías observadas en el CMB (límites superiores en ese momento). A principios de 1980, se pensó que esto se podría resolver si la materia oscura fría dominase sobre los bariones, y la teoría de la inflación cósmica motivó modelos con densidad crítica. Durante la década de 1980, la mayoría de las investigaciones se centraron en la materia oscura fría con densidad crítica en materia, en torno al 95% de CDM y el 5% de bariones: éstos mostraron con éxito la formación de galaxias y de los cúmulos de galaxias, pero seguían teniendo problemas; en particular, el modelo requería una constante de Hubble menor que la preferida por las observaciones y el modelo hacía bajas predicciones sobre los agrupamiento de galaxias a gran escala. Estas dificultades aumentaron con el descubrimiento en 1992 de la anisotropía del CMB observada por el COBE, y comenzaron a considerarse varias alternativas incluyendo la ΛCDM y otros modelos de materia oscura mezcla fría+caliente. El modelo ΛCDM se convirtió entonces en el estándar siguiendo las observaciones en 1998 de la expansión acelerada del Universo, y fue respaldado rápidamente por otras observaciones: en 2000, el experimento de fondo de microondas BOOMERanG midió la densidad total (materia+energía) que estaba cerca del 100% de la crítica, mientras que en 2001 la exploración de galaxias en el infrarrojo 2dFGRS midió la densidad de materia que era de cerca de 25%; la gran diferencia entre ambas apoya una Λ positiva o energía oscura. Las mediciones del fondo de microondas mucho más precisas hechas por el WMAP en 2003-2010 han seguido apoyando y refinando el modelo.

Hay en la actualidad investigaciones activas de muchos aspectos del modelo ΛCDM, tanto para refinar sus parámetros como para detectar posiblemente desviaciones. Además, el ΛCDM no tiene ninguna teoría física explícita que explique el origen o la naturaleza física de la materia oscura o energía oscura; el casi invariante espectro de perturbaciones del CMB, y su imagen a través de la esfera celeste, se cree que son el resultado de irregularidades térmicas y acústicas muy pequeñas en el punto de recombinación. Una gran mayoría de astrónomos y astrofísicos apoyan el modelo ΛCDM u otros próximos, pero Milgrom, McGaugh y Kroupa encabezan otras posiciones críticas, atacando las porciones de materia oscura de la teoría desde la perspectiva de los modelos de formación de galaxias y apoyando la teoría alternativa MOND, que requiere una modificación de las ecuaciones de Einstein y de las ecuaciones de Friedmann como se ve en algunas propuestas, como la teoría de MOG o teoría TeVeS (Tensor–vector–scalar gravity). Otras propuestas de astrofísicos teóricos o alternativas cosmológicas a la relatividad general de Einstein que tratan de explicar la energía oscura o la materia oscura son la gravedad f (R), la teoría tensort-escalar, la cosmología de branas, el modelo de DGP y teorías galileon.

Las búsquedas exhaustivas de partículas de materia oscura hasta ahora no han demostrado una detección adecuada. La energía oscura puede ser casi imposible de detectar en un laboratorio. La comparación del modelo con las observaciones es viable a escalas grandes, pero puede tener problemas en las escalas pequeñas, prediciendo muchas galaxias enanas y gran cantidad materia oscura en las regiones más internas del espacio. Trabajando en pequeñas escalas es más difícil encontrar soluciones usando simulaciones por computadora, por lo que aún no está claro si el problema son las simulaciones, las propiedades no estándar de la materia oscura o un error en el modelo.^[3]​

El modelo tiene seis parámetros. El parámetro de Hubble determina el índice de la expansión del universo, así como la densidad crítica para el encierro del universo, ${\displaystyle \scriptstyle \rho _{0}}$. Las densidades para los bariones, la materia oscura y la energía oscura se dan como ${\displaystyle \scriptstyle \rho _{0}}$, que son el cociente de la densidad verdadera a la densidad crítica: por ejemplo ${\displaystyle \scriptstyle \Omega _{b}=\rho _{b}/\rho _{0}}$. Puesto que el modelo de ΛCDM supone un universo plano, la suma de estas densidades a una, y la densidad de la energía oscura no es un parámetro libre. La profundidad óptica al reionizar determina el desplazamiento al rojo de la emisión por reionización. La información sobre las fluctuaciones de la densidad es determinada por la amplitud de las fluctuaciones primordiales (de la inflación cósmica) y del índice espectral, que mide cómo las fluctuaciones cambian con la escala (el ns = 1 corresponde a un espectro escalar-invariante).

Los errores cotizados son 1σ: es decir, existe una probabilidad del 68% que el valor verdadero baja dentro de los límites superiores y más bajos del error. Los errores no son gaussianos, y han sido derivados usando un análisis de cadenas de Markov Monte Carlo (MCMC) por la colaboración de Wilkinson Microwave Anisotropy Probe (Spergel et al. 2006) que también utiliza los datos de la supernova de Sloan Digital Sky Survey y de la supernova de tipo Ia.

Parámetro	Valor	Descripción
Parámetros básicos
H0	${\displaystyle 73.2_{-3.2}^{+2.4}}$ km s-1 Mpc-1	parámetro de Hubble
Ωb	${\displaystyle 0.0444_{-0.0035}^{+0.0042}}$	Densidad bariónica
Ωm	${\displaystyle 0.266_{-0.040}^{+0.025}}$	Densidad total de materia (bariones + materia oscura)
τ	${\displaystyle 0.079_{-0.032}^{+0.029}}$	camino óptico hasta la reionización
As	${\displaystyle 0.813_{-0.052}^{+0.042}}$	Amplitud de fluctuación escalar
ns	${\displaystyle 0.948_{-0.018}^{+0.015}}$	Índice espectral escalar
Parámetros Derivados
ρ0	${\displaystyle 0.94_{-0.09}^{+0.06}\times 10^{-26}}$ kg/m³	Densidad crítica
ΩΛ	${\displaystyle 0.732_{-0.025}^{+0.040}}$	Densidad de energía oscura
zion	${\displaystyle 10.5_{-2.9}^{+2.6}}$	Desplazamiento al rojo de la reionización
σ8	${\displaystyle 0.772_{-0.048}^{+0.036}}$	Amplitud de fluctuación de galaxias
t0	${\displaystyle 13.73_{-0.17}^{+0.13}\times 10^{9}}$ años	Edad del universo

Massimo Persic y Paolo Salucci estimaron por primera vez la densidad bariónica presente hoy en los grupos de galaxias elípticas y espirales. Realizaron una integración de la relación bariónica de masa a luz sobre la luminosidad, ponderada con la función de luminosidad (en ${\displaystyle M_{b}/L}$) sobre los tipos de objetos mencionados:

${\displaystyle \rho _{b}=\sum \int L\phi (L){\frac {M_{b}}{L}}\,dL.}$

El resultado fue:

${\displaystyle \Omega _{b}=\Omega _{*}+\Omega _{\text{gas}}=2.2\times 10^{-3}+1.5\times 10^{-3}h^{-1.3}\simeq 0.003}$

donde ${\displaystyle h\simeq 0.72}$.

El valor es mucho más bajo que la predicción de ${\displaystyle \Omega _{b}\simeq 0.048}$ de nucleosíntesis cósmica estándar, por lo que las estrellas y el gas en grupos de galaxias representan menos del 10% de los bariones que son sintetizados. Este problema se conoce como el problema de los «bariones perdidos».^[4]​

Las extensiones posibles del modelo más simple de ΛCDM permiten la quintaesencia haciendo que sea más bien una constante cosmológica. En este caso, la ecuación de estado de la energía oscura es diferente de −1. La inflación cósmica predice las fluctuaciones del tensor (ondas gravitacionales). Su amplitud es dada por parámetros como el cociente tensor-a-escalar, que es determinado por la escala de la energía de la inflación. Otras modificaciones permiten curvatura espacial o un índice espectral corriente, que se ven generalmente como contrarias con la inflación cósmica. Permitir estos parámetros en la teoría aumentará generalmente los errores en los parámetros tabulados arriba, y puede también cambiar la posición de los valores observados.

Parámetro	Valor	Descripción
w	${\displaystyle -0.926_{-0.075}^{+0.051}}$	Ecuación de estado
r	${\displaystyle <0.55}$ (2σ)	Ratio Tensor-a-escalar
Ωk	${\displaystyle -0.010_{-0.012}^{+0.014}}$	Curvatura espacial
α	${\displaystyle -0.102_{-0.043}^{+0.050}}$	Índice espectral
${\displaystyle \Sigma m_{\nu }}$	${\displaystyle <0.87}$ eV (2σ)	Suma total de las masas de los neutrinos

Estos valores son consistentes con una constante cosmológica, un valor W = 1, y ninguna curvatura espacial ${\displaystyle \Omega _{k}=0}$. Hay una cierta evidencia para un índice espectral corriente, pero no es estadísticamente significativo. Las expectativas teóricas sugieren que el cociente tensor-a-escalar r esté entre 0 y 0.3, y así que se deben probar este valor en un futuro próximo.

• D. N. Spergel et al. (WMAP collaboration) (marzo de 2006). Wilkinson Microwave Anisotropy Probe (WMAP) three year results: implications for cosmology. 
• M. Tegmark et al. (SDSS collaboration), Cosmological Parameters from SDSS and WMAP, Phys. Rev. D69 103501 (2004).
• D. N. Spergel et al. (WMAP collaboration), First year Wilkinson Microwave Anisotropy Probe (WMAP) observations: determination of cosmological parameters, Astrophys. J. Suppl. 148 175 (2003).
• R. Rebolo et al. (VSA collaboration), Cosmological parameter estimation using Very Small Array data out to l=1500, Monthly Notices of the Royal Astronomical Society, Volume 353, Issue 3, pp. 747-759
• J. P. Ostriker and P. J. Steinhardt, Cosmic Concordance, arXiv:astro-ph/9505066.