Número poligonal , la enciclopedia libre
 |
 |
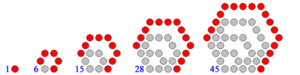 |
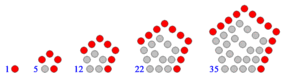
| Los cuatro primeros tipos de números poligonales: números triangulares, cuadrangulares, pentagonales y hexagonales |
En matemáticas, un número poligonal es un número natural que puede recomponerse en un polígono regular. Los matemáticos de la Antigüedad descubrieron que los números podían disponerse con ciertas formas cuando los representaban mediante piedras o semillas.
Números poligonales
[editar]El número 10 puede recomponerse como un triángulo (véase número triangular):
Sin embargo, el 10 no puede formar un cuadrado, pero el 9 sí (véase número cuadrado):
Algunos números, como el 36, pueden recomponerse tanto en un cuadrado como en un triángulo (véase número cuadrado triangular):
El método empleado para agrandar el polígono hasta el siguiente tamaño es extender dos brazos adyacentes por un punto y luego añadir los lados extra requeridos entre los puntos.
Fórmulas
[editar]
Si s es el número de lados de un polígono, la fórmula para el n-ésimo número s-gonal P(s,n) es
o
El n-ésimo número s-gonal también está relacionado con los números triangulares Tn de la siguiente manera:
Por lo tanto:
Para un número s-gonal dado P(s,n) = x, se puede encontrar n mediante la fórmula
y a su vez se puede encontrar s calculando
- .
Cada número hexagonal es también un número triangular
[editar]Aplicando la fórmula anterior:
al caso de 6 lados, se obtiene:
pero sabiendo que:
resulta:
Esto demuestra que el n-'esimo número hexagonal P(6,n) es también el (2n − 1)-ésimo número triangular T2n−1. Se puede determinar la secuencia de los números hexagonales simplemente tomando los números triangulares impares:
- 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, ...
n-ésimo número poligonal
[editar]Si es el número de lados de un polígono, entonces la fórmula para el -ésimo número poligonal de lados es .
Propiedades
[editar]La siguiente tabla incluye algunas propiedades de las series definidas por los números poligonales. Son especialmente relevantes los resultados de la suma de los inversos de los números poligonales . Los primeros 6 valores en la columna "suma de inversos", para números triangulares a octagonales, provienen de una solución publicada al problema general, que también da una fórmula general para cualquier número de lados, en términos de la función digamma.[1]
El OEIS evita los términos que usan prefijos griegos (por ejemplo, "octagonal") en favor de términos que usan números (es decir, "8-gonal").
Una propiedad de esta tabla se puede expresar mediante la siguiente identidad (consúltese A086270):
con
| s | Nombre | Fórmula | Suma de los inversos[2][3] | n | número OEIS | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |||||
| 3 | Triangular | 12(n2 + n) | 2[[2]] | 1 | 3 | 6 | 10 | 15 | 21 | 28 | 36 | 45 | 55 | 66 | 78 | 91 | A000217 |
| 4 | Cuadrado | 12(2n2 - 0n) = n2 | π26[[2]] | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | A000290 |
| 5 | Pentagonal | 12(3n2 - n) | 3 ln 3 - π√33[[2]] | 1 | 5 | 12 | 22 | 35 | 51 | 70 | 92 | 117 | 145 | 176 | 210 | 247 | A000326 |
| 6 | Hexagonal | 12(4n2 - 2n) = 2n2 - n | 2 ln 2[[2]] | 1 | 6 | 15 | 28 | 45 | 66 | 91 | 120 | 153 | 190 | 231 | 276 | 325 | A000384 |
| 7 | Heptagonal | 12(5n2 - 3n) | [[2]] | 1 | 7 | 18 | 34 | 55 | 81 | 112 | 148 | 189 | 235 | 286 | 342 | 403 | A000566 |
| 8 | Octagonal | 12(6n2 - 4n) = 3n2 - 2n | 34 ln 3 + π√312[[2]] | 1 | 8 | 21 | 40 | 65 | 96 | 133 | 176 | 225 | 280 | 341 | 408 | 481 | A000567 |
| 9 | Nonagonal | 12(7n2 - 5n) | 1 | 9 | 24 | 46 | 75 | 111 | 154 | 204 | 261 | 325 | 396 | 474 | 559 | A001106 | |
| 10 | Decagonal | 12(8n2 - 6n) = 4n2 - 3n | ln 2 + π6 | 1 | 10 | 27 | 52 | 85 | 126 | 175 | 232 | 297 | 370 | 451 | 540 | 637 | A001107 |
| 11 | Hendecagonal | 12(9n2 - 7n) | 1 | 11 | 30 | 58 | 95 | 141 | 196 | 260 | 333 | 415 | 506 | 606 | 715 | A051682 | |
| 12 | Dodecagonal | 12(10n2 - 8n) | 1 | 12 | 33 | 64 | 105 | 156 | 217 | 288 | 369 | 460 | 561 | 672 | 793 | A051624 | |
| 13 | Tridecagonal | 12(11n2 - 9n) | 1 | 13 | 36 | 70 | 115 | 171 | 238 | 316 | 405 | 505 | 616 | 738 | 871 | A051865 | |
| 14 | Tetradecagonal | 12(12n2 - 10n) | 25 ln 2 + 310 ln 3 + π√310 | 1 | 14 | 39 | 76 | 125 | 186 | 259 | 344 | 441 | 550 | 671 | 804 | 949 | A051866 |
| 15 | Pentadecagonal | 12(13n2 - 11n) | 1 | 15 | 42 | 82 | 135 | 201 | 280 | 372 | 477 | 595 | 726 | 870 | 1027 | A051867 | |
| 16 | Hexadecagonal | 12(14n2 - 12n) | 1 | 16 | 45 | 88 | 145 | 216 | 301 | 400 | 513 | 640 | 781 | 936 | 1105 | A051868 | |
| 17 | Heptadecagonal | 12(15n2 - 13n) | 1 | 17 | 48 | 94 | 155 | 231 | 322 | 428 | 549 | 685 | 836 | 1002 | 1183 | A051869 | |
| 18 | Octadecagonal | 12(16n2 - 14n) | 47 ln 2 - √214 ln (3 - 2√2) + π(1 + √2)14 | 1 | 18 | 51 | 100 | 165 | 246 | 343 | 456 | 585 | 730 | 891 | 1068 | 1261 | A051870 |
| 19 | Eneadecagonal | 12(17n2 - 15n) | 1 | 19 | 54 | 106 | 175 | 261 | 364 | 484 | 621 | 775 | 946 | 1134 | 1339 | A051871 | |
| 20 | Icosagonal | 12(18n2 - 16n) | 1 | 20 | 57 | 112 | 185 | 276 | 385 | 512 | 657 | 820 | 1001 | 1200 | 1417 | A051872 | |
| 21 | Icosihenagonal | 12(19n2 - 17n) | 1 | 21 | 60 | 118 | 195 | 291 | 406 | 540 | 693 | 865 | 1056 | 1266 | 1495 | A051873 | |
| 22 | Icosidigonal | 12(20n2 - 18n) | 1 | 22 | 63 | 124 | 205 | 306 | 427 | 568 | 729 | 910 | 1111 | 1332 | 1573 | A051874 | |
| 23 | Icositrigonal | 12(21n2 - 19n) | 1 | 23 | 66 | 130 | 215 | 321 | 448 | 596 | 765 | 955 | 1166 | 1398 | 1651 | A051875 | |
| 24 | Icositetragonal | 12(22n2 - 20n) | 1 | 24 | 69 | 136 | 225 | 336 | 469 | 624 | 801 | 1000 | 1221 | 1464 | 1729 | A051876 | |
| 25 | Icosipentagonal | 12(23n2 - 21n) | 1 | 25 | 72 | 142 | 235 | 351 | 491 | 652 | 837 | 1045 | 1276 | 1530 | 1807 | A051877 | |
| 26 | Icosihexagonal | 12(24n2 - 22n) | 1 | 26 | 75 | 148 | 245 | 366 | 511 | 680 | 873 | 1090 | 1331 | 1596 | 1885 | A051878 | |
| 27 | Icosiheptagonal | 12(25n2 - 23n) | 1 | 27 | 78 | 154 | 255 | 381 | 532 | 708 | 909 | 1135 | 1386 | 1662 | 1963 | A051879 | |
| 28 | Icosioctagonal | 12(26n2 - 24n) | 1 | 28 | 81 | 160 | 265 | 396 | 553 | 736 | 945 | 1180 | 1441 | 1728 | 2041 | A051880 | |
| 29 | Icosienagonal | 12(27n2 - 25n) | 1 | 29 | 84 | 166 | 275 | 411 | 574 | 764 | 981 | 1225 | 1496 | 1794 | 2119 | A051881 | |
| 30 | Triacontagonal | 12(28n2 - 26n) | 1 | 30 | 87 | 172 | 285 | 426 | 595 | 792 | 1017 | 1270 | 1551 | 1860 | 2197 | A051882 | |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 10000 | Miriagonal | 12(9998n2 - 9996n) | A167149 | ||||||||||||||
Números multipoligonales
[editar]Algunos números, como el 36, que es tanto cuadrado como triangular, pertenece a dos conjuntos de números poligonales. El problema de determinar, dados dos conjuntos de este tipo, todos los números que pertenecen a ambos se puede resolver reduciendo el problema a una ecuación de Pell. El ejemplo más simple es la secuencia de números cuadrados triangulares.
La siguiente tabla resume el conjunto de números s-gonales t-gonales para valores pequeños de s y t.
s t Secuencia Número OEIS 4 3 1, 36, 1225, 41616, 1413721, 48024900, 1631432881, 55420693056, 1882672131025, 63955431761796, 2172602007770041, 73804512832419600, 2507180834294496361, 85170343853180456676, 2893284510173841030625, 98286503002057414584576, 3338847817559778254844961, ... A001110 5 3 1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465, … A014979 5 4 1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801, ... A036353 6 3 Todos los números hexagonales también son triangulares. A000384 6 4 1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625, 3338847817559778254844961, 3853027488179473932250054441, ... A046177 6 5 1, 40755, 1533776805, … A046180 7 3 1, 55, 121771, 5720653, 12625478965, 593128762435, 1309034909945503, 61496776341083161, 135723357520344181225, 6376108764003055554511, 14072069153115290487843091, … A046194 7 4 1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449, 9976444135331412025, … A036354 7 5 1, 4347, 16701685, 64167869935, … A048900 7 6 1, 121771, 12625478965, … A048903 8 3 1, 21, 11781, 203841, … A046183 8 4 1, 225, 43681, 8473921, 1643897025, 318907548961, 61866420601441, 12001766689130625, 2328280871270739841, 451674487259834398561, 87622522247536602581025, 16998317641534841066320321, … A036428 8 5 1, 176, 1575425, 234631320, … A046189 8 6 1, 11781, 113123361, … A046192 8 7 1, 297045, 69010153345, … A048906 9 3 1, 325, 82621, 20985481, … A048909 9 4 1, 9, 1089, 8281, 978121, 7436529, 878351769, 6677994961, 788758910641, 5996832038649, 708304623404049, 5385148492712041, 636056763057925561, ... A036411 9 5 1, 651, 180868051, … A048915 9 6 1, 325, 5330229625, … A048918 9 7 1, 26884, 542041975, … A048921 9 8 1, 631125, 286703855361, … A048924
En algunos casos, como s = 10 y t = 4, no hay números en ambos conjuntos distintos del 1.
El problema de encontrar números que pertenezcan a tres conjuntos poligonales es más difícil. Una búsqueda por computadora de números triangulares cuadrados pentagonales ha arrojado solo el valor trivial de 1, aunque aún no se ha encontrado una prueba de que no exista algún número que pueda pertenecer a las tres clases.[4]
El número 1225 es hecatonicositetragonal (s = 124), hexacontagonal (s = 60), icosienneagonal (s = 29), hexagonal, cuadrado y triangular.
El único conjunto poligonal que está contenido completamente en otro conjunto poligonal es el conjunto de números hexagonales, que está contenido en el conjunto de números triangulares.[cita requerida]
Véase también
[editar]Referencias
[editar]- ↑ «Archived copy». Archivado desde el original el 15 de junio de 2011. Consultado el 13 de junio de 2010.
- ↑ a b c d e f g «Archived copy». Archivado desde el original el 15 de junio de 2011. Consultado el 13 de junio de 2010.
- ↑ «Beyond the Basel Problem: Sums of Reciprocals of Figurate Numbers». Archivado desde el original el 29 de mayo de 2013. Consultado el 6 de marzo de 2021.
- ↑ Weisstein, Eric W. «Pentagonal Square Triangular Number». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
Bibliografía
[editar]- The Penguin Dictionary of Curious and Interesting Numbers, David Wells (Penguin Books, 1997) [ISBN 0-14-026149-4] (en inglés).
- Weisstein, Eric W. «Polygonal numbers». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.


 French
French Deutsch
Deutsch
















