Onda triangular , la enciclopedia libre

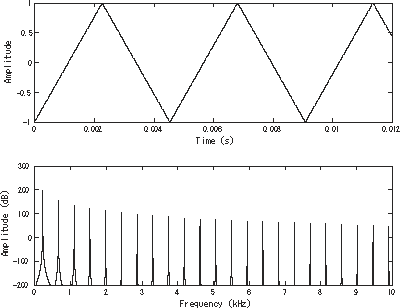
La onda triangular es un tipo de señal periódica que presenta unas velocidades de subida y bajada (Slew Rate) constantes. Lo más habitual es que sea simétrica, es decir que, los tiempos de subida y bajada son iguales.

La onda triangular tiene un contenido en armónicos muy bajo, lo que concuerda con su parecido a una onda senoidal. Tanto matemática como físicamente se puede obtener integrando en el tiempo una onda cuadrada: los niveles constantes alto y bajo de dicha onda se convierten en las pendientes (constantes) de los flancos de subida y bajada de la onda triangular.

Es posible aproximar la señal onda triangular con síntesis aditiva sumando los armónicos impares de la fundamental mientras se multiplican cada otros armónicos singulares por -1 (o, equivalente, cambiando su fase por π) y multiplicando la amplitud de los armónicos por uno sobre la raíz de su número modal , n, (la cual es equivalente a unos sobre el cuadrado de su frecuencia relativa a la fundamental).

Lo arriba expuesto puede ser descrito matemáticamente como lo siguiente:

${\displaystyle {\begin{aligned}x_{\mathrm {triangle} }(t)&{}=\sum _{i=0}^{N}(-1)^{i}n^{-2}\left(\sin[nt]\right)\end{aligned}}}$

Donde N es el número de armónicos que se incluyen en la aproximación, t es la variable independiente (p.e. tiempo para ondas sonoras), y i es la etiqueta armónica que está relacionada con el número modal por ${\displaystyle n=2i+1}$.

Esta infinita Serie de Fourier converge en la señal onda triangular como N que tiende a infinito.

Las ondas triangulares tienen aplicaciones destacadas, tales como:

• Generación de señales sinusoidales. Se generan ondas sinusoidales conformando la señal triangular con redes de resistencias y diodos. Es el método habitual para producir sinusoides en los generadores de funciones de baja frecuencia (hasta unos 10 MHz).
• Generación de barridos. En los tubos de rayos catódicos, se aplican tensiones triangulares asimétricas (diente de sierra) a las placas deflectoras, en el caso de osciloscopios, o corrientes de la misma forma a las bobinas deflectoras, en el caso de monitores de televisión, pantallas de ordenador, etc.
• Osciladores. Como la relación entre el tiempo y la amplitud de una onda triangular es lineal, resulta conveniente para realizar osciladores controlados por tensión, comparando su nivel con la tensión de control.

• Onda cuadrada
• Oscilador

• Wikimedia Commons alberga una categoría multimedia sobre Onda triangular.