Pirámide pentagonal , la enciclopedia libre
| Pirámide pentagonal | ||
|---|---|---|
| Familia: Sólido de Johnson | ||
 Imagen del sólido | ||
| Tipo | Johnson J1 - J2 - J3 | |
| Caras | 5 triángulos1 pentágono | |
| Aristas | 10 | |
| Vértices | 6 | |
| Configuración de vértices | 5(32.5) (35) | |
| Grupo de simetría | C5v | |
| Poliedro dual | autodual | |
| Propiedades | ||
| Convexo | ||
| Desarrollo | ||
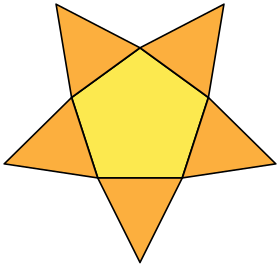 | ||
Ejemplo
En geometría, una pirámide pentagonal es una pirámide de base pentagonal sobre la cual se sobresalen cinco caras triangulares que se encuentran en un punto, la cúspide. Al igual que cualquier pirámide, es autodual. Este poliedro tiene 6 caras, 10 aristas y 6 vértices.
Área y volumen
[editar]El área de una pirámide pentagonal de altura y cuya base es un pentágono regular de lado es[1]
Y su volumen es
Sólido de Johnson
[editar]La pirámide pentagonal regular tiene una base que es un pentágono regular y caras laterales que son triángulos equiláteros. Es uno de los sólidos de Johnson (J2). Su altura H, medida desde el punto central de la cara pentagonal hasta la cúspide, mide[2]
donde L es la longitud de cualquiera de sus aristas.
El área de la pirámide es
Y el volumen es
Puede considerarse la "tapa" de un icosaedro; el resto del icosaedro forma una pirámide pentagonal giroelongada, J11. Los 92 sólidos de Johnson fueron nombrados y descritos por Norman Johnson en 1966.
De forma más general, una pirámide pentagonal isogonal puede construirse a partir de una base pentagonal regular y 5 lados triangulares isósceles de cualquier altura.
Poliedros relacionados
[editar]| Pirámides | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Cuadrada | Pentagonal | Hexagonal | Heptagonal | Octogonal | Eneagonal | Decagonal... |
| Impropia | Regular | Equilátera | Isósceles | |||||
 |  |  |  | |||||
 |  |  |  |  |  |  |  |  |
Véase también
[editar]Referencias
[editar]- ↑ Sapiña, R. «Área y volumen de una pirámide pentagonal y del sólido de Johnson J₂». Problemas y ecuaciones. ISSN 2659-9899. Consultado el 29 de junio de 2020.
- ↑ Weisstein, Eric W. «Pirámide pentagonal». mathworld.wolfram.com (en inglés). Consultado el 29 de junio de 2020.
Enlaces externos
[editar]- Weisstein, Eric W. «Johnson solid». En Weisstein, Eric W, ed. MathWorld (en inglés). Wolfram Research.
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra ( VRML


 French
French Deutsch
Deutsch





