Sólido casi coincidente de Johnson , la enciclopedia libre
En geometría, un sólido casi coincidente de Johnson es un poliedro convexo cuyas caras están cerca de ser polígonos regulares, pero algunas o todas ellas no son exactamente regulares. Por lo tanto, no cumple con la definición estricta de sólido de Johnson, que debe ser un poliedro cuyas caras son todas regulares. En el caso de los sólidos casi coincidentes de Jonshon "a menudo es posible construirlos físicamente sin a penas notar la discrepancia" entre sus caras regulares y sus caras irregulares.[1] El grado exacto de irregularidad depende de lo cerca que se requiera que las caras de dicho poliedro deban aproximarse a polígonos regulares. Algunos casos de alta simetría también son simetroedros con algunas caras poligonales regulares perfectas.
Ejemplos
[editar]| Nombre Nombre de Conway | Imagen | Configuraciones de vértices | V | A | C | C3 | C4 | C5 | C6 | C8 | C10 | C12 | Simetría |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bipirámide triangular truncada t4dP3 |  | 2 (5.5.5) 12 (4.5.5) | 14 | 21 | 9 | 3 | 6 | Dih3 orden 12 | |||||
| Triaquis tetraedro truncado t6kT |  | 4 (5.5.5) 24 (5.5.6) | 28 | 42 | 16 | 12 | 4 | Td, [3,3] orden 24 | |||||
| Piritoheptacontatetraedro pentahexagonal |  | 12 (3.5.3.6) 24 (3.3.5.6) 24 (3.3.3.3.5) | 60 | 132 | 74 | 56 | 12 | 6 | Th, [3+,4] orden 24 | ||||
| Cubo achaflanado cC |  | 24 (4.6.6) 8 (6.6.6) | 32 | 48 | 18 | 6 | 12 | Oh, [4,3] orden 48 | |||||
| - |  | 12 (5.5.6) 6 (3.5.3.5) 12 (3.3.5.5) | 30 | 54 | 26 | 12 | 12 | 2 | D6h, [6,2] orden 24 | ||||
| - | 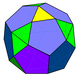 | 6 (5.5.5) 9 (3.5.3.5) 12 (3.3.5.5) | 27 | 51 | 26 | 14 | 12 | D3h, [3,2] orden 12 | |||||
| Dodecaedro tetrado |  | 4 (5.5.5) 12 (3.5.3.5) 12 (3.3.5.5) | 28 | 54 | 28 | 16 | 12 | Td, [3,3] orden 24 | |||||
| Dodecaedro achaflanado cD |  | 60 (5.6.6) 20 (6.6.6) | 80 | 120 | 42 | 12 | 30 | Ih, [5,3] orden 120 | |||||
| Icosaedro truncado rectificado atI |  | 60 (3.5.3.6) 30 (3.6.3.6) | 90 | 180 | 92 | 60 | 12 | 20 | Ih, [5,3] orden 120 | ||||
| Icosaedro truncado truncado ttI |  | 120 (3.10.12) 60 (3.12.12) | 180 | 270 | 92 | 60 | 12 | 20 | Ih, [5,3] orden 120 | ||||
| Icosaedro truncado expandido etI |  | 60 (3.4.5.4) 120 (3.4.6.4) | 180 | 360 | 182 | 60 | 90 | 12 | 20 | Ih, [5,3] orden 120 | |||
| Icosaedro truncado rectificado achatado stI |  | 60 (3.3.3.3.5) 120 (3.3.3.3.6) | 180 | 450 | 272 | 240 | 12 | 20 | I, [5,3]+ orden 60 |
Caras coplanares
[editar]Algunos candidatos a sólidos casi coincidentes de Johnson tienen caras coplanares. Estos poliedros se pueden deformar para volverse convexos con caras que estén arbitrariamente cerca de polígonos regulares. En estos casos se utilizan figuras de vértice 4.4.4.4 del teselado cuadrado, figuras de vértice 3.3.3.3.3.3 del teselado triangular, así como rombos de 60 grados divididos en caras de triángulos equiláteros dobles, o un trapezoide de 60 grados formado por tres triángulos equiláteros. Es posible tomar una cantidad infinita de formas coplanares distintas sobre las secciones de un panal cúbico (alternativamente, de un policubo convexo) o de un panal cúbico alternado, ignorando las divisiones entre caras coplanares.
Ejemplos: 3.3.3.3.3.3
- Prisma rómbico
- Pirámide trigonal giroelongada
- Tetraedro monorrectificado triangulado
- Octaedro, tetraedro triangulado
- Cúpula triangular aumentada
- Bipirámide triangular truncada triangulada
4.4.4.4
3.4.6.4:
- Cúpula hexagonal
(Degenerada)
Véase también
[editar]Referencias
[editar]- ↑ Kaplan, Craig S.; Hart, George W. (2001), «Symmetrohedra: Polyhedra from Symmetric Placement of Regular Polygons», Bridges: Mathematical Connections in Art, Music and Science, archivado desde el original el 23 de septiembre de 2015, consultado el 26 de octubre de 2022..


 French
French Deutsch
Deutsch