اپی گراف - ویکی‌پدیا، دانشنامهٔ آزاد

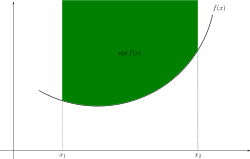
در ریاضیات اپی گراف یا سوپر گراف تابعی از f:Rⁿ→R مجموعه‌ای واقع یا بالای یک تابع است که به صورت زیر تعریف می‌شود:^[۱]

${\displaystyle {\mbox{epi}}f=\{(x,\mu )\,:\,x\in \mathbb {R} ^{n},\,\mu \in \mathbb {R} ,\,\mu \geq f(x)\}\subseteq \mathbb {R} ^{n+1}.}$

و اپی گراف اکید یا مؤکد به صورت زیر تعریف می‌شود:

${\displaystyle {\mbox{epi}}_{S}f=\{(x,\mu )\,:\,x\in \mathbb {R} ^{n},\,\mu \in \mathbb {R} ,\,\mu >f(x)\}\subseteq \mathbb {R} ^{n+1}.}$

که شامل خود تابع نمی‌شود. مشابها تابع هایپوگراف مجموعه‌ای است که واقع یا زیر یک تابع را شامل می‌شود.

${\displaystyle {\mbox{hyp}}f=\{(x,\mu )\,:\,x\in \mathbb {R} ^{n},\,\mu \in \mathbb {R} ,\,\mu \leq f(x)\}\subseteq \mathbb {R} ^{n+1}.}$

در یک تابع محدب اپی گراف محدب است و همچنین اگر اپی گراف یک تابع محدب باشد خود تابع نیز محدب است. در حقیقت اپی گراف ارتباط دهنده توابع محدب و مجموعه‌های محدب است. اگر مجموعه هایپوگراف یک تابع محدب باشد تابع f یک تابع مقعر است و همچنین اگر اپی گراف یک تابع محدب باشد خود تابع مقعر است.

• بهینه‌سازی محدب
• اپی گراف
• تابع محدب

1)Boyd, Stephen and Lieven Vandenberghe. Convex Optimization. ISBN 0-521-83378-7

2)Nef, Walter (1988-01-01). Linear Algebra (in English). Courier Corporation. p. 35. ISBN 978-0-486-65772-1