بیضی‌گون - ویکی‌پدیا، دانشنامهٔ آزاد

در هندسهٔ تحلیلی، بیضی‌گون^[۱][۲][۳] (به انگلیسی: Ellipsoid) یا بیضی‌وار^[۴] یک رویهٔ کران‌دار و یکی از انواع رویه‌های درجهٔ دوم است.^[۵] بیضی‌گون را می‌توان حاصل دِفُرمه کردن یک کره تصور کرد.

هر سطح مقطع از بیضی‌گون یا یک بیضی است، یا یک نقطه یا تهی.^[۶] به همین دلیل است که بیضی‌گون (به معنی شبیه بیضی) نامگذاری شده.

بیضی‌گون سه محور (خط) تقارن دارد که همگی برهم عمود و در یک مرکز (نقطه) تقارن (مرکز بیضی) با یکدیگر متقاطع هستند.

سه پاره‌خط محدود در بیضی و روی محورهای تقارنش را قطرهای بیضی می‌نامند.

حجم بیضی‌گون به کمک فرمول ${\displaystyle {4 \over 3}\pi abc}$ زیر به دست می‌آید.

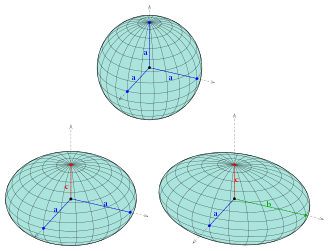
• اگر دو تا از قطرهای بیضی‌گون برابر باشند، به آن کره‌وار نیز می‌گویند که از دوران یک بیضی به دست می‌آید.
• اگر هر سه قطر بیضی با یکدیگر برابر باشند، به آن کره می‌گویند.

در دستگاه مختصات دکارتی، روش استاندارد نمایش بیضی‌گون با قطرهای ${\displaystyle 2a}$ و ${\displaystyle 2b}$ و ${\displaystyle 2c}$ و با مرکز در مبدأ مختصات به صورت زیر است:^[۵]

${\displaystyle {x^{2} \over a^{2}}+{y^{2} \over b^{2}}+{z^{2} \over c^{2}}=1}$

بیضی‌گون یک رویهٔ درجه دو است. یک ابربیضی‌گون در فضای ${\displaystyle \mathbb {R} ^{n}}$، یک ابررویهٔ درجه دو است.

یک ابربیضی‌گون با مرکز در مبدأ مختصات شعاع‌های ${\displaystyle c_{1},c_{2},\dots ,c_{n}}$، مکان هندسی نقاطی مانند ${\displaystyle P=(x_{1},x_{2},\dots ,x_{n})}$ است که در معادلهٔ استاندارد زیر صدق کنند:

${\displaystyle {x_{1}^{2} \over c_{1}^{2}}+{x_{2}^{2} \over c_{2}^{2}}+\dots +{x_{n}^{2} \over c_{n}^{2}}=1}$

محاسبهٔ حجم ابربیضی‌گون شبیه بیضی‌گون است.

• بیضی
• بیضی‌وار مرجع
• رویه
• ابر رویهٔ درجهٔ دوم

در ویکی‌انبار پرونده‌هایی دربارهٔ بیضی‌گون موجود است.