کاهش غیرخطی ابعاد - ویکیپدیا، دانشنامهٔ آزاد

تفسیر دادههای دارای ابعاد بالا، یعنی دادههایی که نیاز به بیش از ۲ یا ۳ بعد برای نمایش دادهشدن دارند، دشوار است. یک راه برای سادهسازی این است که فرض کنیم دادهها روی یک خمینه غیرخطی نهفته در فضای مورد نظر قرار دارند. اگر بعد خمینه به مقدار کافی کم باشد، دادهها را میتوان در این فضای با ابعاد پایینتر نشان داد.
بسیاری از الگوریتمهای کاهش غیرخطی ابعاد با روشهای خطی زیر ارتباط دارند:
- تحلیل مؤلفههای مستقل (ICA)
- تحلیل مؤلفههای اصلی (PCA)
- تجزیه مقدارهای منفرد (SVD)
- آنالیز عاملها (Factor Analysis)
روشهای غیرخطی را میتوان به دو دسته عمده تقسیم کرد:
آنهایی که یک نگاشت (از فضای با ابعاد بالاتر به خمینهٔ نهفته با ابعاد پایینتر با برعکس)(mapping) هستند، و آنهایی که تنها یک نمایش از دادهها ارائه میکنند. در زمینهٔ یادگیری ماشینی، روشهای نگاشت به عنوان مرحلهٔ استخراج ویژگی، پیش از اعمال الگوریتمهای شناسایی الگو استفاده میشوند. آنهایی که یک نمایش از دادهها ارائه میکنند، بر اساس دادههای مجاورت ـ فاصله بین نقاط) ـ هستند.
کاربردهای کاهش غیرخطی ابعاد
[ویرایش]فرض کنید در یک تسک یادگیری ماشین، مجموعه داده را به صورت یک ماتریس در اختیار دارید به گونه ای که هر کدام از m سطر یک نقطه داده دارای n متغیر (یا ویژگی یا بعد) است. در صورتی که تعداد ویژگیها زیاد باشد، فضای نقطه دادههای ممکن به صورت نمایی زیاد میشود که به این پدیده مشقت بعدچندی گفته میشود. بهطور مثال اگر هر کدام از متغیرها دارای مقدار مختلف باشد، پیکربندی متفاوت را میتوان برای فضای ورودی متصور شد.
یکی از مشکلاتی که این پدیده به همراه دارد یک چالش آماری است. فرض کنید فضای ورودی به صورت یک توری (grid) سازماندهی شدهاست. یک فضا با ابعاد کم را با تعداد کمی نقطه داده میتوان توصیف کرد. بهطور مثال برای تخمین توزیع احتمال در یک نقطه دلخواه کافی است تعداد نقطهدادههایی که با نقطه مورد نظر در یک خانه (مکعب واحد شامل ) هستند را تقسیم بر تعداد کل نمونههای آموزشی کرد، یا برای تسک طبقهبندی کافی است یک رایگیری حداکثری بین دادههای آموزشی در خانه مورد نظر انجام دهیم. اما هرچه ابعاد ورودی بزرگتر میشود، تعداد دادههای آموزش مورد نیاز بهطور نمایی افزایش مییابد. این چالش آماری الگوریتمهای یادگیری ماشین را مستلزم میکند که برای تعمیم به نقطهدادههای جدید در فضای ورودی، مجموعه دادگان عظیمی داشته باشند که در عمل دستنیافتنی است. این یکی از انگیزههای پیگیری الگوریتمهای یادگیری ژرف است که عموماً بر روی دادههای با ابعاد بالا از جمله متن و تصویر بهتر عمل میکنند.[۱] یکی دیگر از مشکلات ابعاد بالای ورودی عدم امکان درکشدن توسط انسانها و مصورسازی دادهها به صورت مستقیم است. این دو مشکل بیانشده انگیزه را برای کاهش غیرخطی ابعاد فراهم میآورد.[۲]
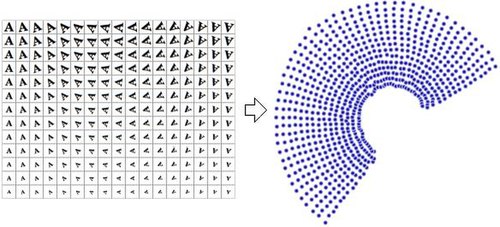
به بازنمایی دادگان بعد از اعمال کاهش ابعاد عموماً «متغیرهای ذاتی» میگویند. به عبارت دیگر، این متغیرها مشخص میکنند که دادگان چگونه تولید شدهاند و روند تولید دادگان را مدل میکنند. بهطور مثال در تصویر سمت چپ متغیرهای ذاتی عبارتند از چرخش و مقیاس در حالی که متغیرهای ورودی پیکسلهای تصویر ۳۲*۳۲ هستند؛ یعنی بعد ورودی ۱۰۲۴ است. کاهش غیرخطی ابعاد اطلاعات دارای همبستگی را از بین میبرد (تصویر حرف A که در همهٔ ورودیها وجود دارد، فقط دچار چرخش یا تغییر مقیاس شدهاست) و اطلاعات متغیر را بازیابی میکند (چرخش و مقیاس). تصویر سمت راست تبدیل یافته ورودیها در صفحه دوبعدی نمایش میدهد.

علت استفاده از تبدیل غیرخطی این است که در اکثر مواقع بین متغیرهای ورودی و متغیرهای ذاتی رابطه ای غیر خطی وجود دارد. بهطور مثال اگر از تحلیل مولفههای اصلی که یک روش کاهش خطی ابعاد است برای تبدیل ورودیها استفاده کنیم، متغیرهای حاصل سازمانمند نخواهند بود که به دلیل خطای بالای حاصل از بازتولید ورودی از فضای ذاتی خواهد بود چرا که به خوبی نمیتوان با یک مدل خطی این فضای ورودی را تخمین زد.
در نتیجه میتوان از روشهای کاهش غیرخطی ابعاد در شاخههایی از یادگیری ماشین که ابعاد ورودی بزرگ هستند استفاده کرد، به این صورت که ابتدا ابعاد ورودی را به دلخواه کاهش داد، بدون این که متغیرهای ذاتی (در صورت وجود) زیادی حذف شوند، و سپس الگوریتمهای یادگیری روی مجموعه دادگان در فضای ذاتی اجرا شوند. همچنین میتوان از این روشها برای مصورسازی مجموعه دادگان استفاده کرد به این صورت که ورودیها را به ابعاد ۲ یا ۳ کاهش داده و سپس در فضای جدید ترسیم کرد.
جستارهای وابسته
[ویرایش]- آنالیز افتراقی خطی
- یادگیری ویژگی
- نقشههای خودسازماندهنده (SOM)
- مشقت بعدچندی
- مصورسازی داده
- یادگیری ژرف
پیوند به بیرون
[ویرایش]- Isomap
- Generative Topographic Mapping
- Mike Tipping's Thesis
- Gaussian Process Latent Variable Model
- Locally Linear Embedding
- Relational Perspective Map
- Waffles is an open source C++ library containing implementations of LLE, Manifold Sculpting, and some other manifold learning algorithms.
- DD-HDS homepage
- RankVisu homepage
- Short review of Diffusion Maps
- Nonlinear PCA by autoencoder neural networks
منابع
[ویرایش]- ↑ Haller, George; Ponsioen, Sten (2016-11). "Nonlinear normal modes and spectral submanifolds: existence, uniqueness and use in model reduction". Nonlinear Dynamics (به انگلیسی). 86 (3): 1493–1534. doi:10.1007/s11071-016-2974-z. ISSN 0924-090X.
{{cite journal}}: Check date values in:|date=(help) - ↑ Goodfellow، Ian (۲۰۱۶). Deep Learning [یادگیری ژرف]. بایگانیشده از اصلی در پارامتر
|پیوند بایگانی=نیاز به وارد کردن|تاریخ بایگانی=دارد (کمک).
- مشارکتکنندگان ویکیپدیا. «Nonlinear dimensionality Reduction». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۲۰ اردیبهشت ۱۳۹۲.


 French
French Deutsch
Deutsch


