فرایند تولد-مرگ - ویکیپدیا، دانشنامهٔ آزاد
فرایند تولد مرگ (زاد مرگ) صورت خاصی از فرایند مارکف زمان گسسته است که در آن تغییر حالتها تنها از دو نوع است:
- تولد: در این حالت مقدار وضعیت ۱ واحد افزایش مییابد.
- مرگ: در این حالت مقدار وضعیت ۱ واحد کاهش مییابد.
اسم مدل از کاربردهای معمول میآید٬مانند زمانی که استفاده از این مدلها برای نشان دادن سایز فعلی جمعیت و مدلی از مرگ و تولد به معنای واقعی به کار میرود. فرایندهای زاد و مرگ کاربردهای زیادی در آمارنگاری مردم٬تئوری صف٬مهندسی کارائی٬علم امراض مسری یا در زیستشناسی دارد. این روش میتواند در کاربرد هائی نظیر مطالعهٔ تکامل باکتری ها٬تعداد مردم با وجود یک بیماری در جمعیت٬یا تعداد مشتریها در یک صف سوپرمارکت استفاده شود.
هنگامی که تولد رخ میدهد فرایند از حالت n به n + 1 میرود. هنگامی که مرگ رخ میدهد فرایند از حالت n به حالت n − 1 میرود. این فرایند را میتوان با نرخ تولدو نرخ مرگمشخص نمود.
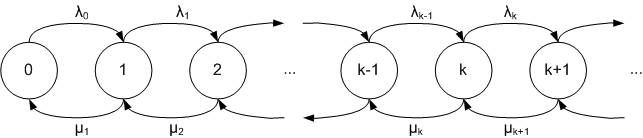
نمونههایی از فرایند زاد-مرگ
[ویرایش]یک فرایند زاد-مرگ را یک فرایند تولد خالص مینامیم اگر در آن برای همهٔ داشته باشیم .
یک فرایند زاد-مرگ را یک فرایند مرگ خالص مینامیم اگر در آن برای همهٔ داشته باشیم .
فرایند پواسون (همگن) حالتی خاصی از فرایند زاد-مرگ خالص است که برای آن داشته باشیم .
مدل M/M/1 و مدل M/M/c که هر دو در تئوری صف استفاده شدهاند، فرایند تولد مرگی هستند که برای توصیف مشتریان در صف نامحدود استفاده میشوند.
استفاده در تئوری صف
[ویرایش]در تئوری صف فرایند تولد مرگ یکی از اساسیترین مثالهای مدل صف بندی M/M/C/K//FIFO/(در علامتگذاری کامل kandell) است. این یک صف با ورود پواسون است که از یک جمعیت بینهایت که از C سرویسرسان با زمان سرویس توزیع نمائی با K مکان استفاده میکند. به رغم فرض جمعیت نامحدود، این مدل یک مدل خوب برای سیستمهای مخابراتی متنوع است.
صف M/M/1
[ویرایش]M/M/1 یک صف سرویسرسانی منفرد از اندازه بافر بینهایت است. در محیط غیر تصادفی، فرایند تولد مرگ در مدل صف بندی تمایل دارد که با میانگین بلند مدت باشد٬بنابراین نرخ میانگین ورودها به صورت و متوسط زمان سرویس دهی به صورت میباشد. فرایند تولد و مرگ یک صف M/M/1 است زمانی که داشته باشیم:
معادلهٔ تفاضلی برای این احتمال که سیستم در حالت k و در زمان t باشند به صورت زیر بیان میشود.
صف M/M/c
[ویرایش]M/M/c چندین صف با C سرور و بافر نامحدود است. این حالت با M/M/1 تنها در زمان سرویس متفاوت است که اکنون به صورت زیر محاسبه خواهد شد.
و
با
صف M/M/1/K
[ویرایش]M/M/1/K یک صف سرور سرویسرسانی منفرد با بافری از اندازی K است. این صف در مخابرات و همچنین زیستشناسی هنگامی که محدودیتی بر روی ظرفیت داریم استفاده میشود. در مخابرات ما دوباره از پارامترهایی که از صف M/M/1 بدست میآیند٬به صورت استفاده میکنیم.
در زیستشناسی به خصوص در مبحث رشد باکتریها زمانی که جمعیت صفر است هیچ توانایی برای رشد نیست بنابراین داریم
علاوه بر این اگر ظرفیت نشان دهندهٔ محدودیت باشد مثلاً در جایی که جمعیت از جمعیت زیاد بمیرند داریم:
معادلات دیفرانسیل برای احتمال این که سیستم در حالت k در زمان t باشد به صورت زیر است:
تعادل
[ویرایش]یک صف گفته میشود که در تعادل است٬اگر حد وجود داشته باشد. برای این مورد باید صفر باشد.
اگر صف M/M/1 را فرض بگیریم٬پاسخ حالت دائم (تعادل) به صورت زیر است:
اگر برای همه داشته باشیم: و (حالت همگن) این فرض میتواند به معادله زیر بینجامد.
رفتار محدود
[ویرایش]در یک زمان کوچک تنها سه نوع از انتقال امکانپذیر است: یک مرگ یا یک تولد یا نه مرگ و نه تولد. اگر نرخ وقوع (در واحد زمان) تولد باشد برای مرگ باشد. سپس احتمالات جابجائی به ترتیب , و میباشد. برای یک فرایند جمعیت «تولد» انتقال به سمت افزایش جمعیت به مقدار ۱ است در حالی که «مرگ» انتقال به سمت کاهش اندازهٔ جمعیت به مقدار ۱ است.
جستارهای وابسته
[ویرایش]منابع
[ویرایش]- G. Latouche, V. Ramaswami. Introduction to Matrix Analytic Methods in Stochastic Modelling, 1st edition. Chapter 1: Quasi-Birth-and-Death Processes; ASA SIAM, 1999.
- M. A. Nowak. Evolutionary Dynamics: Exploring the Equations of Life, Harvard University Press, 2006.
- J. Virtamo,"Birth-death processesBirth-death processes"[۱], 38.3143 Queueing Theory.


 French
French Deutsch
Deutsch


































