Épitrochoïde — Wikipédia

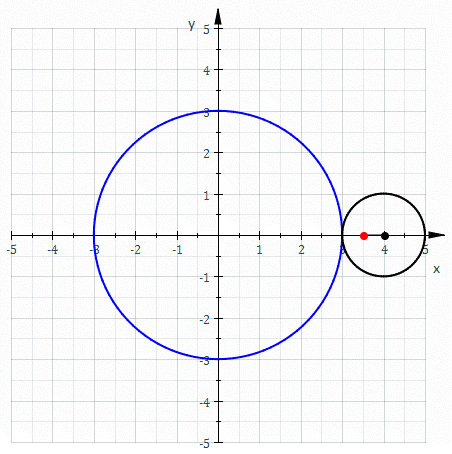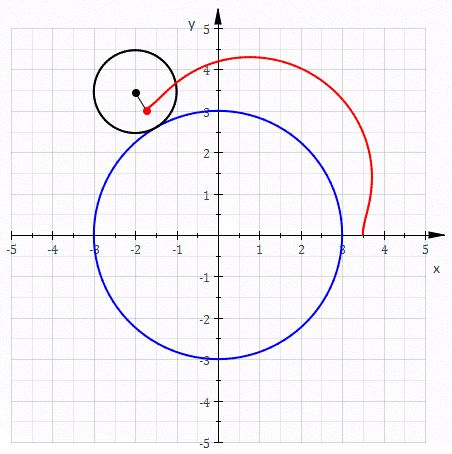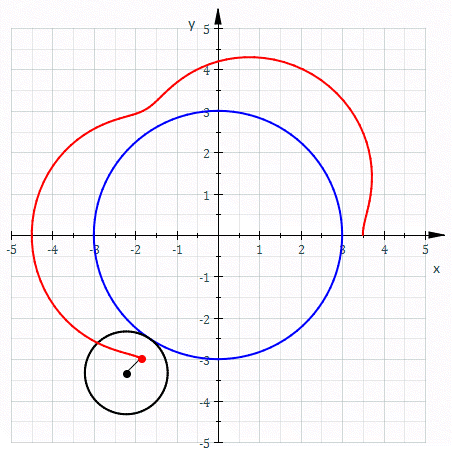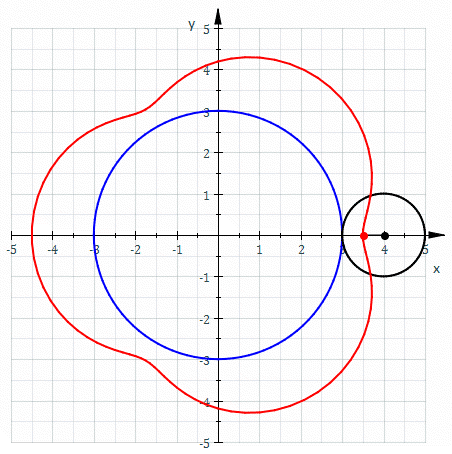
Une épitrochoïde est une courbe plane transcendante, correspondant à la trajectoire d'un point fixé à un cercle mobile qui roule sans glisser sur et autour d'un autre cercle dit directeur.

${\displaystyle x=(R+r)\cos \theta -d\cos \left({R+r \over r}\theta \right),\,}$

${\displaystyle y=(R+r)\sin \theta -d\sin \left({R+r \over r}\theta \right).\,}$

où R est le rayon du cercle directeur, r celui du cercle mobile, d la distance du point au centre du cercle mobile et ${\displaystyle \theta }$ le paramètre d'angle.

Toute épicycloïde de paramètres R, r, d est équivalente à une péritrochoïde de paramètres ${\displaystyle {\begin{array}{lll}R'={d \over r}R,&r'={d \over r}(R+r),&d'=R+r\end{array}}}$.

Par péritrochoïde, on entend la courbe obtenue à l'aide d'un point lié à un cercle mobile roulant sans glisser autour d'un cercle directeur qu'il contient, soit une « hypotrochoïde » pour laquelle ${\displaystyle r>R}$.

L'enceinte du moteur Wankel représente en coupe une épitrochoïde/péritrochoïde.

• Lorsque le point est situé sur le cercle mobile (${\displaystyle d=r}$), on obtient une épicycloïde^[1].
• Quand les deux cercles sont de même rayon (${\displaystyle R=r}$), l'épitrochoïde représente un limaçon de Pascal, voire une cardioïde si ${\displaystyle d=r}$.
• Pour ${\displaystyle d=R+r}$, on obtient une rosace.

• Épicycloïde
• Hypotrochoïde
• Spirographe

• « Epitrochoïde », sur Mathcurve.com: Encyclopédie des formes mathématiques remarquables

• Portail de la géométrie