Adrien Romain — Wikipédia

Vous lisez un « article de qualité » labellisé en 2010.

Adrien Romain

Biographie

Naissance	29 septembre 1561 Louvain (Dix-sept Provinces)
Décès	4 mai 1631 (à 69 ans) Mayence (Saint-Empire romain germanique)
Formation	Université de Cologne Ancienne université de Louvain
Activités	Mathématicien, professeur

Autres informations

A travaillé pour	Université de Wurtzbourg (1593-1607) Ancienne université de Louvain (1586-1592)

Plaque commémorative

modifier - modifier le code - modifier Wikidata

Adriaan van Roomen, qui latinisait son nom en Adrianus Romanus, francisé en Adrien Romain, né à Louvain (Région flamande de Belgique), le 29 septembre 1561, mort à Mayence (Allemagne) le 4 mai 1615, est un médecin et mathématicien.

Il devient le premier professeur de médecine rémunéré de l'université de Würzburg^[1], et le médecin personnel de l'évêque Julius Echter de Mespelbrunn.

Scientifique éclectique, ses domaines de prédilection varient de la géographie aux sciences physiques. Il est l'un des premiers à décrire les feux d'artifice, mais c'est dans le domaine des mathématiques qu'il s'illustre le plus.

Prodigieux calculateur, l'un des plus remarquables de tous les temps selon son principal commentateur Henri Bosmans^[2], Adrien Romain effectue de nombreux travaux mathématiques. Élève de Stevin et Sarpi, il côtoie la plupart des scientifiques de son temps, qui le tiennent en grande estime, dont François Viète, Johannes Kepler, le P. Clavius, Marino Ghetaldi, Ludolph van Ceulen dont il est l'ami personnel, Willebrord Snell et Michel Coignet.

Adrien Romain s'oppose avec succès à l'humaniste Scaliger, recteur de l'université de Leyde, en mettant en évidence ses erreurs de quadrature du cercle. Il propose à ses confrères européens un défi mathématique resté fameux, et doit en retour relever un défi de François Viète dont il ne peut triompher par une construction à la règle et au compas. Son écriture mathématique est à mi-chemin de l'école de la Coss, dont il est issu, et de l'algèbre nouvelle de Viète, dont il se montre un des meilleurs héritiers dans certains de ses travaux algébriques, avec Alexander Anderson, Marino Ghetaldi, Albert Girard et Jacques Aleaume. Il est le premier mathématicien européen à calculer 16 décimales de π.

Né le 29 septembre 1561, probablement à Louvain, Adriaan van Roomen est le fils d'un marchand^[3], dont il porte le nom et le prénom, d'une famille qui serait originaire de Berg-op-Zoom^[4],[5]. On lui connaît un frère Jan, qui sera chirurgien à Huy, et une sœur Maria. De sa jeunesse rien n'est parvenu^[4]. Il étudie les langues anciennes dans sa ville natale, puis la philosophie, les mathématiques et l'astronomie au collège jésuite de Cologne^[6]. En 1585, il effectue un voyage en Italie, au cours duquel il rencontre Christophorus Clavius, et demeure en correspondance avec lui, puis il se spécialise en médecine à l'université de Louvain.

De 1586 à 1592 Adrien Romain enseigne la médecine à Huy^[6], puis à Louvain où il professe aussi les mathématiques à l'université. En 1593, il publie Ideae mathematicae pars prima, sive methodus polygonorum^[7], donnant la valeur de π (il n'utilise pas cette notation) avec seize décimales dont la dernière est inexacte^[8], soit au-delà de ce que Viète avait réalisé en 1579 dans son Canon mathématique.

Son ouvrage est dédié au père Clavius, dont il fait le plus grand éloge, ainsi qu'aux mathématiciens de son temps Michel Coignet^[9], Nicolas Peterseen et Simon Stevin. Il écrit plus tard de cette époque de sa vie^[6] :

« Je m'étais mis en tête de dresser un projet de mathématiques universelles, pour me rendre bien compte de ce que cette science, reine de toutes les sciences, embrasse dans son domaine. »

Pendant ces premières années, Adrien Romain publie quelques traités d'arithmétique, aujourd'hui perdus. Il se lie d'amitié avec Ludolph van Ceulen, qui selon ses mots fut « le premier de tous les arithméticiens qui sont et qui furent jamais ». Il forme de nombreux étudiants dont certains sont invités à relever le défi lancé dans les Idea^[10], d'Anvers, Corneille Opmeer de Delft, auxquels il rend ultérieurement hommage.

En 1590, ayant gagné le titre de maître-es-arts et licencié de médecine^[11], il fait éditer chez Jean Keerberg de Louvain son Uranographie, traité de vulgarisation de la cosmographie. En 1592, il occupe pendant six mois le poste de recteur. Parmi ses collègues et amis de Louvain, se trouvent le linguiste François Ravlenghien (Raphelengius, 1539-1597) et le médecin botaniste Charles de L'Écluse. Les troubles qui animent alors la Flandre, déjà déchirée par des guerres de religion, le poussent à fuir sous des cieux plus cléments^[12].

Le dernier jour d'août 1593, il se voit confier par le très catholique Jules Echter von Mespelbrunn, duc de Franconie et prince-évêque de Würzburg, la chaire de médecine à l'université de cette ville, recréée dix ans plus tôt sous l'impulsion de celui-ci ; la nouvelle université est un fer de lance de la Contre-Réforme^{[Notes 1]}, elle compte déjà plus de 1 000 étudiants^[13],[14]. La même année il se marie avec Anna Steegh d'Amerfort, nièce de Godefroy Steegh, médecin ordinaire du prince^[6]. À l'été 1594, il est en Italie où, le 8 juillet, il obtient le titre de docteur en médecine à l'université de Bologne^[15] ; la même année il publie la thèse d'un étudiant défendue sous sa présidence^[16] et montre son érudition lors de la réception du docteur Henning Scheunemann^[17].

Dans une lettre de janvier 1594 adressée au prince-évêque de Würzburg, son mécène, Romain décrit avec force louanges trois ouvrages dont il souhaite certainement lui voir financer la publication^[19]. Pour le premier, un traité universel des langues, il ne prétend pas à l'originalité, contrairement aux deux autres consacrés aux mathématiques, le Summum geometriae cacumen (plus haut sommet de la géométrie) et l'Astronomiae nova methodus (nouvelle méthode pour l'astronomie) :

« Illustrissime Prince, outre l'ouvrage sur les langues dont je vous ai parlé récemment, j'en ai écrit deux autres sur les mathématiques (...) J'ai tiré mes ouvrages de mathématiques de mon propre fonds et l'on n'y pourrait trouver une seule lettre empruntée à des livres étrangers : je puis les revendiquer absolument comme miens. (...) Il me siérait mal en effet de me donner pour versé dans toutes les langues, moi qui ne possède même pas suffisamment ma langue maternelle (...) [et] tout l'ouvrage est extrait à force de recherche et de travail d'une foule d'auteurs, (...) traductions, commentaires, scholies de divers ouvrages anciens (...) que je me suis vu forcé d'acquérir à grands frais, [ou] que j'ai pu obtenir en échange de quelques bibliothèques. Aucun de tous ces livres ne m'a servi pour mes ouvrages de mathématiques qui sont en entier le fruit de mon esprit^[20]. »

Le Summum geometriae cacumen est consacré au calcul de l'aire du cercle et à la trigonométrie plane et sphérique, l'Astronomiae nova methodus décrit de « nouvelles règles astronomiques et de nouvelles tables » ainsi que « la construction de tous les instruments d'astronomie »^[21]. Aucun de ses ouvrages n'est publié, on ne trouve rien dans ses œuvres ultérieures au sujet de la linguistique et peu concernant l'astronomie^[22].

En octobre 1594, Romain produit également son premier calendrier calculé selon l'ancien style et le nouveau, le Theoria calendariorum^[23], où il se nomme lui-même Eques auratus^{[Notes 2]}.

En 1595, par amitié pour le mathématicien épéiste et génial calculateur Ludolph van Ceulen, il fait publier un défi aux mathématiciens du monde entier (c'est-à-dire l'Europe)^[24], où il leur propose de résoudre une équation de degré 45, posée dans un langage propre à Stevin, et voisin de la Coss.

Ce défi ne s'adresse à aucun mathématicien français ; Guillaume Gosselin et Jacques Peletier du Mans sont morts, Maurice Bressieu est méconnu et Henri de Monantheuil est plutôt un médecin. Il est spontanément relevé par le maître des requêtes François Viète^[25], qui en triomphe et donne immédiatement deux solutions, puis quelques jours après les 21 autres solutions positives, à 8 décimales près^[26].

Romain reçoit en retour du mathématicien - amateur - français un problème de géométrie réclamant de tracer un cercle tangent à trois cercles donnés. Ce problème, déjà connu d'Apollonius de Perge, se trouvait dans son traité (perdu) Des contacts. Romain y répond rapidement par une intersection avec une hyperbole auxiliaire et publie son résultat en 1596. Comme sa résolution ne respecte pas les règles de construction à la règle et au compas fixées par Euclide, Viète lui répond vers 1600 par la publication de son Apollonius gallus. Il en naîtra, semble-t-il, une réelle amitié entre les deux hommes.

Vers 1594, Joseph Juste Scaliger, recteur de l'université de Leyde, fait publier un livre de « cyclotomie »^{[Notes 3]}, où il croit démontrer la quadrature du cercle et donner avec certitude ${\displaystyle \pi ={\sqrt {10}}}$, valeur erronée, déjà reconnue fausse par Viète et Regiomontanus. Adrien Romain publie contre Scaliger divers ouvrages, dont un intitulé Apologia pro Archimede ad clarissimum Josephum Scaligerum. Exercitationes cyclicae contra J. Scaligerum, Orontium Finaeum et Raymarum Ursum, in decem dialogos distinctae^[32], qui détruisent cette prétention. Romain écrit à Juste Lipse, alors à Louvain, des appréciations peu flatteuses quant aux travaux de Scaliger^[33] :

« Scaliger, dit-il, édite, à ce que j'apprends, une correction du calendrier grégorien : m'est avis que c'est lui-même qui mériterait une correction ; il a publié un traité de mathématiques intitulé Elementa cyclometrica^[34] qui ne renferme absolument que des déclamations creuses et des principes faux. »

Vexé, Scaliger pousse ses amis protestants de Genève et de Francfort à interdire la publication et la diffusion de ce livre. Un de ses amis, Jacques Esprinchard, lui écrit de la foire de Francfort^[35] :

« Je suis par la grâce de Dieu arrivé sain et sauf en ceste ville de Francfort, où ayant desjà passé quelques jours et visité à mon aise les boutiques des libraires, je n'ay veu qu'un seul livre contre vous, qui est d'Adrianus Romanus, lequel il dédie à l'empereur. Il est imprimé à Genève, encore qu'au bas l'imprimeur ait mis : à Virtzburg. J'ay parle à quelques honestes gens de Genève, qui m'ont bien au long conté comme le tout s'estoit passé en l'impression dudict livre, et comme monsieur de Bèze et tous vos autres amys allèrent par deux fois à la maison de ville pour s'opposer à cela et empescher que ledict livre ne s'imprimast. »

Le même Jacques Esprinchard n'en rend pas moins visite à Adrien Romain qu'il interroge sur le sujet, ainsi qu'il mentionne une dans une autre lettre à Scaliger^[36] :

« Passant par Wirtzbourg, dit-il, j'allay voir Adrianus Romanus, que j'entretins environ une heure, pendant la moitié de laquelle, l'interroguant de plusieurs choses que je désiray sçavoir touchant tout de ce pays et de l'Académie dudict lieu, il mè sembla fort doux et paisible ; mais, changeant de propos, et venant à parler du livre qu'il avoit faict contre vous, je vis qu'il estait aucunement^[37] battu du mal commun de tous vos adversaires, et qu'il y avoit un peu d'animosité dans son faict. »

Le révérend père Clavius, lui, écrit contre Scaliger ces mots d'une dureté inouïe : « Il m’est possible cependant de t’aimer délivré de tes défauts, même en tant qu’homme dépourvu de toute qualité, comme on dit, et également il ne me serait pas très difficile de ne pas te haïr resté malhonnête, mais ni les hommes, ni Dieu, dont tu accumules contre toi une immense colère, ne pourront supporter quelqu’un qui, menteur et faux mathématicien, trouble, sans foi, aboie contre les gens de bien et les personnes estimées et irrite les gens tranquilles^[38]. ».

De 1596 à 1606, Adrien Romain est chargé de la rédaction de la chronologie, des pronostics, des almanachs et des calendriers populaires du chapitre de Würzburg et de la Franconie. Dans ses dédicaces au prince-évêque, il repousse par avance toutes les critiques :

« Je ne me suis point arrêté aux critiques, aux railleries, aux excessives médisances qu'ils provoquent bien souvent parmi la racaille ignorante : elle ne m'injuriera jamais si fort que je ne la méprise encore davantage. »

Ses sentiments religieux s'approfondissent et il affirme dans l'un de ses pronostics^[39] :

« Non, non, ce ne sont point ces causes qui sont en jeu : ce n'est ni des astres, ni de la défaillance des éléments, ni des rois ou des princes, ni de la décrépitude de l'univers que provient ce que nous avons à souffrir et à endurer, mais c'est bien plutôt de nos péchés si graves, si multipliés, qui excitent le juste courroux et la vengeance du Dieu éternel. »

En 1595, paraît son Portrait des villes du monde ou Parvum theatrum orbium, qu'il compose d'après George Braun (gravures de Franz Hogenberg) et quelques autres cosmographes. En 1596, Romain fait soutenir sa thèse de philosophie à son élève préféré, Christophe Upilio, de Würzburg^{[Notes 4]}, puis à Henning Scheunemann d'Halberstadt. L'année suivante, il publie son In Archimeda circuli et en octobre 1597, il fait soutenir une thèse de médecine à l'un de ses élèves, Jean Faber^{[Notes 5]}. En 1598, il publie celle de Lambert Croppet, un de ses rares élèves mathématicien, originaire de Lyon ; un ouvrage d'astronomie et de trigonométrie qu'il signe pour une part. Les deux années suivantes, il examine et habilite les docteurs de médecine Jean Fuchs, André Dolweg et Nicholas Fischer. Pendant ces années-là, il se lie également d'amitié avec Willebrord Snell. À la même époque, Romain perd son épouse ; ils n'ont pas eu d'enfant, mais Romain a hors mariage deux fils, Jacques, qui l'accompagne dans ses voyages, et Conrad^[4]. Le prince-évêque lui offre peu après un canonicat à la collégiale Saint-Jean de Würzburg^[40].

En 1600, Adrien Romain part pour Prague rencontrer Johannes Kepler, avec lequel il échange plusieurs lettres. L'empereur Rodolphe le fait comte palatin. Adrien Romain se nomme désormais lui-même « Eques auratus, comites Palatinus, medicus caesareus, mathematicus eximius, philosophiae ac medicinae doctor celeberrimus, professor primarius, antecessor celeberrimus » ou encore chevalier émérite, comte palatin, médecin impérial, excellent mathématicien, docteur es philosophie et médecine, professeur distingué aux aïeux renommés. En 1601, il est de retour à Würzburg où il fait soutenir quatre thèses de médecine^{[Notes 6]}. En 1602, il publie son Idea matemateseos universae à propos de la mathesis universalis ainsi qu'un Chordarum arcubus circuli, à propos de la corde des arcs de cercle, ce dernier ouvrage étant dédié au grand maître de l'ordre Teutonique. L'année suivante, il est de nouveau doyen de la faculté et supervise sept thèses (toujours de médecine)^{[Notes 7]}. C'est donc au sommet de la gloire en tant que professeur de médecine qu'il sollicite auprès des autorités de l'université, le 19 mai 1603, une dispense d'enseignement pour pouvoir se consacrer complètement à ses recherches mathématiques. Les autorités le renvoient vers le prince-évêque. Et contre toute attente, celui-ci lui accorde non seulement cette dispense, mais le prend à son service comme médecin personnel. Il le nomme vers cette époque chanoine (canonicus) de la paroisse de Neumünster.

De 1603 à 1607, Romain partage régulièrement ses activités entre Louvain et Würzburg. Ordonné prêtre probablement fin 1604 ou début 1605^[41], il fait paraître sa Mathesis Polemica, un livre de mathématiques militaires, à Francfort en 1605 ; puis il revient à Würzburg, produire ses lettres d'ordination^[6]. En 1606, il publie à Louvain son Speculum Astrologicum ou miroir de l'astrologie. Dans les années suivantes, il alterne son enseignement entre Louvain et Würzburg, où il fait imprimer Mathematica analyseos triomphus, le triomphe de l'analyse mathématique. Mais en 1607, il renonce définitivement à sa chaire^[42].

En octobre 1608 a lieu son installation au chapitre. L'année suivante, il fait paraître à Cologne son Canon triangolorum sphericum, ou livre des triangles sphériques, et se rend à Louvain publier son Triomphus analyseos ; l'impression en est de toute beauté. Ses absences lui sont reprochées et les autorités ecclésiastiques menacent de supprimer ses bénéfices.

« Attendu que M. le docteur Adrianus Romanus, chanoine, fait très rarement acte de présence aux matines, ou même à d'autres offices sacrés, il sera encore une fois admonesté fraternellement à ce sujet ; et si Sa Révérence ne fait cesser ces plaintes et continue à donner aux autres chanoines un exemple préjudiciable, Sa dite Révérence sera privée du bénéfice de présence et du partage des pains et des parts (panumatque divisionum beneficio). »

En juin 1610, il demande la permission de se retirer en Bohème pour aller prendre les eaux à Prague. La ville polonaise de Zamość et son magnat, Jan Zamoyski, chancelier du royaume de Pologne, l'invitent à y venir enseigner les mathématiques ; il demeure là-bas les deux années suivantes, avec quelques interruptions. En 1611, il est de retour à Würzburg, puis en 1613, il est à nouveau en Belgique, où il rédige ses dernières volontés^[43].

Adrien Romain meurt le 4 mai 1615 à Mayence, ville où il faisait étape pour se rendre aux eaux de Spa avant de revenir dans sa ville natale de Louvain. Il meurt dans les bras de son fils naturel Jacques^[6]. Son corps est enterré à Mayence, dans l'église Saint-Quentin. L'église Neumünster de Würzburg abrite une stèle qui lui est dédiée, et sur laquelle sont récapitulées ses contributions aux mathématiques et à l'astronomie^[6].

Son cénotaphe porte ses armes, qui sont « d'or à un chevron de gueule, accompagné en pointe d'un paon rouant de sinople ; le cimier surmonté de deux clefs en croix »^[44].

Par codicille rédigé à Würzburg en 1615, il lègue un de ses cadrans-diviseurs au prince Jules Echter, quelques vêtements et quelques ducats à ses logeurs et amis. Le reste de ses biens va à sa sœur, Marie Van den Brouck, qui est priée de les restituer à son fils naturel^[45].

En 1593, son premier ouvrage scientifique intitulé Ideæ mathematicæ prima sive methodus polygonorum paraît à Anvers. C'est dans ce livre, consacré aux calculs des côtés de polygones réguliers, que Romain défie les mathématiciens de son temps de résoudre une équation du 45^e degré de la forme P(X) = C. Romain donne à titre d'indice une solution pour 3 valeurs particulières de C, le problème étant posé pour une quatrième valeur de cette constante.

Romain donne l'expression algébrique (celle du polynôme P(X) avec les notations précédentes) sous la forme suivante

45 (1) - 3795(3) + 95634(5) - 1138500(7) + 7811375(9) - 34512075(11) + 105306075(13) - 232676280(15) + 384942375(17) - 488494125(19) + 4838418000(21) 3786588000(23) + 236030652(25) - 117679100(27) + 46955700(29) - 14945040(31) + 3764565(33) - 740259(35) + 111150(37) - 12300(39) + 945(41) - 45(43) + 1(45),

il écrit entre parenthèses ce qui est pour nous l'exposant de l'inconnue, ainsi nous écririons les trois premiers termes 45x - 3795 x³ + 95634x⁵ + … . Il s'avère que cette équation peut être interprétée comme celle exprimant dans le cercle unité la longueur de la corde de la 45^e partie d'un angle dont la corde est la constante C, ce qui permet de la résoudre pour les valeurs de celle-ci données par Romain, toutes quatre inférieures à 2.

Le mathématicien français François Viète, invité par le roi Henri IV à résoudre cette énigme, aperçoit immédiatement cette relation, qui lui permet de fournir le jour même une solution^[3]. Il résout le problème de façon élégante, en le décomposant en 3 équations, deux du 3^e degré et une du 5^e (45 = 3²5), et fournit de plus les 23 racines positives (les seules considérées comme recevables par les géomètres de l'époque) tout en mentionnant l'existence de 22 solutions négatives^[46].

Cette anecdote a donné lieu à un récit coloré de Tallemant de Réaux dans ses Historiettes (où il fait à tort du professeur de Louvain un mathématicien hollandais)^[47] :

« Du temps d'Henri IV, un Hollandais, nommé Adrianus Romanus, savant aux mathématiques, mais non pas tant qu'il croyait, fit un livre où il mit une proposition qu'il donnait à résoudre à tous les mathématiciens de l'Europe ; or, en un endroit de son livre il nommait tous les mathématiciens de l'Europe, et n'en donnait pas un à la France. Il arriva peu de temps après qu'un ambassadeur des États vint trouver le Roi à Fontainebleau. Le Roi prit plaisir à lui en montrer toutes les curiosités, et lui disait les gens excellents qu'il y avait en chaque profession dans son royaume. « Mais, Sire, lui dit l'ambassadeur, vous n'avez point de mathématiciens, car Adrianus Romanus n'en nomme pas un de français dans le catalogue qu'il en fait. -- Si fait, si fait, dit le Roi, j'ai un excellent homme : qu'on m'aille quérir M. Viète. » M. Viète avait suivi le conseil et était à Fontainebleau ; il vient. L'ambassadeur avait envoyé chercher le livre d'Adrianus Romanus. On montre la proposition à M. Viète, qui se met à une des fenêtres de la galerie où ils étaient alors, et avant que le roi en sortît, il écrivit deux solutions avec du crayon. Le soir il en envoya plusieurs à cet ambassadeur, et ajouta qu'il lui en donneroit tant qu'il lui plairait, car c'était une de ces propositions dont les solutions sont infinies^[48] »

En 1595, Viète publie sa réponse au défi d'Adrien Romain, sous le titre Ad problema quod omnibus mathematicis totius orbis construendum proposuit Adrianus Romanus, Francisci Vietae responsum, ou réponse de François Viète au problème qu'a proposé Adrien Romain à tous les mathématiciens du monde.

En publiant ses solutions, Viète s'amuse du professeur de Würzburg :

« Si Adrien Romain n'a pas parcouru tout le globe terrestre, pour croire qu'il n'existe réellement pas sur toute la surface du globe des mathématiciens capables de résoudre son unique problème, au moins n'a-t-il pas compris dans son rayon la France et ses écoles. », écrit Viète dans la réponse qu'il adresse à son rival. « Qu'un Romain l'emporte sur un Belge ou un Belge sur un Romain, soit : mais le Français ne souffrira pas que Belge ou Romain lui enlève la gloire qui lui appartient. Moi qui ne me vante pas d'être mathématicien, mais qui fais seulement de l'étude des mathématiques le délassement de mes loisirs, j'ai résolu le problème d'Adrien en le lisant et sans tomber dans la moindre erreur. Me voilà du coup posé en grand géomètre^[49] ! »

Adrien Romain répond en 1596^{[Notes 8]}. Il écrit^[50] :

« […] un homme éminent, un véritable mathématicien qui ne se laisse pas chatouiller par cet aiguillon de la gloire qui fait perdre la tête à tant d'autres : c'est un Français, nommé François Viète, conseiller du Roi et maître des requêtes au Parlement. Ne pouvant souffrir, comme il dit lui-même, qu'un Belge ou un Romain lui ravit sa gloire, il répondit surabondamment à mon défi par un traité d'une remarquable érudition. »

tout en louant l'unique mais plus précise solution de Van Ceulen (24 décimales contre 9 pour Viète) :

« Le mathématicien français eut sur Ludolphe l'avantage d'assigner toutes les dérivées de l'équation-mère. Cependant à considérer l'exactitude de cette dernière, je dois dire que Ludolphe l'a résolue beaucoup plus complètement que Viète. »

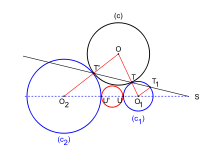
Dans sa réponse de 1595, Viète propose à Romain une autre énigme : la résolution du problème des contacts d’Apollonius de Perge, issu d'un traité qui s'est perdu mais dont la trace des problèmes s'est conservée par Pappus d'Alexandrie^[51]. Adrien Romain affirme l'avoir résolu en aussi peu de temps que Viète a résolu le sien, c'est-à-dire dès réception, et il publie sa solution en 1596 dans le Problema Apollinacum…. Dans la dédicace de l'ouvrage, au bibliothécaire du Vatican, il propose même un arbitrage par des juges italiens : « […] comme nous sommes tous des hommes […], j'ai voulu choisir un juge […] qui ne penchât pour aucune des parties en cause. La lutte étant ouverte entre un Français et un Belge, j'ai récusé tous les juges pris dans ces deux nations, et c'est vous, qui résidez dans cette ville [Rome] où siège le juge suprême de l'univers, c'est vous que j'ai voulu prendre pour arbitre : je vous offre donc ma réponse : examinez-la, et s'il vous convient de vous adjoindre des juges comme Christophe Clavius de la Société de Jésus, Jean Antoine Magin, l'illustre marquis de Monti, ou tels autres que vous voudrez, usez-en à votre discrétion : j'attendrai votre sentence et je m'y soumettrai en toute humilité. »^[52].

Toutefois, la solution de Romain passe par la construction de l'intersection de deux hyperboles^[53], et ne respecte pas les contraintes de construction à la règle et au compas^[54], au contraire de celle que Viète lui communique rapidement par courrier^[55], puis qu'il publie en 1600 dans l'Apollonius gallus^[56], édité en collaboration avec Marino Ghetaldi. Il lui écrit : « Éminent Adrien, tant qu'on touche le cercle par des hyperboles, on ne le touche pas finement. »^{[réf. souhaitée]}.

Avant Tallemant des Réaux^[48], la courtoise dispute entre les deux hommes est narrée par Jacques Auguste de Thou, contemporain de Viète et Romain^[57], mais pas de façon cohérente chronologiquement^[58] : Adrien Romain aurait abandonné Würzburg pour se rendre aussitôt à Paris, puis à Fontenay-le-Comte, où Viète résidait alors dès réception de la solution de Viète à son équation, soit vers 1593, mais à la solution aurait été joint l'Apollonius Gallus paru en 1600 (Viète a cependant envoyé un manuscrit vers 1597). Adrien Romain serait resté six semaines auprès de Viète, qui l'aurait alors initié aux méthodes de l'algèbre nouvelle. Viète aurait fait raccompagner Romain à la frontière et l'aurait même défrayé de ses dépenses. L'épisode est souvent repris au XIX^e siècle et début du XX^e siècle par ses biographes, avec des variantes dans les corrections^[59]. Il semble bien que Romain, venu en France en 1601 pour raisons de santé, ait alors rencontré Viète^[60].

Dans cette double opposition à Viète et à Scaliger, et dans la fidélité permanente de Romain à Clavius, certains auteurs, dont David Rabouin, ont voulu déceler un enjeu allant au-delà de la foi ou de l'orgueil. Selon eux, Romain se veut avant tout fidèle à une certaine conception des mathématiques et de ses fondements, c'est-à-dire sa mathesis. Alors que le pseudo-savant Scaliger croit irréconciliables l'arithmétique et la géométrie et que Viète donne dans son Isagoge (1591) la première piste de cette réconciliation, Romain affirme, dans sa double opposition, l'idée que la mathesis (ou matheseos) n'est pas d'ordre analytique ou algébrique (comme chez Viète), mais « propositionnelle ». Il fait ainsi de la logique le fondement de tout son discours^[61]. Il semble que les écrits de Bosmans relativement au manuscrit de Romain sur l'Algèbre d'Al-Khuwārizmī et les hommages qu'il y rend à l'algèbre figurée (voir paragraphe ci-dessous) tempèrent fortement cette analyse.

En 1598 ou 1599, Adrien Romain rédige et publie en partie un commentaire de l'Algèbre d'Al-Khuwārizmī^{[Notes 9]}. Il n'en reste qu'un fragment — la plupart des manuscrits de Romain ont été détruits en 1914 et en 1944 au cours des bombardements des deux guerres mondiales — mais le bibliothécaire Valerius Andreas en a vu une version complète au XVII^e siècle. Un autre exemplaire, vu à la bibliothèque publique de Douai, apprit à Baldassare Boncompagni que Romain possédait un exemplaire manuscrit du Liber abaci de Fibonacci^[62]. Le R. P. Henri Bosmans a donné une analyse du fragment retrouvé. Il montre qu'Adrien Romain l'a publié en 1598 ou 1599, d'après la liste des œuvres de Viète qu'évoque Romain dans ce fragment. Il affirme à ce propos que Romain est bien informé des œuvres publiées par Viète^[63].

Bosmans montre plus loin que Romain a établi son commentaire d'après la traduction de Robert de Rétines^[64] et classe alors l'algèbre dans les « mathématiques premières », la mathesis. Il y nomme « l'analytique figurée » ce que Viète appelle l'analyse spécieuse^[65] et lui rend un hommage appuyé.

« Il y a, dit Romain, deux manières de traiter l'Analytique : la numéreuse et la figurée. Dans l'Analytique nombreuse, le problème est résolu au moyen des nombres proposés, d'une manière telle, que si aux nombres donnés on en substitue d'autres, il faille recommencer l'opération en entier. Dans l'analytique figurée au contraire, la solution peut s'appliquer à toutes les mises en nombres d'un même problème. »

Dans cet ouvrage, Romain rend également hommage à Guillaume Gosselin, à Nicolas Petri^[66] et à Simon Stevin, puis il ajoute :

« Pour nous, nous avons essayé autrefois d'appliquer la forme figurée à quelques exemples, mais nous l'avons fait d'une manière assez confuse. Viète le premier a employé cette méthode, ainsi qu'on peut le voir dans ses ouvrages et notamment dans ses Zététiques. »

Il conclut sa partie historique en affirmant que personne n'a publié une résolution complète des équations du troisième degré. Mais que trois mathématiciens seulement l'ont trouvé : Viète, van Ceulen et lui. Enfin, dans une dernière partie, il donne des exemples personnels d'algèbre spécieuse, où il se montre le digne successeur du mathématicien français^[67].

L'œuvre scientifique d'Adrien Romain concerne principalement les mathématiques et l'astronomie. Ses notations sont issues de Stevin et de la Coss, mais elles peuvent prendre parfois la forme de la spécieuse^[68]. Lorsqu'il travaille dans le langage de l'algèbre nouvelle, Romain ne marque d'ailleurs que très peu l'homogénéité.

Il ne se trouve pas pour autant de grandes innovations chez Romain. Catholique, élève et ami de Clavius, de Stevin et de Viète, lié à tout ce que l'Europe compte de savants, il demeure généralement dans la continuité des travaux de ses prédécesseurs. Ses calculs du nombre π sont vite oubliés au profit de ceux de van Ceulen ; ni sa trigonométrie, ni ses calculs sur les grands nombres ou les triangles sphériques ne le distinguent de ses contemporains. Il est néanmoins, par le défi qu'il lance aux meilleurs mathématiciens de son temps, par la réponse qu'il en reçoit, par l'hommage qu'il rend alors à la logistique spécieuse, un témoin privilégié et précieux de la transition qui s'opère dans l'écriture algébrique à partir de 1591 ; et, conjuguant l'héritage de Stevin et celui de Viète, il laisse pressentir par ses notations mêlées, les innovations ultérieures d'Albert Girard, ou de Pierre Hérigone.

Romain emploie pour noter l'addition (en 1593) un symbole

« ${\displaystyle \ +\ }$ »

proche d'une croix pattée, ou d'une croix de Malte, qui se trouve également chez De Hortega (1552 et 1563), Guillaume Klebitius (1565) et René Descartes (1637)^[69] ainsi que chez Marino Ghetaldi (1634).

Pour les racines cubiques, il donne l'exposant à l'intérieur de la racine, sous la barre horizontale, c'est-à-dire sous le vinculum (Albert Girard^[70] note pour la première fois vers 1625 un exposant extérieur sous la forme moderne).

Enfin, Adrien Romain emploie également la notation « R.bin » pour la racine carrée, notant par exemple, comme Viète^[71] :

${\displaystyle R.bin.2+R.bin.2+R.bin.2+R2}$

pour

${\displaystyle {\sqrt {2+{\sqrt {2+{\sqrt {2+{\sqrt {2}}}}}}}}}$.

Un cours d'Adrien Romain, datant de 1596 et portant sur les calculs des grands nombres est parvenu à la postérité grâce aux notes d'un de ses élèves, le père Jacques Nivelle, de la Compagnie de Jésus^[2]. Cet ouvrage manuscrit, De multiplicandi, dividendi, quadrata componendi, évoquant la multiplication, la division et la formation des carrés, est un manuel de calculs des grands nombres. Sur le même thème, Romain publie en 1607 un Methodus experimendi numeros, aujourd'hui perdu. On y trouve exposé en quelques pages des méthodes originales pour élever au cube ou extraire des racines carrées.

En 1593, dans son traité sur les polygones, puis en 1597 dans son traité intitulé in Archimedis, circuli dimensionem expositio et analysis^[72], Romain publie les 16 premières décimales de π. Il pousse le procédé d'approximation polygonale employé par Archimède jusqu'à exprimer le périmètre de polygones inscrits et circonscrits ayant ${\displaystyle 2^{30}}$ côtés^[73],[74]. Son intérêt passionné pour le nombre π n'avait d'égal que celui de son ami van Ceulen.

Ludolph van Ceulen en publie pour sa part 20 décimales dans son livre Van den Circkel^[75] (Sur le cercle) en 1596, puis 35 décimales entre 1603 et 1610 (pour un polygone régulier de ${\displaystyle 60.2^{33}}$ côtés). Son élève Willebrord Snell publie ces résultats en 1619^[76].

Dans son ouvrage intitulé Chordarum arcubus circuli primarilis, quibus videlicet is in triginta dirimitur partes, subtensarum resolutio (1602, de la corde des arcs de cercle découpé de façon évidente en trente parties, et de leur résolution), il calcule les racines de plusieurs équations algébriques qui lui servent à exprimer la longueur des côtés de plusieurs polygones réguliers (le titre l'indique : son objet principal est le polygone régulier de 30 côtés) et lui permettent de dresser des tables de sinus. Dans sa préface, se trouvent quelques détails sur les déboires que subit Adrien Romain de la part des imprimeurs et des ouvriers typographes, rebutés et découragés par les difficultés de l'impression de son livre (la même mésaventure est arrivée à Viète lors de l'impression de son Canon en 1579)^[77]

L'ouvrage lui-même est divisé en huit parties. Adrien Romain caresse l'ambition de publier des tables trigonométriques à 9 décimales. Jusque-là, les astronomes utilisent les tables trigonométriques à 10 décimales de Rheticus, publiées en 1596 par son étudiant Valentin Otho dans l'Opus palatinum de triangulis^[78]. Romain doute de l'exactitude de ces tables : dans une lettre adressée à Clavius, le professeur du Collège romain à Rome, il observe que pour dresser une table des tangentes et des sécantes précises à 10 décimales près, il faut préalablement disposer de tables de sinus à 20 décimales^[79].

À cette fin, il développe le calcul de certaines racines carrées à plus de deux cents décimales exactes. Ces calculs sont probablement les plus anciens qui aient été imprimés. Ainsi, dans le Chordarum arcubus circuli, donne-t-il sous forme de lemmes, les valeurs approchées, avec 218 décimales, de^[2] :

${\displaystyle {\sqrt {3}};\ \ {\sqrt {5}};\ \ {\sqrt {15}};\ \ {\sqrt {10\pm {\sqrt {20}}}};\ \ {\sqrt {30\pm {\sqrt {180}}}}}$

D'autres écrits mathématiques d'Adrien Romain concernent les rapports entre polygones de même périmètre. Pappus d'Alexandrie a déjà établi de nombreux résultats concernant la superficie maximum des polygones de périmètre donné. Ainsi, il a montré que, de tous les polygones de même périmètre, le polygone régulier possède la superficie maximum. Romain généralise ce résultat.

En 1606, Romain publie un « miroir astronomique », Speculum astronomicum, sive, organum forma mappae expressum^[80]. Ce livre serait le premier traité de trigonométrie faisant un emploi systématique de notations abrégées comme sin(A+B) et la plus vieille trace d'algébrisation du calcul trigonométrique selon Bosmans^[6]. En général, celle-ci est plutôt attribuée à Albert Girard dans sa traduction du Marolois^[81].

En 1609, Romain publie un Canon triangulorum sphaericorum, brevissimus simul ac facilimus quam plurimisque exemplis optice projectis illustratus, in gratiam astronomiae, cosmographiae, geographiae, horologiographiae, etc., studiosorum jam primum editus^[82] où, effrayé par l'horrible prolixité de Rheticus et d'Otho, il réduit toute la trigonométrie sphérique à six problèmes^[83].

Dans ce traité, Romain donne ces lignes trigonométriques sous forme de tableaux, avec neuf et seize décimales, ainsi que certaines expressions analytiques des sinus, des sécantes et des tangentes. On y retrouve l'emploi de la prostaphérèse^{[Notes 10]}. Dans la partie consacrée aux (six) formules de base des triangles sphériques, il rend hommage aux mathématiciens qui l'ont précédé parmi lesquels Viète, Clavius, Mangin, Lansberg, Fincke et Pitiscus. Jean-Baptiste Delambre note qu'en dépit des simplifications annoncées, Adrien Romain n'a pu véritablement tenir ses promesses initiales et donner un traité plus lisible que celui de Rhéticus. Il en veut pour témoignage les quatre vers latins concluant le traité et censés faciliter la mémorisation des formules^[84] :

« Spes turbida cessit ;
Plurima se (ad)tollant superi praesente periclo ;
Sevitie si sors stimulet suspiria sursum ;
Saepe tibi tutam poterunt praestare salutem. »

En tant qu'astrologue et spécialiste du comput, il publie en 1594 sa Theoria calendariorum, un livre dans lequel il donne le calendrier liturgique pour les années 1596-1603, ainsi que l'annonce des éclipses de la Lune et du Soleil. Défendue par un de ses élèves, un jeune chanoine de Posen du nom d'Adam Swinawski, leur première production est dédiée au prince Jules Echter^{[Notes 11]}. Il semble que l'intérêt d'Adrien Romain pour les calendriers ne soit pas que l'effet de commandes liées à son prince ou à sa communauté religieuse mais trouve son origine dans les querelles qui l'ont opposé à Scaliger sur la réforme du calendrier grégorien^[85].

Adrien Romain se distingue également par l'évolution qu'il apporte aux études médicales. Néanmoins il ne publie pas de livre de médecine et seules les thèses soutenues par ses élèves témoignent de ses avancées, notamment le De Formatione Fœtus liber in quo ostenditur animam rationalem infundi tertia die de Thomas Fyens (ou Fienus). Ce qu'écrit sous sa direction Thomas Fyens à propos de la formation du corps humain dans l'utérus résume l'essentiel des connaissances de l'époque. Les auteurs se préoccupent alors de déterminer l'époque où « l'âme » se manifeste dans le fœtus. Fyens prétend quant à lui que les affections morales de la mère se transmettent à son enfant au travers de ses facultés nutritives^[86].

Henri Bosmans a publié une liste analytique de ces ouvrages dans la Bibliographie Nationale de l'Académie Royale des Sciences de Belgique, t. XIX, p. 848–889. Le nom d'Adrien Romain se retrouve dans de nombreuses publications et quelques manuscrits non édités. Au milieu du XIX^e siècle, Ruland en recense soixante^[1]. Pour une part d'entre elles, il s'agit de dissertations d'élèves, principalement des étudiants en médecine, qu'il a examinées lors de leur magistère. Toutes ces œuvres sont en latin. Quelques-unes des plus remarquables sont indiquées ci-dessous, avec un bref rappel de leur contenu ; aucune de ces œuvres n'a été publiquement traduite du latin.

• L'Ouranographie : Ouranographia sive cæli descriptio : in qua præter alia, cælorum numerus & ordo methodo inquiruntur, omniaq́ue ea quæ ad primum cælum, primumq́ue mobile ab eo distinctum spectant, dilucidè explicantur, nominibusq́ue aptè fictis distinguuntur^[87], imprimé chez Ioannis Masij, Louvain, 1591.
  Divisée en trois livres, l'ouranographie de Romain discute en particulier de la nature et du nombre des sphères célestes^[3] (le système est celui de Ptolémée).
• Les Idées mathématiques : Ideae mathematicae pars prima, sive methodus polygonorum ; qua laterum, perimetrorum & arearum cujuscunq́ue polygoni investigandorum ratio exactissima & certissima; unà cum circuli quadratura continentur, imprimé par Ioannem Keerbergium, 1593 à Anvers^[88]
  Dédicacé à Christopher Clavius, cet ouvrage comporte également des vers de Juste Lipse et de Thomas Fienus (ou Feyens, son élève). C'est dans cet écrit qu'est lancé le défi aux meilleurs mathématiciens de son temps ainsi que les quinze décimales de π.
• Le Théâtre du monde : Parvum theatrum urbium praecipuarum totius orbis brevis et methodica descriptio, ex officina typographica Nicolai Bassæi, 1595.
  Cette description des villes européennes au XVI^e siècle doit en réalité assez peu à Romain, c'est une compilation de travaux de Georg Braun, ainsi qu'annoncé en avant propos, présentée dans un ordre géographique plutôt qu'alphabétique comme dans l'original. Il est illustré de petites gravures sur bois que l'éditeur utilise également dans d'autres publications^[89].
• La collection météorologique : Ventorum sec. recentiores dictinctorum usus, Würzburg, 1596^[90].
  Recension de centaines de thèses sur la rose des vents, la prévision du temps et autres thèmes de physique sur l'effet mécanique des vents. L'originalité en est une classification des vents selon leur direction.
• La Réponse à Viète : Problema Apollinacum quo datis Aribus circulis quaeritur quartus eos contingens, antea ab illustri viro D. Francisco Vieta ... omnibus mathematicis sed potissimum Belgii ad construendum propositum jam vero^[91], imprimé par G. Fleischmann, Wircebvrg, Würzburg, 1596.
  C'est dans cet opuscule que Romain donne sa construction par hyperbole du quatrième cercle tangent. Henri Bosmans accrédite l'idée que Romain cherche ultérieurement à faire disparaître les exemplaires en circulation de cet ouvrage^[6]. Il en demeure 4 exemplaires au monde.
• Sur Archimède : in Archimedis circuli dimensionem expositio et analysis ; Apologia pro Archimede ad [… J.] Scaligerum^[72], publié avec Exercitationes Cyclicæ contra J. Scaligerum, O. Finæum et R. Ursum, in decem dialogos distinctæ, imprimé à Genève, 1597, mais indiqué comme étant imprimé à Wurzbourg.
  Dans ce livre, divisé en trois parties, Romain redonne les 16 décimales du nombre de Ludolph ; le suivent deux autres traités, dirigés contre Scaliger et les faux quadrateurs.
• Contre Scaliger : Exercitationes cyclicae contra Josephum Scaligerum, Orontium Finaeum et Raymarum Ursum^[92] (Contre Scaliger et ses prétentions cyclométriques), publié à Würzburg, 1597, par Adriano Romano avec Apologia pro Archimede^[93].
• Theses Astronomicae : Quibus proponuntur nonnulla de corporum mundanorum simplicium distinctione et numero, iuxta tum veterum tum recentiorum benè philosophantium sententiam, relictis interim cænophilorum nonnullorum opinionibus : prætereà, specimen constructionis magnæ chordarum tabulæ ... ; quæ quidem omnia die Sabbathi proximo qui est 18. Julij, hora octava antemeridiana, in Schola Medica^[94], imprimé à Würzburg, Fleischmann, 1598, en collaboration avec Lambertus Croppet.
  Contre les amateurs de nouveautés dans une première partie, le livre illustre dans une seconde partie des méthodes de travail avec les grands nombres.
• Calculs de cordes : Resolutionis chordarum arcubus circuli primariis subtensarum pars secunda et tertia: quibus usus geneseon et analyseos præcedenti libro propositarum uberrimus continetur^[95], imprimé par Georgius Fleischmann, 1602.
  Cité par Fermat^{[réf. souhaitée]} ; Romain y donne √5 avec 300 décimales.
• Mathématiques de guerre : Mathesis polemica^[96], sumptibus Læuini Hulsij Gandensis, Francfort, 1605.
  Ouvrage divisé en trois parties, en premier lieu une énumération des branches des mathématiques, suivie d'un exposé de sa méthode pour calculer la distance entre deux points inaccessibles ; enfin, dans une troisième partie, Romain donne en sept chapitres les applications des mathématiques à l'art de la guerre.
• Le Miroir astronomique : Speculum astronomicum, sive organum forma mappae expressum ; in quo licet immobili omnes qui in primo caelo, primoque mobili spectari solent motus, per canones ea de re conscriptos, planissime sine ullius regulae aut volvelli beneficio repraesentantur^[97], imprimé par Joannis Masius, 1606.
  Cet ouvrage dédié à l'Archiduc Albert se compose de deux livres, dont l'un de trigonométrie sphérique. Romain y fait usage d'une symbolique algébrique plus proche de Marule que de l'algèbre nouvelle. Si dans cet ouvrage il se montre influencé par l'Apollonius gallus, c'est plus par son Canon que par son Isagoge. Il s'y trouverait une notation donnant ${\displaystyle \sin(A+B)}$.
• Le canon de Romain : Adriani Romani canon triangulorvm sphæricorum: brevissimus simul ac facilimus quam plurimisq; exemplis opticè proiectis illustratus, in gratiam astronomiæ, cosmographiæ, geographiæ, horologiographiæ, &c studiosorum iam primùm editus. Accessere plenioris usus ergo^[98], imprimé par Joannis Albini, 1609, introduction de Christophe Clavius.
  Une première publication a eu lieu en 1593. Le livre est censé reprendre les connaissances de son temps, notamment celles données en 1579 par François Viète dans son propre canon^[6].
• Des feux d'artifice : Pyrotechnia, hoc est, De ignibvs festivis, iocosis, artificialibvs et seriis, variisqve eorum structuris, libri dvo. Ex scriptoribus latinis, italis, et germanis collecti, & in methodum succinctam redacti. In gratiam eorum, qui hisce artibus iucundi spectaculi caussa delectantu^[99], Prostat in Officina Paltheniana, Francfort, 1611.
  Ce traité sur la formation des feux d'artifice est singulier pour l'époque à laquelle il a été écrit, note Henri Bosmans.
• Sa correspondance, formée de lettres à Scaliger, à Juste Lipse, au prince Julien, à l'astronome Mangin, et à Kepler.
• Une thèse : De disputatio medica et physica. De elementis, imprimée par Georgium Fleischmann, Würzburg, 1594, et dédiée à Henning Scheunemann.

Quelques mémoires d'Adrien Romain (thèses d'élèves)

• examen de Propositiones de semine sanguineque materno, typis Georgii Fleischmanni, thèse de son élève Johann Birenstill, 1595.
• examen de Theses medicae de febre putrida et febre pestilentiali, pro primo medicinae gradu acquirendo defendere conabitur, thèse de Jean Faber, édité chez Georgius Fleischmann, en 1597.
• examen de Osteologia humana sive de scheleto quod totius anatomes praecipuum fundamentum & basis existit assertiones, imprimé par Georgii Fleischmanni, 1599 Würzburg, thèse de Johannes Fuchs, un des élèves d'Adrien Romain.
• examen de Disceptatio anatomica de partibus thoracis earumque convenienti administrandi ratione, imprimé par Georgii Fleischmanni, 1602 à Würzburg, thèse de Kaspar Fridericus.
• examen de Disputatio anatomica de partibus corporis nutritioni dicatis : earumque administrandi ratione, imprimé par Georgii Fleischmanni, Würzburg, 1603, thèse de Johann Konrad Burckhard de Rothenburg^[100].

• D'Adrien Romain également, une Disputatio theologica secunda de scientia dei^[101], imprimée chez Ioannes Patius, à Lyon, 1615, soutenue devant Simon Episcopius^[102].
• Et enfin, dédicacé par Snell : le Petri Rami veromandui professoris regii geometriae libri XXVII, imprimé par Guilielmus Antonius, Hanau, 1604, sur la géométrie de Pierre de La Ramée par Willebrord Snell.

Le Tractatus de formatione corporis humani in utero lui a parfois été attribué^[103] à tort : il est en réalité dû à Ægidius Romanus^[104].

• In Mahumedis arabis, Algebram prolegomena : il s'agit d'un commentaire d'Adrien Romain sur l'Algèbre de Mahumed ben Musa Al-Khuwārizmī^[105]. Il ne fut imprimé qu'en partie et il n'en reste qu'un fragment.
• Tractatus de notatione numerorum : explication de divers symboles de numération.
• Nova multiplicandi, dividendi, quadrata componendi, radiées extrahendi ratio, multo quam pervulgata certior, facilior, et majoribus maxime numeris accommodatior : traité de calculs numériques.

Les travaux d'Adrien Romain sont connus de Pierre de Fermat, qui s'en inspire et communique à Huygens ses propres solutions au défi de Romain vers 1661^[106]. Plus tard, Montucla retrouve la trace du mathématicien flamand au travers de ses débats avec Viète. En 1796, Kastner, de Göttingen, étudie un de ses manuscrits ; mais au commencement du XIX^e siècle, seules sont vraiment connues ses publications de médecin et les thèses, déjà très datées, que soutenaient ses élèves^[86].

Seuls Jean-Baptiste Delambre puis Michel Chasles vont plus loin, le premier en analysant sa trigonométrie sphérique^[79] et le second quand il écrit de lui et de l'analyse de Romain^[107] :

« Il semble donc que c’est Romanus qui a le plus approché de la conception de Viète, dans ce sens qu’il en a eu l’idée ; mais il n’a pas su appliquer cette idée heureuse... Néanmoins la tentative de Romanus lui fait honneur et rehausse le mérite et la gloire de Viète, car Romanus était lui-même un homme de génie et un très habile et très célèbre géomètre. C’est à tort, je crois, que l’on avait passé sous silence jusqu’ici, dans l’histoire des Mathématiques, sa conception analytique que nous venons de rappeler. »

Néanmoins, la renaissance des études sur Adrien Romain est liée aux travaux du baron de Reiffenberg^[2],[27], puis aux études du professeur Louis-Philippe Gilbert^{[Notes 12]} de l'université de Louvain.

Cette renaissance se poursuit par une étude sans précédent, publiée dans les trois ans qui suivent par Anton Ruland^[1], qui exhume son important travail dans le domaine de la médecine^[2].

Enfin, de 1900 à 1907, tandis que Charles Henry le débusque dans une lettre de Fermat^[106], et que Bierens de Haan^[2] en donne des traductions, l'immense travail du père Henri Bosmans, publié dans les Annales de la société scientifique de Bruxelles, Bibliotheca Mathematica ou la Biographie nationale, ainsi que, sous le pseudonyme de H. Braid, dans L'Intermédiaire des mathématiciens^[108], permet de retrouver sous sa plume la figure oubliée du mathématicien de Würzburg^[107].

Plus récemment, d'autres érudits ont participé à cette tâche, dont Jean Itard et Roshdi Rashed. Adrien Romain ou Roomen a fait l'objet de plusieurs articles de P. Bockstaele dont l'un tente de mieux cerner son apport entre Viète et Descartes^[109].

• Philippe Gilbert, « Notice sur le mathématicien louvaniste Adrianus Romanus, professeur à l'ancienne Université de Louvain (XVI^e siècle) », Revue catholique, vol. XVII,‎ 1859, p. 277-286, 394-409 et 522-527 (lire en ligne).
• Anton Ruland, « Adrien Romanus, premier professeur à la faculté de médecine de Wurzbourg », Le Bibliophile belge, Bruxelles, Fr. J. Olivier, vol. 2,‎ 1867, p. 56-100, 161-187 et 256-269 (lire en ligne) (p. 56 : notice biographique, p. 161 et 256 : liste chronologique des éditions des ouvrages de Romain connues de l'auteur).
• Henri Bosmans, « Romain (Adrien) », dans Biographie nationale, vol. 19, 1907 (lire en ligne), p. 848-889 (disponible sur le site de l'université de Gand).
• Quido Vetter, « Sur L'équation du quarante-cinquième degré d'Adriaan van Roomen », Bulletin des sciences mathématiques, vol. LXV,‎ 1930, p. 277-283 (lire en ligne)
• (nl) Paul Bockstaele, « Roomen, Adriaan van (1561-1615) », dans Nationaal biografisch woordenboek, Bruxelles, 1966 (lire en ligne), p. 751-765.
• (en) Paul Bockstaele, « The correspondence of Adriaan van Roomen », LIAS, vol. 3,‎ 1976, p. 85-129 et 245-299 (lire en ligne).
• (en) Paul P. Bockstaele, The correspondence of Adriaan van Roomen, KU Leuven, Departement Wiskunde, 1979 (OCLC 220195899).
• (en) Paul Bockstaele, « The correspondence of Adriaan van Roomen (1561-1615), corrections and additions, 1594-1615 », LIAS, vol. 19,‎ 1992, p. 3-20 (lire en ligne).
• (en) H. L. L. Busard, « Roomen, Adriaan Van. », dans Complete Dictionary of Scientific Biography, Détroit, éditions Scribner, 2008 (ISBN 978-0-684-31559-1, lire en ligne).

• (en) John J. O'Connor et Edmund F. Robertson, « Adriaan van Roomen », sur MacTutor, université de St Andrews. — Un portrait de Jules César Scaliger y est présenté par erreur.
• Notices d'autorité :

  • VIAF
  • ISNI
  • BnF (données)
  • IdRef
  • LCCN
  • GND
  • Italie
  • Espagne
  • Belgique
  • Pays-Bas
  • Pologne
  • NUKAT
  • Suède
  • Vatican
  • Tchéquie
  • Portugal
  • WorldCat
• Notices dans des dictionnaires ou encyclopédies généralistes :

  • Biografisch Portaal van Nederland
  • Deutsche Biographie
  • Enciclopedia De Agostini

• Portail du Brabant flamand
• Portail des mathématiques
• Portail algèbre nouvelle et François Viète