Angle inscrit dans un demi-cercle — Wikipédia
Le théorème de géométrie qui affirme que l'angle inscrit dans un demi-cercle est droit, est appelé théorème de Thalès en Allemagne (Satz des Thales) à partir de la toute fin du XIXe siècle, puis dans plusieurs pays, mais assez rarement en France où, à partir à peu près de la même époque, le « théorème de Thalès » désigne un théorème tout autre, sur la proportionnalité des segments découpés sur deux droites sécantes par des droites parallèles.
Plus précisément le théorème affirme que si un point d'un cercle est le sommet d'un angle qui recoupe le cercle en deux points diamétralement opposés, alors cet angle est un angle droit. Un autre énoncé, immédiatement équivalent, est qu'un triangle inscrit dans un cercle et dont un côté est un diamètre est un triangle rectangle. C'est un cas particulier du théorème qui lie l'angle inscrit à l'angle au centre, l'angle droit étant la moitié de l'angle plat. La réciproque est la propriété du triangle rectangle inscrit dans un cercle qui affirme qu'un triangle rectangle est inscrit dans un cercle dont un diamètre est l'hypoténuse de ce triangle.
Le théorème (le sens direct) est démontré dans le livre III des Éléments d'Euclide (~ 300 av. J.-C.), à la proposition 31, mais sa démonstration, citée par Aristote, fait manifestement déjà partie de la culture mathématique grecque à l'époque du Stagyrite. Son attribution à Thalès de Milet (autour de 600 av. J.-C.) repose sur un écrit de Diogène Laërce (IIIe siècle apr. J.-C.), qui relate une tradition attribuant le théorème soit à Thalès soit à Pythagore.
Le théorème
[modifier | modifier le code]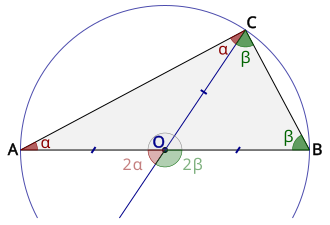
2α + 2β égale l'angle plat, donc α + β égale l'angle droit.
Un énoncé possible du théorème est le suivant :
Si un triangle ABC est inscrit dans un cercle de diamètre [AB], c'est-à-dire que le point C appartient également à ce cercle, alors le triangle est rectangle en C.
Une démonstration s'appuie d'une part sur une propriété des triangles isocèles, à savoir que si deux côtés sont de même longueurs, deux angles sont de même mesure, d'autre part sur la propriété que la somme des angles d'un triangle égale l'angle plat.
En effet, soit O le milieu de A et B, comme O est centre du cercle de diamètre [AB] passant par C, les triangles OAC et OBC sont isocèles de sommet O, d'où les égalités d'angles suivantes :
- .
Le triangle ABC a pour angle en A l'angle en A du triangle OAC, en B celui du triangle OBC, et en C un angle qui vaut la somme des angles en C de ces triangles, soit
c'est-à-dire que l'angle en C du triangle ABC vaut la somme des deux autres angles de ce triangle :
et comme la somme des angles du triangle ABC est l'angle plat, l'angle en C vaut la moitié c'est-à-dire l'angle droit, c'est-à-dire que le triangle est rectangle en C.
Une variante de la démonstration (esquissée sur le schéma ci-dessus) utilise le résultat sur la somme des angles pour les triangles OAC et OBC.
Réciproque
[modifier | modifier le code]
On a également la réciproque de ce théorème :
Si ABC est un triangle rectangle en C alors le triangle s'inscrit dans un cercle de diamètre l'hypoténuse [AB].
C'est un corollaire du sens direct par une méthode de fausse position. En effet supposons que le triangle ABC n'est pas inscrit dans le cercle de diamètre [AB]. La seconde intersection de la droite (AC) et du cercle de diamètre [AB] est un point C' distinct de C par hypothèse. La droite (AC) n'est donc pas perpendiculaire à (BC), c'est-à-dire que le triangle ABC n'est pas rectangle, ce qui est la contraposée de la réciproque.

On peut aussi démontrer directement la réciproque, par exemple en utilisant les propriétés de la droite des milieux : la droite passant par le milieu O du segment [AB] et le milieu I du segment [AC] est parallèle à la droite (BC). Comme les droites (AC) et (BC) sont perpendiculaires, il en est de même des droites (AC) et (OI). La droite (OI) passe par le milieu de [AC], est perpendiculaire à (AC), c'est donc la médiatrice de A et C, d'où OA = OC. Finalement O, étant milieu de A et B, OA = OC = OB : le point O est le centre du cercle circonscrit au triangle, qui a pour diamètre [AB].
Le triangle rectangle peut aussi être complété en un rectangle dont la diagonale [AB] est l'hypoténuse du triangle. Les diagonales du rectangle sont de même longueur et se coupent en leur milieu d'où le résultat.
Le sens direct peut également se déduire de la réciproque par fausse position.
Du théorème et de sa réciproque, on déduit que le lieu des points d'où un segment [AB] est vu sous un angle droit est le cercle de diamètre ce segment [AB]. Dit autrement le lieu des points qui sont le sommet de l'angle droit d'un triangle rectangle d'hypoténuse un segment donné [AB] est le cercle de diamètre [AB].
Histoire
[modifier | modifier le code]Euclide
[modifier | modifier le code]La proposition 31 du livre III d'Euclide traite trois cas : l'angle inscrit dans un demi-cercle, l'angle inscrit dans un segment de cercle (l'une des deux parties du cercle délimitée par une corde) plus grand qu'un demi-cercle, et l'angle inscrit dans un segment de cercle plus petit qu'un demi-cercle. La conclusion est que dans le premier cas l'angle est droit, ce qui est le théorème traité ici, dans le second qu'il est inférieur à l'angle droit, et dans le troisième cas qu'il est supérieur au droit. La proposition prolonge le résultat pour les angles curvilignes (entre la corde et le cercle).
Les démonstrations reposent sur celle du premier cas : l'angle inscrit dans un demi-cercle. Celle-ci est en gros celle exposée ci-dessus. Euclide matérialise l'angle plat double de l'angle dont il montre qu'il est droit en prolongeant au-delà du sommet l'un des côtés de cet angle (l'angle en C pour le schéma ci-dessus). Euclide s'appuie sur les propositions 5 (sur les triangles isocèles), 32 (sur la somme des angles d'un triangle) et sur la définition 10 (sur l'angle droit) du livre I[1]. La variante citée ci-dessus apparaît dans certaines éditions anciennes[2].
Avant Euclide
[modifier | modifier le code]Le théorème ne date manifestement pas d'Euclide, Aristote le cite à deux reprises et décrit une démonstration analogue à celle d'Euclide[3].
Selon Diogène Laërce « Pamphila raconte, de son côté, qu’il [Thalès] avait appris la géométrie des Égyptiens ; que le premier il inscrivit dans le cercle un triangle rectangle, et qu’il immola un bœuf à cette occasion. Apollodore le calculateur et quelques autres mettent cela sur le compte de Pythagore »[4]. Le texte grec est ambigu et peut être également traduit par « il inscrivit dans une partie du cercle un triangle rectangle », ou « il inscrivit dans une partie du cercle un triangle dont il était requis qu'il fût rectangle »[5]. On a la réciproque du théorème pour les deux premières traductions, le sens direct pour la dernière[5].
La démonstration du sens direct que l'on trouve dans Aristote (et dans Euclide) utilise deux propriétés du livre I des Éléments :
- celle concernant l'égalité des angles dans un triangle isocèle est attribuée par Proclus à Thalès de Milet[6],
- celle concernant la somme des angles du triangle est attribuée par Proclus à l'école pythagoricienne[5],
ce qui peut expliquer l'attribution du théorème à l'un ou l'autre des philosophes.
Même s'il peut être contesté, Proclus est considéré plus fiable par les historiens de l'antiquité que Diogène Laërce[5], car son commentaire sur le livre I semble suivre d'assez près une histoire (disparue) d'un élève d'Aristote, Eudème de Rhodes. Mais le résumé d'Eudème par Proclus ne concerne que le livre I, et il ne cite donc pas la propriété de l'angle inscrit dans un demi-cercle.
La démonstration d'Euclide (du sens direct) demande, si ce n'est de connaître la mesure des angles, de savoir les additionner, ce qui paraît difficilement accessible à Thalès. Cependant la réciproque, par la propriété de l'intersection des diagonales des rectangles n'utilise que des « égalités » d'angle, que l'on estime selon Eudème (cité par Proclus) accessibles à Thalès, et il est possible également de donner une démonstration du sens direct n'utilisant que ces propriétés[7].
Il reste que la pratique des mathématiques de l'époque de Thalès ne peut être que très différente de celle de l'époque d'Euclide et même d'Aristote. Les énoncés de Thalès et de l'école Ionienne et leurs relations pourraient bien relever plutôt de l'intuition empirique que de la démonstration logique, malgré l'avis contraire du mathématicien et historien des mathématiques Bartel van der Waerden, qui paraît là dessus assez isolé[8].
Appellation
[modifier | modifier le code]L'éducation secondaire se démocratise au cours du XIXe siècle. La géométrie, qui a souvent pour but d'exercer à la logique, en est un élément important. Les manuels se répandent, et leurs auteurs se mettent à introduire plus ou moins systématiquement des éléments historiques, en particulier en attribuant des noms de mathématicien aux théorèmes. L'époque est également au renouveau des recherches historiques sur les mathématiques de la Grèce antique. C'est dans ce contexte qu'à partir de la fin du XIXe siècle le nom de Thalès est attribué à deux théorèmes distincts. En France puis en Italie c'est à un théorème du livre VI des Éléments d'Euclide, soit celui sur la proportionnalité des segments découpés par une ligne parallèle à un côté dans un triangle, soit sa généralisation pour deux sécantes (voir théorème de Thalès). En Allemagne c'est au théorème de l'angle inscrit dans un demi-cercle. Ces dénominations sont bien établies dans les années 1920, époque à laquelle d'autres pays adoptent l'une ou l'autre (mais pas l'Angleterre ni les États-Unis)[9].
Ces choix correspondent à des traditions différentes d'enseignement de la géométrie, plutôt fidèle à Euclide et à l'ordre d'exposition des Éléments en Allemagne, alors qu'une tradition plus anti-euclidienne s'est développée en France depuis La Ramée. Le choix s'est porté en France et en Italie, sur un théorème qui met en évidence un invariant de la géométrie affine, le rapport de mesures algébriques sur une droite, ce qui correspond au développement en Europe de la géométrie projective et affine au XIXe siècle. Ce théorème est mis en avant dans les débuts de l'apprentissage de la géométrie, alors que l'Allemagne privilégie le théorème de Pythagore, et choisit de donner le nom de Thalès à un théorème lié au triangle rectangle[10].
Dans un cas comme dans l'autre, le choix du nom n'a finalement pas obéi a des considérations strictement historiques[11]. L'histoire est instrumentalisée au service d'un choix didactique : il s'agit de mettre un théorème en avant, en lui attribuant le nom d'un mathématicien célèbre, d'où des choix différents dans des traditions d'enseignement différentes[12].
Notes et références
[modifier | modifier le code]- Vitrac
- Comme les éditions de Peyrard, voir bibliographie.
- dans les Analytiques postérieurs, II, 11, 94a28, et la Métaphysique, 1051a26 selon Caveing 1997, p. 53.
- Traduction de Charles Zévort XIXe siècle, lire en ligne sur le site remacle.org.
- Caveing 1997, p. 53.
- Caveing 1997, p. 34.
- Caveing 1997, p. 56-57.
- Caveing 1997, p. 74-75
- Patronis et Patsopoulos 2006, p. 60-61.
- Patronis et Patsopoulos 2006, p. 62-63.
- L'appellation du théorème a d'ailleurs été critiquée, voire rejetée, par les historiens au moment de son apparition (Patronis et Patsopoulos 2006, p. 60).
- Selon Patronis et Patsopoulos 2006, p. 63-64.
Bibliographie
[modifier | modifier le code]- Maurice Caveing, La figure et le nombre : recherches sur les premières mathématiques des Grecs, vol. 2, Presses universitaires Septentrion, , 424 p. (ISBN 978-2-85939-494-3)
- (en) T. Patronis et D. Patsopoulos, « The Theorem of Thales: A Study of the naming of theorems in school Geometry textbooks », The International Journal for the History of Mathematics Education, vol. 1, no 1, , p. 57-68 (lire en ligne)
- Euclide (trad. Bernard Vitrac), Les Éléments [détail des éditions] Volume 1, proposition 31 livre III, p. 449-450
- Les élémens de géométrie d'Euclide , traduits littéralement et suivis d'un Traité du cercle, du cylindre, du cône et de la sphère, de la mesure des surfaces et des solides, avec des notes, par F. Peyrard, F. Louis (Paris), (lire en ligne), p. 161-163, figure 94 (sur gallica), voir aussi cette version numérisée (remacle.org).


 French
French Deutsch
Deutsch

