Cube de Necker — Wikipédia
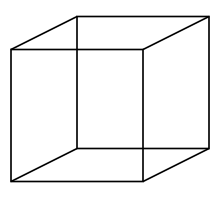
Le cube de Necker est une image ambigüe provoquant une illusion d'optique, mentionnée pour la première fois avec un dessin en perspective cavalière d'un rhomboïde en 1832 par le cristallographe suisse Louis-Albert Necker[1].
Ambiguïté
[modifier | modifier le code]Le cube de Necker est un dessin ambigu. C'est un dessin des arêtes d'un cube en perspective cavalière, ce qui signifie que les bords parallèles du cube sont dessinés avec des lignes parallèles sur le dessin. Quand deux lignes se croisent, le dessin ne montre pas laquelle est devant et laquelle est derrière. Ceci rend le dessin ambigu ; il peut être interprété de deux manières différentes. Quand une personne observe le dessin, elle remarquera alternativement chacune des deux interprétations valides (c'est une perception multistable (en)).

L'effet est intéressant, car chaque partie de dessin est elle-même ambiguë, l'œil humain fait alors une interprétation individuelle de chaque partie qui rend le tout homogène. Le cube de Necker est souvent utilisé pour tester les modèles informatiques du système visuel humain pour voir s'ils parviennent à une interprétation de l'image similaire à celle d'un humain.
L'homme ne parvient pas en général à une interprétation irrationnelle du cube. Un cube dont les arêtes se croisent de manière incohérente est appelé un objet impossible, plus spécifiquement un cube impossible.
Sur le cube de gauche, la plupart des gens voient la partie en bas à gauche comme étant en avant. Cela vient probablement du fait que les gens perçoivent les objets par-dessus, avec la face haute visible, beaucoup plus souvent que par-dessous, avec la face basse visible. Le cerveau « préfère » alors l'interprétation du cube vu de haut.
Il y a des preuves qu'une concentration plus prononcée sur des parties différentes de la figure peut mener à une visualisation plus stable du cube. L'intersection des deux faces parallèles à l'observateur forme un rectangle, et les lignes qui se croisent au niveau du carré forment une intersection en Y aux deux côtés opposés. Si un observateur se concentre sur l'intersection en Y du haut, la face en bas à gauche apparaîtra en avant. La face en haut à droite apparaîtra en surimpression si l'observateur se concentre sur l'intersection en Y du bas (Einhauser, et al., 2004).
Théorie de la connaissance
[modifier | modifier le code]Le cube de Necker est utilisé en théorie de la connaissance et permet de contre-attaquer le réalisme naïf, concept qui veut que le monde soit tel que nous le percevons.
Le cube de Necker semble démonter cette théorie : nous voyons un cube, mais en réalité il n'y a pas de cube du tout, juste une figure à 2 dimensions de 12 lignes. Nous voyons quelque chose qui n'est pas vraiment là, ce qui désapprouverait le réalisme naïf. Cette critique du réalisme naïf soutient la thèse du réalisme représentatif.
Notes et références
[modifier | modifier le code]- Louis Albert Necker, Observations on some remarkable optical phaenomena seen in Switzerland; and on an optical phaenomenon which occurs on viewing a figure of a crystal or geometrical solid, London and Edinburgh Philosophical Magazine and Journal of Science, 1832, 1 (5): 329–337. doi:10.1080/14786443208647909.
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- (en) The Necker Cube avec une applet Java, par S. Flinn, sur le site de l'université de la Colombie-Britannique
- (en) The Boltzmann Machine: Necker Cube Example par David Marshall, université de Cardiff
- (en) Necker Cube: A Visual Illusion sur cut-the-knot
- (en) The bipolarity of figure quality par Lothar Kleine-Horst
Source de la traduction
[modifier | modifier le code]- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Necker Cube » (voir la liste des auteurs).


 French
French Deutsch
Deutsch