French
DeutschDiagramme de bifurcation — Wikipédia
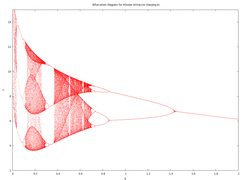
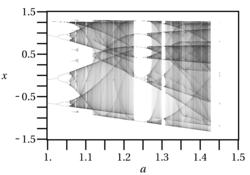
En mathématiques, et en particulier dans l'étude des systèmes dynamiques, un diagramme de bifurcation illustre les valeurs visitées asymptotiquement (points fixes, points périodiques, attracteurs chaotiques) par un système en fonction d'un paramètre[1],[2].
Exemples
[modifier | modifier le code]-
Diagramme de bifurcation pour l'attracteur de Rössler. -
Diagramme de bifurcation pour l'attracteur de Hénon. -
Diagramme de bifurcation de la fonction tente (en). -
Diagramme de bifurcation de la fonction de Gauss itérée (en).
Notes et références
[modifier | modifier le code]- ↑ (en) Tianshou Zhou, « Bifurcation », dans Encyclopedia of Systems Biology, Springer, (ISBN 978-1-4419-9863-7, DOI 10.1007/978-1-4419-9863-7_500, lire en ligne), p. 79–86
- ↑ (en) Christos Volos, Ioannis Kyprianidis, Ioannis Stouboulos et Sundarapandian Vaidyanathan, chap. 7 « Random Bit Generator Based on Non-Autonomous Chaotic Systems », dans Ahmad Taher Azar, Sundarapandian Vaidyanathan, Handbook of Research on Advanced Intelligent Control Engineering and Automation, IGI Global, , 794 p. (ISBN 9781466672482, DOI 10.4018/978-1-4666-7248-2.ch007, lire en ligne), p. 203-229
