Diffusion statique de la lumière — Wikipédia
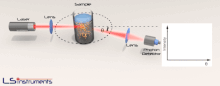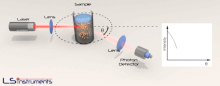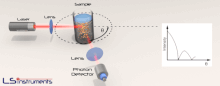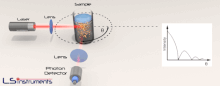
La diffusion statique de la lumière est une technique utilisée en physique et en chimie pour mesurer l'intensité de la lumière dispersée pour obtenir le poids moléculaire moyen Mw d'une macromolécule, comme un polymère ou une protéine en solution.
Explications
[modifier | modifier le code]La mesure de l'intensité de diffusion à de nombreux angles permet le calcul de la racine carrée du rayon moyen, aussi appelé le rayon de giration. En mesurant l'intensité de diffusion pour de nombreux échantillons de diverses concentrations, le second coefficient du viriel A2, peut être calculé[1],[2],[3],[4],[5],[6].
La diffusion statique de la lumière est aussi couramment utilisé pour déterminer la taille des particules en suspensions dans la sub-µm et gammes supra-µm, via, respectivement, la Théorie de Mie et la diffraction de Fraunhofer.
En ce qui concerne les expériences de diffusion de lumière statique, c'est une lumière monochromatique de haute intensité, généralement un laser, qui est envoyée dans une solution contenant des macromolécules. Un ou plusieurs détecteurs sont utilisés pour mesurer l'intensité de diffusion à un ou plusieurs angles. La dépendance angulaire est nécessaire pour obtenir des mesures précises à la fois de masse molaire et de la taille pour toutes les macromolécules de rayon au-dessus de 1 à 2 % de la longueur de l'onde incidente. D'où des mesures simultanées à plusieurs angles par rapport à la direction du rayon incident, connue sous le nom de diffusion de la lumière sous multiples angles (MALS (en)) ou diffusion d'une lumière laser sous multiples angles (MALLS), est généralement considérée comme l'implémentation standard de diffusion de lumière statique.
Pour mesurer la masse moléculaire moyenne directement sans calibration, à partir de l'intensité lumineuse de diffusion, l'intensité du laser, le rendement quantique du détecteur et le volume de la diffusion totale de l'angle solide du détecteur doivent être connus. Comme c'est impossible, tous les instruments commerciaux sont calibrés à l'aide d'un diffuseur comme le toluène.
Théorie
[modifier | modifier le code]Pour un instrument de diffusion de la lumière composée de plusieurs détecteurs placés à des angles différents, les détecteurs doivent réagir de la même manière. Généralement, les détecteurs auront une légère différence d'efficacité quantique, de fait, de légers gains ou pertes seront observables selon la différence de volume de diffusions géométriques. Pour normaliser les détecteurs, une mesure d'un solvant pur est réalisée au préalable. Ensuite, un diffuseur isotrope est ajouté au solvant. De ce fait, les diffuseurs isotropes diffusent la même intensité de lumière à tous les angles, l'efficacité des détecteurs et le gain peuvent donc être normalisées avec cette procédure. Il est convenable de normaliser tous les détecteurs au détecteur d'angle de 90°.
où IR(90) est l'intensité de diffraction mesurée pour la diffusion de Rayleigh par le détecteur d'angle de 90°.
L'équation la plus courante permettant de mesurer la masse moléculaire moyenne en poids, Mw, est l'équation de Zimm :
où
et
avec
et le vecteur de diffusion de la lumière polarisée verticalement est :
avec :
- n0, l'indice de réfraction du solvant ;
- λ, la longueur d'onde de la source lumineuse ;
- NA, le nombre d'Avogadro (6,022×1023 mol−1) ;
- c, la concentration de la solution ;
- dn/dc, la variation de l'indice de réfraction de la solution en fonction de la concentration.
L'intensité de l'analyte (la solution) mesurée à un angle est IA(θ). Dans ces équations, l'indice est noté A pour l'analyte et T est le toluène, avec le quotient de Rayleigh du toluène, RT, étant 1,35×10–5 cm–1 pour un laser hélium-néon. Le rayon de giration Rg et le second coefficient du viriel A2 sont également calculés à partir de cette équation. L'incrément d'indice de réfraction dn/dc caractérise la variation de l'indice de réfraction n à la concentration c, et peut être mesuré à l'aide d'un réfractomètre différentiel.
Une représentation de Zimm est construite à partir d'une double extrapolation à angle zéro et une concentration nulle de plusieurs angles et mesures de concentration. Dans la forme la plus simple, l'équation Zimm est réduite à :
pour les mesures effectuées à faible angle et de dilution infinie puisque P(0) = 1.
Il y a généralement un certain nombre d'études développées pour analyser la diffusion des particules dans une solution pour obtenir les caractéristiques physiques ci-dessus de particules. Une expérience de diffusion de la lumière statique simple, implique l'intensité moyenne de l'échantillon qui est corrigée pour la diffusion du solvant qui donnera le quotient Rayleigh, R, en fonction de l'angle ou le vecteur vague q comme suit :
Analyse de données
[modifier | modifier le code]Représentation de Guinier
[modifier | modifier le code]L'intensité diffusée peut être tracée en fonction de l'angle pour donner des informations sur le rayon de giration (Rg), qui peut simplement être calculé en utilisant l'approximation de Guinier :
où ln(ΔR(θ)) = InP(θ) aussi connu comme le facteur de forme avec q = 4πn0sin(θ/2)/λ. Par conséquent, la détermination du quotient Rayleigh, ΔR(θ) vs sin2(θ/2) ou q2 donnera une pente Rg2/3. Cependant, cette approximation est vraie seulement pour qRg < 1. À noter que pour une représentation de Guinier, la valeur de dn/dc et la concentration n'est pas nécessaire.
Représentation de Kratky
[modifier | modifier le code]La représentation de Kratky est souvent utilisée pour analyser la conformation des protéines, mais elle peut être aussi utilisée pour analyser le modèle de la marche aléatoire de polymères. Une parcelle Kratky peut être faite en représentant sin2(θ/2)ΔR(θ) vs sin(θ/2) ou q2ΔR(θ) vs q.
Représentation de Zimm
[modifier | modifier le code]Pour des polymères qui présentent un caractère mono-dispersé (de dimension équivalente) () déterminé par la diffusion dynamique de la lumière, une courbe de Zimm est un moyen classique d'obtention des paramètres dérivés tels que Rg, la masse moléculaire Mw et le second coefficient du viriel A2.
À noter que si la constante du matériau K définie ci-dessus n'est pas implémentée, la représentation de Zimm ne donnera que Rg. L'implémentation de K donnera l'équation suivante :
Les expériences sont réalisées sous plusieurs angles, qui satisferont la condition qRg < 1, et avec au moins quatre concentrations. L'exécution d'une analyse Zimm sur une seule concentration est connue comme une analyse partielle de Zimm, elle est uniquement valable pour les solutions diluées. La Zimm partielle ne donne cependant pas le second coefficient du viriel, en raison de l'absence de la concentration variable de l'échantillon.
Diffusion de la lumière sous multiples angles
[modifier | modifier le code]La diffusion de lumière statique suppose que chaque photon n'est diffusé qu'une seule fois. Par conséquent, les analyses faites d'après les calculs mentionnés ci-dessus ne seront corrects que si l'échantillon a été dilué suffisamment pour faire en sorte que les photons ne soient pas dispersés plusieurs fois par l'échantillon avant d'être détectés. Les interprétations correctes deviennent extrêmement difficiles à obtenir pour les systèmes avec des contributions non négligeables de la diffusion multiple de la lumière. Dans de nombreux instruments commerciaux où l'analyse du signal de diffusion est automatiquement effectuée, l'erreur ne pourra jamais être remarquée par l'utilisateur. En particulier pour les particules plus grandes et celles ayant un fort contraste d'indice de réfraction, ce qui limite l'application de la dispersion de la lumière statique standard des concentrations très basses de particules. D'autre part, pour les macromolécules solubles qui présentent un contraste relativement faible par rapport à l'indice de réfraction du solvant (y compris la plupart des polymères et des biomolécules dans leurs solvants respectifs), la diffusion multiple est rarement un facteur limitant, même à des concentrations proches de la limite de solubilité.
Cependant, comme le montre Schaetzel[7], il est possible de supprimer la diffusion multiple des expériences de diffusion statique de la lumière par l'intermédiaire d'une approche de corrélation croisée. La méthode consiste à isoler, dans une expérience de diffusion statique de la lumière, la lumière dispersée seule, et de supprimer les contributions indésirables de la diffusion multiple. Différentes implémentations de diffusion de la lumière de corrélation croisée ont été développées et appliquées au cours du temps. En effet, actuellement, le régime le plus largement utilisé est appelé la méthode 3D de diffusion dynamique de la lumière[8],[9]. Cette même méthode peut également être utilisée pour corriger les données de diffusion de la lumière dynamique pour plusieurs essais de diffusions[10].
Notes et références
[modifier | modifier le code]- (de) Albert Einstein, Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes., Allemagne, Annalen der Physik, (DOI 10.1002/andp.19103381612, lire en ligne), tome 338, p. 1275-1298
- ↑ (de) Albert Einstein, Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes, Allemagne, Annalen der Physik, (DOI 10.1002/andp.19103381612, lire en ligne), tome 338, p. 1275-1298
- ↑ (en) C. V. Raman, Indian Journal of Physics. no.12648, Inde, IACS, since 1926 (DOI https://dx.doi.org/10.1063/1.1707436, lire en ligne)
- ↑ (en) P. Debye, Light Scattering in Solutions, New York, AIP, , 338 p. (Bibcode 1944JAP....15..338D, lire en ligne), Page 15
- ↑ (en) Bruno H. Zimm, Molecular Theory of the Scattering of Light in Fluids, New York, AIP, , 141 p. (Bibcode 1945JChPh..13..141Z, lire en ligne), Page 15
- ↑ (en) Bruno H. Zimm, The Scattering of Light and the Radial Distribution Function of High Polymer Solutions, New York, AIP, , 1093 p. (Bibcode 1948JChPh..16.1093Z, lire en ligne), p. 16
- ↑ (en) K Schatzel, Suppression of multiple scattering in photon correlation spectroscopy, Journal of Physics, (DOI https://dx.doi.org/10.1088/0953-8984/2/S/062, lire en ligne)
- ↑ Claus Urban et Peter Schurtenberger, « Characterization of Turbid Colloidal Suspensions Using Light Scattering Techniques Combined with Cross-Correlation Methods », Journal of Colloid and Interface Science, vol. 207, , p. 150–158 (DOI 10.1006/jcis.1998.5769, lire en ligne, consulté le )
- ↑ Ian D. Block et Frank Scheffold, « Modulated 3D cross-correlation light scattering: Improving turbid sample characterization », Review of Scientific Instruments, vol. 81, , p. 123107 (ISSN 0034-6748 et 1089-7623, DOI 10.1063/1.3518961, lire en ligne, consulté le )
- ↑ P. N. Pusey, « Suppression of multiple scattering by photon cross-correlation techniques », Current Opinion in Colloid & Interface Science, vol. 4, , p. 177–185 (DOI 10.1016/S1359-0294(99)00036-9, lire en ligne, consulté le )
Voir aussi
[modifier | modifier le code]Articles connexes
[modifier | modifier le code]Liens externes
[modifier | modifier le code]- Méthodes plus spécifiques, sur malvern.com
- Structure des macromolécules, sur pubs.acs.org


 French
French Deutsch
Deutsch









