Gradient — Wikipédia

Cet article ne cite pas suffisamment ses sources (juillet 2023).

Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ».

En pratique : Quelles sources sont attendues ? Comment ajouter mes sources ?

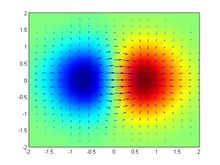
En mathématiques et en physique, le gradient d'une fonction de plusieurs variables est un champ de vecteurs qui combine en chaque point les différentes dérivées partielles et donne ainsi à la fois la direction de la variation la plus forte^[1] localement et l’intensité de cette variation. Pour une fonction représentant l’altitude, il suit les lignes de plus grande pente (dans le sens de la montée), avec une norme égale à cette pente. Lorsque la fonction ne dépend que d’une seule variable réelle, le gradient se confond avec la dérivée usuelle, comme en météorologie où le gradient de température est assimilé au taux de variation de la température selon l'altitude^[2].

Le gradient d’une fonction f est noté grad(f) ou avec l’opérateur nabla ${\displaystyle \nabla f}$, parfois avec des flèches suscrites.

En chaque point où il est défini, le produit scalaire avec le gradient constitue la différentielle de la fonction, c’est-à-dire la partie linéaire de son développement limité à l’ordre 1. Par exemple, pour une fonction de trois variables admettant des dérivées partielles en un point a, pour une petite variation h = (h₁, h₂, h₃), on trouve

${\displaystyle f(a+h)-f(a)\approx \operatorname {d} \!f_{a}(h)=\langle \nabla f_{a},h\rangle ={\frac {\partial f}{\partial x}}(a)\ h_{1}+{\frac {\partial f}{\partial y}}(a)\ h_{2}+{\frac {\partial f}{\partial z}}(a)\ h_{3}.}$

Cette méthode permet d'approcher localement une fonction de plusieurs variables par une forme linéaire.

La notion s’étend aux fonctions réelles définies sur une variété riemannienne.

Le gradient est toujours orthogonal aux lignes de niveau ou aux isosurfaces. Il permet aussi d’exprimer des conditions d’optimisation sous contrainte et intervient dans des méthodes d’analyse numérique pour obtenir des suites minimisantes.

En physique et en analyse vectorielle, le gradient est un vecteur indiquant comment une grandeur physique varie dans l'espace^[a]. Le gradient est d'une importance capitale en physique, qui l'employa avant les autres disciplines. En théorie des variations, il est aussi fondamental dans le domaine de l'optimisation ou de la résolution d'équations aux dérivées partielles.

En sciences de la Terre, le gradient est utilisé pour la variation dans toutes les directions d'un paramètre de la lithosphère, de l'hydrosphère, de l'atmosphère, ou de la biosphère. Cependant, le terme est souvent employé pour la composante dans une seule direction, comme dans le cas de la dérivée verticale d'une grandeur physique, c.-à-d. sa dérivée par rapport à la coordonnée ${\displaystyle z}$ (altitude ou profondeur). Par exemple, le gradient géothermique est la dérivée ${\displaystyle {\tfrac {\partial T}{\partial z}}}$ fois ${\displaystyle {\vec {\mathrm {k} }}}$, où ${\displaystyle T}$ est la température et ${\displaystyle {\vec {\mathrm {k} }}}$ un vecteur unitaire vertical.

Dans un système de coordonnées cartésiennes euclidien, le gradient d'une fonction f différentiable au point ${\displaystyle a=(x_{1},x_{2},\dots ,x_{n})}$ est le vecteur noté ${\displaystyle \nabla f(a)}$ de composantes les ${\displaystyle {\tfrac {\partial f}{\partial x_{i}}}(a)~}$ (où i = 1, 2, ..., n)^[3], c.-à-d. les dérivées partielles de f par rapport aux coordonnées^[4],[5], au point a :

$${\displaystyle \nabla f(a)={\begin{bmatrix}{\frac {\partial f}{\partial x_{1}}}(a)\\\vdots \\{\frac {\partial f}{\partial x_{n}}}(a)\end{bmatrix}}.}$$

Dans un repère orthonormé, si le vecteur gradient n'est pas nul, alors il pointe dans la direction où la fonction croît le plus rapidement, et sa norme est égale au taux de croissance dans cette direction.

Les composantes du gradient de f sont les coefficients des variables dans l'équation réduite de l'espace tangent au point a au graphe de f. Cette propriété lui permet d'être défini indépendamment du choix du système de coordonnées, en tant que champ de vecteurs dont les composantes se transforment lors du passage d'un système de coordonnées à un autre.

La généralisation du gradient aux fonctions différentiables de plusieurs variables et à valeurs vectorielles (et aux applications différentiables entre espaces euclidiens) est la matrice jacobienne. La généralisation aux fonctions entre espaces de Banach est la dérivée de Fréchet.

• La dérivée ou différentielle d'une fonction f en un point a est généralement notée :

f'(a) ou Df(a) ou ${\displaystyle \mathrm {D} f_{a}}$ ou ${\displaystyle \mathrm {D} _{a}f}$ ou ${\displaystyle {\mathcal {D}}_{a}f}$

ou, abusivement puisqu'elle n'est pas infinitésimale :

df(a) ou ${\displaystyle \mathrm {d} f_{a}}$ ou ${\displaystyle \mathrm {d} _{a}f.}$

• Le gradient d'une fonction f en un point a est généralement noté :

${\displaystyle {\overrightarrow {\mathrm {grad} }}\ f(a)}$ ou ${\displaystyle {\overrightarrow {\nabla }}f(a)}$ ou ${\displaystyle {\overrightarrow {\mathrm {grad} }}_{a}f}$ ou ${\displaystyle {\overrightarrow {\nabla }}_{a}f}$.

Le symbole ∇ est appelé nabla. Dans la littérature en anglais, ou parfois en français par commodité typographique, on préfère mettre en gras le symbole du gradient pour signifier son caractère vectoriel :

${\displaystyle \mathbf {grad} \ f}$ ou ∇f.

En notation tensorielle, le vecteur position ${\displaystyle {\vec {x}}}$, contravariant, s'écrit ${\displaystyle x^{n}}$ (indice ${\displaystyle n}$ en position supérieure^[b], ${\displaystyle n}$ variant de 1 au nombre de dimensions de l'espace). Le gradient ${\displaystyle {\vec {g}}}$ d'un champ scalaire ${\displaystyle f({\vec {x}})}$, écrit ${\displaystyle f(x^{n})}$ en notation tensorielle, est covariant et s'écrit donc ${\displaystyle g_{n}}$ (indice ${\displaystyle n}$ en position inférieure). La définition du gradient s'écrit alors^[6] :

${\displaystyle g_{n}={\frac {\partial f}{\partial x^{n}}}}$.

Avec la convention de sommation d'Einstein, la variation infinitésimale de ${\displaystyle f}$ s'écrit :

${\displaystyle \mathrm {d} f=g_{n}\,\mathrm {d} x^{n}}$.

Le gradient de température, ou gradient thermique, est le gradient de la température en tant que fonction scalaire des coordonnées spatiales (lui est une fonction vectorielle de ces coordonnées).

Supposons que l'on place une poutre rectiligne entre deux murs qui n'ont pas la même température, le mur de gauche étant le plus froid. On observe que, sur la poutre, la température varie dans le temps, et dans l'espace : elle augmente de la gauche vers la droite. À ce phénomène thermodynamique, on associe un phénomène de flux de chaleur, lui-même lié à un gradient de température, c.-à-d. à une variation de la température le long de la poutre (cf. Conduction thermique, Loi de Fourier).

À un instant fixé, à chaque point M de la poutre, on attribue une abscisse x ; par exemple, à l'extrémité gauche, l'abscisse x = 0, et à l'extrémité droite, l'abscisse x = L (longueur de la poutre). En chaque point M(x) de la poutre, on considère la température T(x) ; autrement dit, T est fonction de x.

Entre deux points distants d'une très petite longueur δx, on mesure un écart de température δT. Au sens usuel, le gradient (de température) est le rapport entre ces deux grandeurs :

${\displaystyle {\overrightarrow {\operatorname {grad} }}\ T={\frac {\delta T}{\delta x}}\ {\vec {\mathrm {i} }}.}$

Au sens analytique (mathématique), on parle de gradient si ce rapport admet une limite quand δx tend vers 0, limite notée :

${\displaystyle {\overrightarrow {\nabla }}T(x)=T'(x)\ {\vec {\mathrm {i} }}={\frac {\mathrm {d} T}{\mathrm {d} x}}(x)\ {\vec {\mathrm {i} }}.}$

On écrit la variation le long de x comme l'approximation (dite du premier ordre) :

${\displaystyle T(x+\delta x)-T(x)={\frac {\mathrm {d} T}{\mathrm {d} x}}(x)\ \delta x+o(\delta x),}$

où ${\displaystyle o(\delta x)}$ signifie que le terme qui reste est négligeable par rapport à ${\displaystyle \delta x.}$

• Le rapport ${\displaystyle {\tfrac {\delta T}{\delta x}}}$ a un signe, qui correspond à un sens. Dans notre poutre, la température augmente de gauche à droite, donc le gradient est orienté vers la droite ; l'axe des x aussi est orienté de gauche à droite, donc ${\displaystyle {\tfrac {\delta T}{\delta x}}>0.}$
• En dimension 1, les notions de gradient et de dérivée sont équivalentes.
• En physique, la norme de ce gradient est homogène à une température divisée par une distance (mesurée en K·m⁻¹, ou plus usuellement en °C·m⁻¹).

En réalité, la température d'un point de la poutre varie en fonction d'un déplacement dans l'espace. On caractérise un point M de l'espace par ses coordonnées cartésiennes : M(x , y , z). « Comme » précédemment, la température est fonction des coordonnées de M : T(x , y , z).

Pour chacune de ces directions, on peut écrire une variation, dite partielle. Si, tout en étant en 3D, on ne se déplace que selon un axe, par exemple selon les ordonnées y, alors on peut réécrire la même formule que précédemment sur l'accroissement de température. Cependant, pour noter la variation, on passe par l'écriture en dérivée partielle (dite ronde) plutôt que par la dérivée unidimensionnelle (dite droite). On écrit la variation le long de y comme l'approximation (dite du premier ordre) :

${\displaystyle T(x,y+\delta y,z)-T(x,y,z)={\frac {\partial T}{\partial y}}(x,y,z)\ \delta y+o(\delta y),}$

où ${\displaystyle o(\delta y)}$ signifie que le terme qui reste est négligeable par rapport à ${\displaystyle \delta y.}$

Plus généralement, on se déplace dans l'espace d'un point M(x , y , z) à un point M'(x + δx , y + δy , z + δz), et la température passe de T(x , y , z) à T(x + δx , y + δy , z + δz). En première approximation, cette variation est une fonction linéaire de ${\displaystyle {\vec {h}}={\overrightarrow {MM'}}=\delta \ \!{\overrightarrow {\mathrm {O} M}}=(\delta x,\delta y,\delta z)}$, et s'exprime donc comme somme algébrique des variations liées à chacune des composantes de ${\displaystyle {\vec {h}}:}$

${\displaystyle T(x+\delta x,y+\delta y,z+\delta z)-T(x,y,z)={\frac {\partial T}{\partial x}}(x,y,z)\ \delta x+{\frac {\partial T}{\partial y}}(x,y,z)\ \delta y+{\frac {\partial T}{\partial z}}(x,y,z)\ \delta z+o\!\left({\big \|}{\vec {h}}{\big \|}\right),}$

où ${\displaystyle o\!\left({\big \|}{\vec {h}}{\big \|}\right)}$ signifie que le terme qui reste est négligeable par rapport à ${\displaystyle {\big \|}{\vec {h}}{\big \|}.}$

Soit ${\displaystyle {\overrightarrow {\nabla }}T(x,y,z)=\left({\frac {\partial T}{\partial x}}(x,y,z),{\frac {\partial T}{\partial y}}(x,y,z),{\frac {\partial T}{\partial z}}(x,y,z)\right)}$ le vecteur gradient de température. On peut alors réécrire la relation précédente sous la forme :

${\displaystyle T(M+{\vec {h}})-T(M)={\overrightarrow {\nabla }}T(M)\cdot {\vec {h}}+o\!\left({\big \|}{\vec {h}}{\big \|}\right),}$

où ${\displaystyle {\text{«}}\cdot {\text{»}}}$ désigne le produit scalaire usuel sur ${\displaystyle \mathbb {R} ^{3}.}$

• Le gradient est un vecteur de même dimension que l'espace sur lequel porte la température (ici ℝ³), alors que la température est à valeurs scalaires (c.-à-d. que la température en un point est un nombre, pas un vecteur).
• La direction du (vecteur) gradient définit de nouveau la direction du plus froid au plus chaud, mais cette fois en 3D.
• La norme du gradient de température est toujours homogène à K m⁻¹.

Comme pour la différentielle dont il est une variante, le gradient peut être introduit avec le vocabulaire des éléments différentiels. À titre d'exemple, examinons le problème de la variation de l'aire d'un rectangle.

Dans le plan (xOy), considérons un rectangle de côtés x et y. Sa surface S est égale à xy ; elle dépend donc des coordonnées du point M(x,y). En suivant une démarche intuitive, on convient de noter par dx (resp. dy) une variation infinitésimale de la variable x (resp. y). Lorsque le point M fait un déplacement infinitésimal, la surface varie de façon infinitésimale, et on peut écrire que :

${\displaystyle S+\mathrm {d} S=(x+\mathrm {d} x)(y+\mathrm {d} y)=xy+x\ \mathrm {d} y+y\ \mathrm {d} x+\mathrm {d} x\ \mathrm {d} y.}$

On en déduit facilement que :

${\displaystyle \mathrm {d} S=y\ \mathrm {d} x+x\ \mathrm {d} y+\mathrm {d} x\ \mathrm {d} y.}$

Une simple application numérique où x et y seraient des mètres et dx et dy des centimètres illustre que dx dy est négligeable par rapport aux autres grandeurs.

On peut donner un statut mathématique précis aux notations dx et dy (qui sont des formes différentielles), et à la quantité dx dy (qui est alors du second ordre). Le calcul précédent est en fait un calcul de développement limité à l'ordre 1, faisant intervenir les dérivées premières de la fonction xy par rapport à ses deux variables. En négligeant dx dy, on obtient donc :

${\displaystyle \mathrm {d} S\approx y\ \mathrm {d} x+x\ \mathrm {d} y=(y,x)\cdot (\mathrm {d} x,\mathrm {d} y)=\left({\frac {\partial (xy)}{\partial x}},{\frac {\partial (xy)}{\partial y}}\right)\cdot (\mathrm {d} x,\mathrm {d} y)={\overrightarrow {\nabla }}S\cdot \mathrm {d} {\overrightarrow {\mathrm {O} M}},}$

où ${\displaystyle {\overrightarrow {\nabla }}S={\overrightarrow {\mathrm {grad} }}\ S.}$

Bien sûr, on peut utiliser des notations un peu différentes :

${\displaystyle \mathrm {d} S\approx y\ \mathrm {d} x+x\ \mathrm {d} y=(y\ {\vec {\mathrm {i} }}+x\ {\vec {\mathrm {j} }})\cdot (\mathrm {d} x\ {\vec {\mathrm {i} }}+\mathrm {d} y\ {\vec {\mathrm {j} }})=\left({\frac {\partial (xy)}{\partial x}}{\vec {\mathrm {i} }}+{\frac {\partial (xy)}{\partial y}}{\vec {\mathrm {j} }}\right)\cdot (\mathrm {d} x\ {\vec {\mathrm {i} }}+\mathrm {d} y\ {\vec {\mathrm {j} }})={\overrightarrow {\nabla }}(xy)\cdot \mathrm {d} {\overrightarrow {\mathrm {O} M}},}$

où ${\displaystyle {\overrightarrow {\nabla }}(xy)={\overrightarrow {\mathrm {grad} }}\ (xy).}$

L'intérêt d'introduire ces vecteurs pour exprimer la variation d'une fonction de plusieurs variables est de montrer que :

• la fonction varie le plus si le point se déplace dans la direction du vecteur gradient ;
• elle ne varie presque pas s'il se déplace dans toute direction perpendiculaire au gradient.

En effet : ${\displaystyle (y\ {\vec {\mathrm {i} }}+x\ {\vec {\mathrm {j} }})\perp (\mathrm {d} x\ {\vec {\mathrm {i} }}+\mathrm {d} y\ {\vec {\mathrm {j} }})\Longleftrightarrow y\ \mathrm {d} x+x\ \mathrm {d} y=0,}$ « c.-à-d. » ${\displaystyle \ \mathrm {d} S\approx 0.}$

En électrostatique, ceci donne les courbes de même potentiel : les « équipotentielles ».

Soient E un espace vectoriel euclidien, U un ouvert de E, et une fonction ${\displaystyle f:U\to \mathbb {R} }$, différentiable en un point a de U. On note ${\displaystyle \mathrm {D} _{a}f}$ la différentielle en a de f ; c'est une forme linéaire sur E. On note ${\displaystyle \mathrm {D} _{a}f\left(h\right)}$ l'image par cette différentielle d'un vecteur h de E.

Il existe un unique vecteur A tel que pour tout vecteur h de E, ${\displaystyle \ \mathrm {D} _{a}f\left(h\right)=\langle A\mid h\rangle }$, où ${\displaystyle \langle \cdot \mid \cdot \rangle }$ désigne le produit scalaire sur E.

Le vecteur A est appelé le gradient de f en a, et il est noté ${\displaystyle \nabla _{a}f}$. Il vérifie donc :

${\displaystyle \forall \ h\in E,\quad \langle \nabla _{a}f\mid h\rangle =\mathrm {D} _{a}f\left(h\right).}$

Si une application ${\displaystyle f:U\to \mathbb {R} }$ est différentiable en un point a, alors on peut écrire le développement limité de f du premier ordre au voisinage de a (avec la notation de Landau)^[7]:

${\displaystyle \forall \ h\in E,\quad f(a+h)=f(a)+\langle \nabla f(a)\mid h\rangle +o{\big (}\|h\|{\big )}.}$

Puisque le gradient est lui-même un vecteur de E, il est naturel qu'on cherche à l'exprimer dans une base orthonormée ${\displaystyle (\mathbf {e} _{1},\dots ,\mathbf {e} _{n})}$ de cet espace vectoriel. On démontre qu'il s'exprime à l'aide des dérivées partielles sous la forme :

${\displaystyle \nabla f(a)=\sum _{i=1}^{n}\left[{\frac {\partial f}{\partial x_{i}}}(a)\ \mathbf {e} _{i}\right].}$

Par exemple, en dimension 3, on obtient :

${\displaystyle \nabla f(a)={\frac {\partial f}{\partial x_{1}}}(a)\ \mathbf {e} _{1}+{\frac {\partial f}{\partial x_{2}}}(a)\ \mathbf {e} _{2}+{\frac {\partial f}{\partial x_{3}}}(a)\ \mathbf {e} _{3}.}$

Le gradient de f désigne la direction où la pente de f est la plus grande. Précisément^[4] :

Soit un point ${\displaystyle a\in U}$ tel que f est différentiable en a et que ${\displaystyle \nabla f(a)\neq 0\ ;}$ pour tout vecteur ${\displaystyle v\in \mathbb {R} ^{n}}$ tel que ${\displaystyle \|v\|=\|\nabla f(a)\|,}$ il existe ${\displaystyle \delta >0}$ tel que :

${\displaystyle \forall \ t\in \ \!]0,\delta [,\quad f(a+t\ \!v)\leq f{\big (}a+t\ \nabla f(a){\big )}.}$

Soit ${\displaystyle f:x\in E\mapsto f(x)\in \mathbb {R} }$ une fonction de classe C¹. Un changement de paramètres consiste à introduire un difféomorphisme ${\displaystyle \Phi :a\in \mathbb {R} ^{n}\mapsto x=\Phi (a)\in E}$, où n est la dimension de E. On exprime alors le gradient de f dans une base de E, dite locale, formée des vecteurs ${\displaystyle {\frac {\partial \Phi }{\partial a_{i}}}}$, les dérivées partielles étant celle de la fonction composée ${\displaystyle f\circ \Phi }$ par rapport aux ${\displaystyle a_{i}}$. Si la base locale est orthogonale, on préfère généralement utiliser la base orthonormée associée, obtenue en divisant chaque vecteur de la base locale par sa norme euclidienne.

C'est ainsi que le passage dans le plan en coordonnées polaires permet d'exprimer le gradient en fonction des dérivées partielles de la fonction composée f(r,θ) par rapport à l'abscisse polaire (r) et à l'argument (θ), la base utilisée étant constituée du vecteur radial unitaire et de son orthogonal.

En dimension 3, on obtient ainsi les formules suivantes :

• En coordonnées cylindriques (pour les coordonnées polaires, ne pas considérer la composante en z) :

${\displaystyle \nabla f={\frac {\partial f}{\partial \rho }}\mathbf {e} _{\rho }+{\frac {1}{\rho }}{\frac {\partial f}{\partial \theta }}\mathbf {e} _{\theta }+{\frac {\partial f}{\partial z}}\mathbf {e} _{z},}$

qu'on peut aussi noter :

${\displaystyle \nabla f={\frac {\partial f}{\partial \rho }}\mathbf {e} _{\rho }+{\frac {1}{\rho }}{\frac {\partial f}{\partial \phi }}\mathbf {e} _{\phi }+{\frac {\partial f}{\partial z}}\mathbf {e} _{z},}$

tout dépend des notations utilisées. Voir :

• En coordonnées sphériques :

${\displaystyle \nabla f={\frac {\partial f}{\partial r}}\mathbf {e} _{r}+{\frac {1}{r}}{\frac {\partial f}{\partial \theta }}\mathbf {e} _{\theta }+{\frac {1}{r\sin \theta }}{\frac {\partial f}{\partial \phi }}\mathbf {e} _{\phi };}$

les vecteurs de type ${\displaystyle \mathbf {e} _{r}}$ sont utilisés en coordonnées polaires.

Soient ${\displaystyle {\big (}H,\langle \cdot \mid \cdot \rangle {\big )}}$ un espace de Hilbert (de dimension finie ou non), U un ouvert de H, et une application ${\displaystyle f:U\to \mathbb {R} }$, différentiable en un point a de U. La différentielle Df(a) étant, par définition, une forme linéaire continue sur H, il résulte du théorème de représentation de Riesz qu'il existe un unique vecteur, noté ${\displaystyle \nabla f(a)}$, de H tel que :

${\displaystyle \forall \ h\in H,\quad \mathrm {D} f(a)\left(h\right)=\langle \nabla f(a)\mid h\rangle .}$

Le vecteur ${\displaystyle \nabla f(a)}$ est appelé le gradient de f en a.

On montre que si ${\displaystyle \nabla f(a)\neq 0}$, alors f croît strictement dans la direction de ${\displaystyle \nabla f(a)}$ en passant par a, c.-à-d. :

Il existe ${\displaystyle \alpha >0}$ tel que pour tous s et t de ${\displaystyle ]-\alpha ,\alpha [,}$

${\displaystyle s<t\Longrightarrow f{\big (}a+s\ \nabla f(a){\big )}<f{\big (}a+t\ \nabla f(a){\big )}.}$

On peut encore étendre cette définition à une fonction définie et différentiable sur une variété riemannienne (M,g). Le gradient de f en a est alors un vecteur tangent à la variété en a, défini par :

${\displaystyle \forall \ h\in \mathrm {T} _{a}M,\quad \mathrm {D} f(a)\left(h\right)=g{\big (}\nabla f(a)\mid h{\big )}.}$

Enfin, si f est un champ scalaire indépendant du système de coordonnées, c'est un tenseur d'ordre 0, et sa dérivée partielle est égale à sa dérivée covariante :

${\displaystyle (\nabla f)_{i}=\partial _{i}f=f_{,i}=f_{;i}\ .}$

En coordonnées contravariantes, on calcule le champ de vecteurs appelé gradient de f :

${\displaystyle (\nabla f)^{i}=g^{ij}~f_{;j}\ .}$

Cette formule permet, une fois établi le tenseur métrique, de calculer facilement le gradient dans tout système de coordonnées.

Classiquement, le gradient permet de définir la « normale aux courbes de niveau », ce qui se traduit en 2D et en 3D par des propriétés géométriques intéressantes. La propriété de tangence étant liée à la convexité/concavité, il est aussi intéressant de voir le lien qui existe entre gradient et convexité, toujours en 2D ou 3D.

Soient une application ${\displaystyle f:\mathbb {R} ^{2}\to \mathbb {R} }$ continûment différentiable, et une courbe définie par l'équation f(u) = k, où k est une constante. En un point v donné de cette courbe, si le gradient existe et s'il n'est pas nul, alors il donne la direction de la normale en v à la courbe ; la droite tangente en v à la courbe est alors orthogonale au gradient.

Application au traitement d'image

Soient une application ${\displaystyle f:\mathbb {R} ^{3}\to \mathbb {R} }$ continûment différentiable, et une surface définie par l'équation f(u) = k, où k est une constante. En un point v donné de cette surface, si le gradient existe et s'il n'est pas nul, alors il donne la direction de la normale en v à la surface ; le plan tangent en v à la surface est alors orthogonal au gradient.

Soient ${\displaystyle n\in \mathbb {N} ^{*}}$ (par exemple, n = 2 ou n = 3), et une application ${\displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$ continûment différentiable. Si l'application ${\displaystyle \mathbf {\nabla } f:\mathbb {R} ^{n}\to \mathbb {R} ^{n}}$ est monotone (resp. strictement monotone), alors f est convexe (resp. strictement convexe), c.-à-d., en utilisant la caractérisation par les cordes :

${\displaystyle \forall (u,v)\in \left(\mathbb {R} ^{3}\right)^{2},\mathbf {\nabla } _{u}f\cdot \mathbf {\nabla } _{v}f\geq 0\Rightarrow \forall (u,v,\lambda )\in \mathbb {R} ^{3}\times \mathbb {R} ^{3}\times [0,1],f{\big (}\lambda u+(1-\lambda )v{\big )}\leq \lambda f(u)+(1-\lambda )f(v).}$

Cette propriété est intéressante parce qu'elle reste valable même si f n'est pas deux fois différentiable.

Si f est deux fois différentiable, le hessien est positif si et seulement si le gradient est monotone.

La monotonie telle que définie ci-dessus permet de définir une fonction dérivée croissante ou décroissante au sens usuel. Dans le premier cas, on parle de fonction convexe ; dans le second, de fonction concave.

Si la fonction est deux fois dérivable, la croissance de la dérivée (donc du gradient) est assurée par la positivité de la dérivée seconde (équivalent du hessien).

Cette section ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires indépendantes du sujet.
Pour l'améliorer, ajoutez-en, ou placez des modèles {{Source secondaire souhaitée}} ou {{Source secondaire nécessaire}} sur les passages mal sourcés. (avril 2023)

En analyse vectorielle, le gradient peut être combiné à d'autres opérateurs : divergence (div), rotationnel (rot), laplacien (Δ). Soit f une fonction décrivant un champ scalaire, que l'on suppose de classe C² par rapport à chaque paramètre ; alors :

${\displaystyle {\frac {\partial }{\partial t}}\left({\overrightarrow {\mathrm {grad} }}f\right)={\overrightarrow {\mathrm {grad} }}{\frac {\partial f}{\partial t}}\ ;}$

${\displaystyle \mathrm {div} \left({\overrightarrow {\mathrm {grad} }}f\right)=\Delta f\ ;}$

${\displaystyle {\overrightarrow {\mathrm {rot} }}\left({\overrightarrow {\mathrm {grad} }}f\right)={\overrightarrow {0}}.}$

• (en) Serge Lang, Fundamentals of Differential Geometry, Springer
• (en) Barrett O'Neill, Elementary Differential Geometry, 2^e éd. révisée (ISBN 9780120887354)

• Nabla
• Algorithme du gradient
• Analyse vectorielle
• Dérivée directionnelle
• Gradient projeté
• Opérateur laplacien
• Théorème du gradient

v · m Analyse vectorielle
Objets d'étude	Champ de vecteurs Champ scalaire Équation aux dérivées partielles Équation de Laplace Équation de Poisson
Opérateurs	Nabla Gradient Rotationnel Rotationnel du rotationnel Divergence Laplacien scalaire Bilaplacien Laplacien vectoriel D'alembertien Advection
Théorèmes	Théorème de Green Théorème de Stokes Théorème de Helmholtz-Hodge Théorème de la divergence Théorème du gradient Théorème du rotationnel

• Portail de l'analyse