French
DeutschPavage carré — Wikipédia
Pour les articles homonymes, voir Pavage (homonymie).
Cet article est une ébauche concernant la géométrie.
Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants.
| Pavage carré | |
 | |
| Type | Pavage régulier du plan euclidien |
|---|---|
| Configuration de sommet | 4.4.4.4 (ou 44) |
| Symbole de Schläfli | {4,4} |
| Symbole de Wythoff | 4 | 2 4 |
| Diagramme de Coxeter-Dynkin |      |
| Dual | Auto-dual |
| Groupe de symétrie | p4m |
| Propriétés | Sommet-transitif Arête-transitif Face-transitif |
modifier  | |
Le pavage carré est, en géométrie, un pavage du plan euclidien constitué de carrés.
C'est l'un des trois pavages réguliers du plan euclidien, avec le pavage triangulaire et le pavage hexagonal.
Propriétés
[modifier | modifier le code]Le pavage carré possède un symbole de Schläfli de {4,4}, signifiant que chaque sommet est entouré par 4 carrés.
Symétries
[modifier | modifier le code]Les symétries du pavage carré sont les symétries du carré, les translations, et leurs combinaisons. Elles forment un groupe de symétrie dénommé p4m.
Les symétries du carré forment un sous-groupe, dénommé Groupe diédral d'ordre 8. Ce groupe possède 8 éléments, dont deux éléments générateurs sont, par exemple :
- R, rotation de quart de tour vers la droite
- S, symétrie axiale, d'axe horizontal.
Les 8 symétries du carré sont alors : I (Identité), R, R² (Symétrie centrale), R³ (Rotation inverse), S, RS (Symétrie suivant la première diagonale), R²S (Symétrie d'axe vertical), R³S (Symétrie suivant la deuxième diagonale).
Les translations sont en nombre infini. Elles sont engendrées par la translation unitaire horizontale et la translation unitaire verticale.
Coloration uniforme
[modifier | modifier le code]Il y a 9 colorations uniformes distinctes.
| 9 colorations uniformes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1111 | 1212 | 1213 | 1112i | 1122 | |||||||
 |  |  |  |  | |||||||
| p4m (*442) | p4m (*442) | pmm (*2222) | |||||||||
| 1234 | 1123i | 1123ii | 1112ii | ||||||||
 |  |  |  | ||||||||
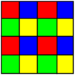| pmm (*2222) | cmm (2*22) | ||||||||||
