Pouvoir de résolution — Wikipédia

Pour les articles homonymes, voir Pouvoir et Résolution.

Le pouvoir de résolution, ou pouvoir de séparation, pouvoir séparateur, résolution spatiale, résolution angulaire, exprime la capacité d'un système optique de mesure ou d'observation – les microscopes, les télescopes ou l'œil, mais aussi certains détecteurs, particulièrement ceux utilisés en imagerie – à distinguer les détails. Il peut être caractérisé par l'angle ou la distance minimal(e) qui doit séparer deux points contigus pour qu'ils soient correctement discernés^[1]. Il peut, de façon équivalente, être caractérisé par la fréquence spatiale maximale que le système permet de mesurer ou restituer : il est alors exprimé en cycles par millimètre (cy/mm) ou en paires de lignes par millimètre (pl/mm)^[2].

La définition du pouvoir de résolution peut tout aussi bien s'appliquer à une capacité de résolution spatiale, spectrale^[3] que temporelle^[4].

Les instruments optiques contiennent le plus souvent une chambre noire, la lumière passant par l'ouverture de la chambre noire subit une diffraction. Même si le système optique est considéré parfait dans les sens où il est dénué de toute aberration, la diffraction limite son pouvoir de résolution : un objet ponctuel donne une image « floue », appelée tache d'Airy. Si deux détails d'un objet sont trop proches, les taches de diffraction se chevauchent et il devient impossible d'obtenir des images séparées de ces détails.

Pour un instrument optique d'ouverture circulaire de diamètre ${\displaystyle D}$ (en mètre) traversé par une onde monochromatique de longueur d'onde ${\displaystyle \lambda }$ (en mètre), la figure de diffraction obtenue, nommée tache d'Airy, présente un premier cercle noir pour un angle par rapport à l'axe de révolution (en radian) de^[5] :

${\displaystyle \theta \simeq 1,22\lambda /D}$.

Plusieurs critères différents peuvent être utilisés selon les domaines d'application. Ils donnent une condition sur la distance entre deux taches d'Airy permettant la séparation entre les points^[6] ; ils sont valables pour des systèmes optiques à symétrie de révolution^[7].

• Le critère de Schuster stipule que deux pics sont séparables pour une configuration où leurs lobes centraux ne se recouvrent pas^[8]. Le critère de Shuster est plus contraignant que celui de Rayleigh et deux points doivent donc être espacés d'un angle supérieur à ${\displaystyle \Delta \theta \simeq 2{,}44\,\lambda /D}$.
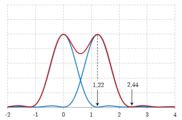
• Le critère de Rayleigh stipule que deux pics sont séparables pour une configuration où la première annulation du disque correspond au maximum du second^[9]. Deux points doivent donc être espacés d'un angle supérieur à ${\displaystyle \Delta \theta \simeq 1{,}22\,\lambda /D}$.

• Le critère de Sparrow stipule que deux pics sont séparables si la dérivée seconde de l'éclairement s'annule^[10] (point d'inflexion), autrement dit si la forme de la somme des deux pics ressemble encore à une selle de cheval. Ce critère, utilisé en astronomie, pondère par 0,84 le résultat obtenu avec le critère de Rayleigh^[11] : ${\displaystyle \Delta \theta \simeq 1{,}02\,\lambda /D}$.

• 
  a. Critère de Schuster.
• 
  b. Critère de Rayleigh.
• 
  c. Critère de Sparrow.
• 
  d. Les deux taches ne sont pas discernables.

Seul le critère de Rayleigh sera retenu dans le reste de l'article.

Dès lors que l'on s'intéresse à une image formée sur un écran ou une surface photosensible, on préfère donner la résolution comme la distance ${\displaystyle \Delta r}$ entre deux points qui pourront être discernés :

${\displaystyle \Delta r=L\,\tan(\Delta \theta )\simeq 1{,}22{\frac {\lambda }{D}}L}$, où ${\displaystyle L}$ est la distance qui sépare la pupille circulaire et la surface cible.

En ce qui concerne les objectifs photographiques, si la surface photosensible se situe dans le plan focal (mise au point à l'infini) à une distance ${\displaystyle f}$ du diaphragme, la résolution d'un objectif parfait seulement limité par la diffraction ne dépend que du nombre d'ouverture ${\displaystyle N}$. La distance minimale qui doit séparer deux points est donnée par :

${\displaystyle \Delta r\simeq 1{,}22{\frac {\lambda }{D}}f\simeq 1{,}22\,\lambda \,N}$.

Enfin, si on parle plutôt d'alternance de lignes successives noires et blanches, la distance ${\displaystyle \Delta r}$ est la distance entre deux lignes noires, soit une paire de lignes. Le pouvoir de résolution du fait de la diffraction s'exprime en termes de fréquence spatiale maximale (généralement exprimée en cycles par millimètre ou paires de lignes par millimètre) :

${\displaystyle f_{S}={\frac {1}{\Delta r}}={\frac {1}{1{,}22\,\lambda \,N}}}$.

Cette limite, fixée par le critère de Rayleigh, apparaît sur les courbes de fonctions de transfert de modulation (FTM) pour un contraste à environ 9 %.

Le pouvoir de résolution de l'œil est d'environ une minute d'arc (1' = 1°/60 = 0,017°) pour une acuité visuelle considérée comme normale à 10/10, soit environ 100 km sur la surface de la Lune vue de la Terre, ou plus proche de nous, un détail d'environ 1 mm pour un objet ou une image situé à 3 m de distance, ou 30 cycles noir/blanc par degré. En pratique, certaines personnes peuvent atteindre 0,5 minute d'arc, ce qui correspond à une vision à une acuité visuelle de 20/10^[12]. Le pouvoir séparateur est limité par la densité de cônes au niveau de la partie la plus sensible de la rétine. Il est intéressant de constater que cette densité est naturellement optimisée pour correspondre à la limite de diffraction.

L'image ci-dessous fait apparaître un même sujet avec trois résolutions différentes. À partir d'une certaine distance, l'œil ne fait plus la différence. Il est alors possible de déterminer la résolution d'un ou des deux yeux : il s'agit du rapport entre la taille des gros pixels (image de droite) et la distance à partir de laquelle on ne perçoit plus de différence entre les images.

Il n'existe pas de norme d'écrans certifiant une résolution dépassant le pouvoir de résolution de la vision humaine.

Pour un télescope de 10 m de diamètre, et pour une longueur d'onde de 550 nm au milieu du domaine visible, le pouvoir de résolution théorique est d'environ 0,014 seconde d'arc^[a] (3,8 × 10^-6 degré), mais il ne peut être atteint sans l'usage d'optique adaptative en raison de la turbulence atmosphérique qui « floute » les images. Pour obtenir une meilleure résolution, on peut utiliser une optique de plus grand diamètre : c'est ce qui justifie la course aux grands télescopes. Une variante est d'utiliser l'interférométrie entre des télescopes distants.

Outil	Diamètre (m)	${\displaystyle \Delta \theta }$ (rad)	${\displaystyle \Delta \theta }$ (")	Détails sur la Lune	Détails à 200 km
Œil	0,0025	2,7 × 10-4	55	103 km	53 m
	0,010	6,7 × 10-5	13	25 km	13 m
Jumelles	0,050	1,3 × 10-5	2,8	5 km	2,7 m
	0,10	6,7 × 10-6	1,4	2,6 km	1,3 m
Télescope 150 mm	0,15	4,5 × 10-6	0,92	1,7 km	89 cm
	0,20	3,4 × 10-6	0,69	1,3 km	67 cm
Télescope 1 m	1,0	6,7 × 10-7	0,14	260 m	13 cm
Hubble	2,4	2,8 × 10-7	0,058	110 m	55 mm
James-Webb	6,5	1,0 × 10-7	0,021	39 m	20 mm
VLT	8,0	8,4 × 10-8	0,017	32 m	16 mm
Télescopes du Keck	10	6,7 × 10-8	0,014	25 m	13 mm
E-ELT (2025)	40	1,7 × 10-8	0,0035	6 m	3,3 mm
Les calculs ci-dessus sont effectués, comme précédemment, avec le critère de Rayleigh et pour une longueur d'onde de 550 nm.

Pour un microscope optique de 1 cm de diamètre, le pouvoir de résolution théorique est d'environ 14 secondes d'arc^[b] (3,8 × 10^-3 degré). Pour un échantillon situé à 1 cm, ce microscope permettrait de distinguer deux points situés à 0,67 μm^[b]. Afin d'obtenir une meilleure résolution l'observation peut être effectuée à des longueurs d'onde plus petites grâce aux ultraviolets en microscopie optique. La microscopie électronique exploite aussi ce phénomène en utilisant des électrons de très faible longueur d'onde.

Les fabricants d'objectifs^[13], de négatifs^[14] ou de capteurs fournissent des courbes de fonction de transfert de modulation (FTM), qui constituent une autre façon de présenter la capacité d'un système à restituer les détails. La résolution est fournie sous forme d'une fréquence spatiale en cycles par millimètre^[13],[14] ou en nombre de lignes par hauteur d'image^[15]. Cependant, il est possible d'évaluer le pouvoir de résolution pour les surfaces photosensibles ou pour les objectifs selon les critères précédemment cités. La résolution d'un appareil de prise de vue est le résultat de la combinaisons des effets de l'objectif et de la surface photosensible.

Le pouvoir de résolution d'un négatif photographique est limité par la finesse des grains de l'émulsion : il est de l'ordre de 50 à 100 paires de lignes par millimètre^[16],[14].

Pour un capteur photographique, la résolution est limitée par la définition du capteur. Selon le théorème d'échantillonnage de Nyquist-Shannon, pour un capteur 24 × 36 mm de 3 840 × 5 760 pixels^[17], la résolution est de 80 pl/mm ; il faudrait pondérer cette valeur à la baisse par un facteur de Kell (en) prenant en compte l'ouverture des pixels (le fait qu'ils ne soient pas ponctuels). De plus, les capteurs sont souvent précédés d'un filtre passe bas (filtre antialiasing ou anticrénelage) qui permet la formation d'une image légèrement floue afin d'éviter le moiré mais qui diminue la résolution. Cependant, bien souvent, l'objectif est le facteur limitant.

Dans le cas des petites ouvertures, le pouvoir de résolution est limité par le phénomène de la diffraction comme présenté au paragraphe précédent. Les résultats des calculs rassemblés dans le tableau ci-dessous sont indépendants du format utilisé : il en découle le fait que les petits capteurs sont plus affectés que les gros par la diffraction. La tache d'Airy est bien plus grosse qu'un pixel pour les petits capteurs dès les ouvertures moyennes.

Nombre d'ouverture	f /2,8	f /4	f /5,6	f /8	f /11	f /16	f /22
Diamètre de la tache d'Airy (μm)	3,8	5,4	7,6	11	15	21	30
Distance minimale entre deux points (μm) ${\displaystyle \Delta r}$	1,9	2,7	3,8	5,4	7,6	11	15
Fréquence spatiale (pl/mm) ${\displaystyle f_{S}}$	530	370	260	190	130	93	66
Les calculs ci-dessus sont effectués, comme précédemment, avec le critère de Rayleigh et pour une longueur d'onde de 550 nm.

Pour les grandes ouvertures, la diffraction devient négligeable : l'image est principalement perturbée par les diverses aberrations. Les objectifs présentent généralement un pouvoir de résolution optimum pour les ouvertures moyennes.

• Diffraction
• Tache d'Airy
• Instrument d'optique
• Étoile double utilisée pour évaluer le pouvoir de séparation d'un télescope

• Portail de la physique
• Portail de l’astronomie
• Portail de l’optique