Problème des distances distinctes d'Erdős — Wikipédia

En géométrie discrète, le problème des distances distinctes d'Erdős concerne le nombre de distances distinctes possibles entre n points distincts du plan euclidien, nombre au sujet duquel plusieurs conjectures ont été posées par Paul Erdős, en 1946^[1], et en 1996^[2]. Elles concernent en particulier le minimum ${\displaystyle f(n)}$ du nombre de distances distinctes^[3]. Erdős et Guy ont aussi étudié les sous-ensembles de ${\displaystyle \mathbb {Z} ^{2}}$ présentant inversement le maximum de distances possibles^[4],[5].

Dans son article de 1946, Erdős démontre l'encadrement ${\displaystyle {\sqrt {n-3/4}}-1/2\leqslant f(n)\leqslant cn/{\sqrt {\ln n}}}$ pour une certaine constante ${\displaystyle c}$^[1]. Le minorant est calculé par un raisonnement élémentaire^[6], et le majorant est donné par l'utilisation d'une grille rectangulaire de dimensions ${\displaystyle {\sqrt {n}}\times {\sqrt {n}}}$ (car il y a ${\displaystyle O(n/{\sqrt {\ln n}})}$ nombres inférieurs à ${\displaystyle n}$ qui sont somme de deux carrés, voir constante de Landau-Ramanujan). Erdős a conjecturé que le majorant est une estimation assez précise de ${\displaystyle f(n)}$, c'est-à-dire que ${\displaystyle f(n)=\Omega (n/{\sqrt {\ln n}})}$ (voir notation de Landau).

En 2010, Larry Guth et Nets Hawk Katz annoncent avoir une solution^[7],[8] ; elle est publiée en 2015 par les Annals of Mathematics^[9], mais démontre seulement la minoration f(n) = Ω(n/ln n).

La minoration f(n) = Ω(n^1/2) donné par Paul Erdős en 1946 a été successivement amélioré :

• f(n) = Ω(n^2/3) (Leo Moser, 1952),
• f(n) = Ω(n^5/7) (Fan Chung, 1984)^[10],
• f(n) = Ω(n^4/5/ln n) (Fan Chung, Endre Szemerédi, W. T. Trotter, 1992),
• f(n) = Ω(n^4/5) (László Székely, 1993),
• f(n) = Ω(n^6/7) (József Solymosi, C. D. Tóth, 2001),
• f(n) = Ω(n^{(4e/(5e − 1)) − e}) (Gábor Tardos, 2003),

  

• f(n) = Ω(n^{((48 − 14e)/(55 − 16e)) − e}) (Nets Katz, Gábor Tardos, 2004),
• f(n) = Ω(n/ln n) (Guth et Katz 2015)

Dans son article de 1946, Erdős conjecture que si les ${\displaystyle n}$ points forment un polygone convexe alors le nombre minimal de distances distinctes est ${\displaystyle \geqslant \left\lfloor {\frac {n}{2}}\right\rfloor }$ avec égalité lorsqu'ils forment un polygone régulier^[1].

Les valeurs de ${\displaystyle f(n)}$ sont connues jusqu'à ${\displaystyle n=13}$ ( suite A186704 de l'OEIS) :

${\displaystyle n}$	2	3	4	5	6	7	8	9	10	11	12	13
${\displaystyle f(n)}$	1	1	2	2	3	3	4	4	5	5	5	6

Jusqu'à ${\displaystyle n=11}$, ${\displaystyle f(n)=\left\lfloor {\frac {n}{2}}\right\rfloor }$ (le minimum est atteint entre autres par le n-gone régulier) ; pour ${\displaystyle n=9}$, Erdős a trouvé trois autres configurations que l'ennéagone^[2],[11].

Pour ${\displaystyle n=12}$, le dodécagone régulier n'est plus minimal ; ${\displaystyle f(12)=5}$ est atteint par une configuration utilisant des nœuds du réseau hexagonal^[2],[11].

Erdős définit ${\displaystyle g(k)}$ comme le nombre maximal de points du plan définissant ${\displaystyle k}$ distances distinctes ; ${\displaystyle g}$ est en quelque sorte la réciproque de ${\displaystyle f}$ :

- ${\displaystyle f(g(k))\leqslant k}$, et ${\displaystyle f(g(k))=k}$ si ${\displaystyle g(k-1)<g(k)}$^[2],

- ${\displaystyle g(f(n))\geqslant n}$, et ${\displaystyle g(f(n))=n}$ si ${\displaystyle f(n+1)>f(n)}$.

Les valeurs de ${\displaystyle g(k)}$ sont connues jusqu'à ${\displaystyle k=6}$ (suite A131628 de l'OEIS) :

${\displaystyle k}$	1	2	3	4	5	6
${\displaystyle g(k)}$	3	5	7	9	12	13

Erdős conjecture que pour ${\displaystyle k\geqslant 7}$ il existe des ensembles de nœuds du réseau hexagonal de taille ${\displaystyle g(k)}$^[2].

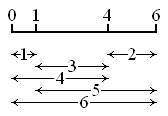
Un exemple d'ensemble de ${\displaystyle n}$ points du plan présentant les ${\displaystyle n(n-1)/2}$ distances possibles entre eux est formé des points de coordonnées ${\displaystyle (2^{k},0),k=0,\dots ,n-1}$ ; il s'agit d'un cas particulier de règle de Golomb, ensemble de ${\displaystyle n}$ points de ${\displaystyle \mathbb {Z} }$ présentant les ${\displaystyle n(n-1)/2}$ distances possibles. Il existe des règles de Golomb plus courtes que celle des puissances de 2 ; par exemple ${\displaystyle \{1,2,5,7\}}$ est plus courte que ${\displaystyle \{1,2,4,8\}}$. La liste des longueurs des règles de Golomb les plus courtes est donnée par la suite A003022 de l'OEIS :

${\displaystyle n}$	2	3	4	5	6	7	8	9	10
${\displaystyle a(n)}$	1	3	6	11	17	25	34	44	55

Passant en dimension 2, Erdős et Guy ont posé en 1970 le problème d'évaluer les dimensions du plus petit carré de ${\displaystyle \mathbb {Z} ^{2}}$ contenant ${\displaystyle n}$ points présentant les ${\displaystyle n(n-1)/2}$ distances possibles^[4],[12].

La liste du nombre de points ${\displaystyle b(n)}$ sur le côté d'un tel carré est donnée par la suite A193838 de l'OEIS :

${\displaystyle n}$	2	3	4	5	6	7	8	9	10	11	12	13	14
${\displaystyle b(n)}$	2	3	4	5	6	7	9	10	11	13	15	16	18

Un dénombrement élémentaire montre que ${\displaystyle n(n-1)/2\leqslant b(n)(b(n)+1)/2-1}$, donc que ${\displaystyle b(n)\geqslant n}$^[4],[12].

• Conjecture de Falconer (en)
• Graphe distance-unité

• Portail de la géométrie