Signal (théorie des systèmes) — Wikipédia

Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (octobre 2014).

Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires.

L'article doit être débarrassé d'une partie de son jargon (octobre 2014).

Sa qualité peut être largement améliorée en utilisant un vocabulaire plus directement compréhensible. Discutez des points à améliorer en page de discussion.

En théorie des systèmes et de l'information, un signal est une quantité mesurable porteuse d’information. On peut classer les signaux par leur usage, le type de message qu'ils portent ou le moyen de transmission. Nous sommes tous les jours exposés à des signaux prenant des formes diverses tels que les signaux textuels, audios, visuels et audiovisuels. L'information contenue dans un signal peut être récupérée à partir de capteurs sous une forme brute, souvent difficile à exploiter. C'est pourquoi il est courant de traiter cette information de telle sorte à y extraire ce qui est utile (par exemple, débruiter une photo). Il existe concrètement de nombreux traitements que l'on peut faire sur un signal tels que l'analyse, le filtrage, le codage, le stockage, etc.^[1]

Un signal peut être représenté de façon mathématique par une fonction réelle ou complexe. Dans ce cadre, un signal est caractérisé par sa nature discrète (signal discret) ou continue (signal analogique), déterministe ou aléatoire, et l'information qu'il porte.

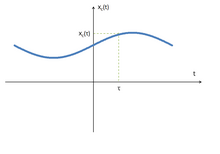
• Un signal est qualifié d' « analogique » : ${\displaystyle x(t)}$ : ${\displaystyle t}$ appartient à ${\displaystyle X\subseteq \mathbb {R} }$.

lorsqu’il ne dépend que d’une variable indépendante, qui peut prendre un continuum de valeurs et qui est ordonnée, c’est-à-dire qu’on lui associe une notion de passé et de futur.

Par exemple, le courant ${\displaystyle i(t)}$ dans un circuit électrique est un signal analogique au même titre que le cours d'une monnaie.

• Un signal est qualifié de « discret ou échantillonné » : ${\displaystyle x[k]}$ : ${\displaystyle k}$ appartient à  ${\displaystyle X\subseteq \mathbb {Z} }$.

lorsqu'il ne peut prendre seulement un ensemble de valeurs discrètes.

Par exemple, un mot est un signal discret car chaque lettre qui le compose doit appartenir à un alphabet de taille finie. De la même façon, une image peut être considérée comme un signal discret car un pixel ne peut prendre qu'un nombre fini de valeurs^[2].

Remarque : Une grande majorité des signaux d’origine physique sont analogiques. Lorsque l'on veut traiter ou stocker ces signaux sur des supports numériques, nous devons les échantillonner, c'est-à-dire, les approximer de façon la plus fidèle possible par un signal discret^[3].

• Un signal est qualifié de « déterministe » si son évolution peut être exactement prédite par un modèle mathématique.

Tout signal exprimé directement de façon mathématique est donc automatiquement déterministe. Par exemple, l'évolution des feux tricolores sur la route est déterministe.

Les signaux périodiques sont en fait particulièrement déterministes car ils se répètent de façon identiques dans le temps et on peut donc prédire leur évolution facilement.

• Un signal est qualifié d'« aléatoire » si on ne peut prédire exactement ses valeurs futures

Un signal que l'on mesure avec un capteur est automatiquement aléatoire étant donné qu'il est impossible de le mesurer parfaitement sans aucun bruit.

Ceci étant dit, en pratique nous pouvons rencontrer des signaux où la part d'aléas est faible. On considère alors ce type de signal comme étant quasi-déterministe. Par exemple, un électrocardiogramme peut être considéré comme quasi-déterministe si on observe dans ce dernier une forme de répétition qui se distingue nettement du bruit de la mesure.

Il existe plusieurs opérations élémentaires utiles permettant de traiter un signal. Nous en présentons quelques-unes ci-dessous :

• Le décalage temporel qui décale le signal d’une quantité fixe sur l’axe des abscisses : ${\displaystyle x(t)\to x(t-t_{0})}$ (cas continu) ou ${\displaystyle x[n]\to x[n-n_{0}]}$.
• La réflexion qui produit un signal réfléchi par rapport à l’axe des abscisses (${\displaystyle x=0}$) : ${\displaystyle x(t)\to x(-t)}$.
• Le changement d’échelle (dilatation (${\displaystyle \beta <1}$) ou contraction (${\displaystyle \beta >1}$) du signal) selon l’axe des abscisses : ${\displaystyle x(t)\to x(\beta t)}$. 

Grâce à ces opérations, nous pouvons définir si un signal est pair: ${\displaystyle x(t)=x(-t)}$ ou ${\displaystyle x[n]=x[-n]}$  (c.à.d. il est invariant pour l’opération de réflexion) ou si un signal est impair : ${\displaystyle x(-t)=-x(t)}$ ou ${\displaystyle x[-n]=-x[n]}$ (c.à.d. l’opération de réflexion produit un changement de signe).

• R. Sepulchre, Analyse et modélisation des systèmes d'ingénieur civil ^{[réf. incomplète]}. 

• Portail de la physique
• Portail des télécommunications