Théorème de Poincaré-Bendixson — Wikipédia

Pour les articles homonymes, voir Théorèmes de Poincaré.

En mathématiques, le théorème de Poincaré-Bendixson est un résultat qualitatif sur les équations différentielles. Il concerne les équations du type (1) : ${\displaystyle {\dot {x}}=f(x)}$ où ${\displaystyle f}$ est une fonction continument dérivable, du plan réel dans lui-même et définie sur un ouvert ${\displaystyle \Omega }$. Le théorème indique que si une solution maximale^{[Note 1]} reste bornée, alors soit elle converge, soit son comportement asymptotique est celui d'une fonction périodique. Autrement dit, le plan est trop étroit pour admettre comme solutions d'équations de type (1), des trajectoires chaotiques.

Ce théorème est utilisé pour l'étude des systèmes dynamiques. Il assure que toute une classe d'équations, comme celle de Lotka-Volterra n'admet que des solutions simples (c'est-à-dire non chaotiques). En dimension 2, le chaos existe, mais pour l'obtenir il est plus simple de considérer une équation aux différences finies comme celle associée à la suite logistique. Ce résultat ne se généralise pas à la dimension trois, comme le montre le système dynamique de Lorenz. Ce résultat est aussi utile en topologie algébrique, il permet d'établir le théorème de la boule chevelue.

Ce théorème est énoncé par Henri Poincaré^[1] ; la preuve est finalement complétée par Ivar Bendixson en 1901^[2].

Dans le reste de l'article, ${\displaystyle \Omega }$ désigne un ouvert de ${\displaystyle \mathbb {R} ^{2}}$ et ${\displaystyle f}$ un champ vectoriel défini sur ${\displaystyle \Omega }$, à valeurs dans ${\displaystyle \mathbb {R} ^{2}}$ et continument différentiable. L'équation différentielle autonome nommée (1) est la suivante :

${\displaystyle (1)\quad {\frac {\mathrm {d} x}{\mathrm {d} t}}=f(x)}$.

La fonction ${\displaystyle s}$ est définie sur ${\displaystyle \mathbb {R} }$ et est une solution maximale de l'équation (1). Ici, le terme maximal^{[Note 1]} signifie que la fonction ${\displaystyle s}$ est définie sur un intervalle ${\displaystyle I}$ et qu'il n'existe aucune fonction définie sur un intervalle ${\displaystyle J}$, confondue avec ${\displaystyle s}$ sur ${\displaystyle I}$, telle que ${\displaystyle J}$ contienne strictement ${\displaystyle I}$ et qui soit solution de l'équation (1).

L'équation étudiée possède plusieurs spécificités. Tout d'abord elle est à valeurs dans un plan, elle correspond à un système de deux équations différentielles d'ordre un. Ensuite, à chaque point de la trajectoire d'une solution x(t), l'équation donne la dérivée x'(t). Ici le terme de trajectoire d'un point p désigne l'image d'une courbe intégrale passant par p^[4], ce terme est synonyme d'orbite de p^[5]. Pour imaginer la solution, on peut considérer une étendue d'eau dont la surface est parcourue par un courant décrit par la fonction f. Cette situation est illustrée sur la figure de droite. Les vecteurs indiquent la direction et la force du courant. Une telle fonction f est appelée un champ vectoriel.

Une solution est une courbe dont la trajectoire (c'est-à-dire l'ensemble des points qui constituent l'ensemble d'arrivée de la solution) possède en chaque point p une tangente dirigée par le vecteur f(p) du champ vectoriel. La vitesse scalaire (c'est-à-dire la norme de la dérivée pour le produit scalaire canonique) est égale à la norme du vecteur f(p) en ce point de la trajectoire. Pour reprendre la comparaison précédente, on obtient une solution en plaçant un bouchon dans l'eau. Le mouvement du bouchon, c'est-à-dire sa trajectoire ainsi que sa vitesse scalaire en chaque point, est une solution de l'équation différentielle.

L'équation est dite autonome, cela signifie que le courant ne varie pas avec le temps. Cela signifie que si l'on souhaite simuler l'équation à l'aide du bouchon, on peut le lâcher à un point p₀, voir son évolution pendant une durée t qui l'amène au point p_t, retirer le bouchon pour « aller prendre un café^[4] » et reposer le bouchon au point p_t pour simuler la fin de la trajectoire du bouchon. La pause café ne modifie pas cette trajectoire car le courant est stable.

Le bouchon peut avoir plusieurs comportements, si le courant est à l'image de celui d'un fleuve il finit par beaucoup s'éloigner. Cette configuration n'est pas celle du théorème. On suppose que la trajectoire reste dans un espace borné, comme celui d'un étang agité par un courant régulier. Le théorème indique que le bouchon peut finir par s'arrêter, c'est-à-dire qu'il s'approche de plus en plus d'un point sans courant, à l'image de l'illustration de droite. Si ce n'est pas le cas, le bouchon est pris dans un tourbillon et tourne sans cesse et, une fois le système stabilisé, chaque tour du bouchon est identique au précédent.

Pour se faire une idée intuitive de la démonstration, imaginons une solution s, qui ne converge pas et reste dans une zone bornée, à l'image de celle de frontière rouge sur la figure de gauche. L'intuition du bouchon se déplaçant à l'aide d'un courant montre que la solution ne s'arrête jamais. Autrement dit, si le bouchon est mis dans l'eau à l'instant t = 0, la solution s est définie sur R₊.

Si la trajectoire se croise, c'est qu'il existe deux valeurs t₁ et t₁ + δ telles que le bouchon soit à la même position à ces deux instants. Comme la trajectoire du bouchon ne dépend que du courant, son mouvement à partir de t₁ et à partir de t₁ + δ est exactement la même et à l'instant t₁ + 2.δ le bouchon se retrouve encore exactement au même endroit. Ce qui montre l'existence d'un cycle limite, atteint exactement au moins à partir de l'instant t₁.

Supposons maintenant que la trajectoire ne se « croise » jamais. On peut supposer qu'à partir d'un certain temps, la trajectoire est toujours parcourue dans le même sens de rotation, à l'image de la figure de gauche. Supposons de plus qu'elle « s'enroule » sur l'extérieur et chaque presque tour elle est un peu plus proche de la frontière en rouge. La trajectoire est de plus en plus coincée entre la frontière rouge et la « boucle » précédente. L'intuition indique qu'elle finit par converger vers un lacet simple, c'est-à-dire boucle sans point double. Plus la solution s voit sa trajectoire se rapprocher de cette boucle, plus sa vitesse est proche de celle qu'elle aurait si la trajectoire était exactement sur la boucle, car le courant (autrement dit la fonction f définissant l'équation) est continu. Le cycle limite est donc un peu intuitif dans ce cas là. Le même raisonnement s'applique si la solution s'enroule sur l'intérieur et non plus à l'extérieur.

Pour ne pas posséder de cycle limite, il semble nécessaire que la trajectoire change une infinité de fois de « sens de rotation ». En effet, s'il n'y avait qu'un nombre fini de modification de ce sens, à partir d'une certaine valeur de t, la trajectoire serait revenue à la situation précédentes. Ces changements de rotations sont illustrés sur la figure de droite. Comme la courbe est « coincée » dans une zone bornée et qu'elle ne peut pas se croiser, les virages imposés par l'infinité de modification du sens de rotation sont nécessairement de plus en plus « serrés ». Ils finissent même par être plus « serrés » que n'importe quelle valeur que l'on peut imposer, ce qui intuitivement signifie qu'il existe au moins un point où le courant n'est pas continu et ce qui est contraire aux hypothèses du théorème.

Un oscillateur harmonique est régi par l'équation différentielle suivante^[6], si M, B et K sont des constantes réelles (M et K sont strictement positifs et B est positif ou nul) :

${\displaystyle M{\ddot {x}}+B{\dot {x}}+Kx=0}$.

Ce système n'est pas exactement de la forme indiquée précédemment, mais si l'on choisit pour variable dépendant du temps non plus uniquement la fonction réelle x mais le couple (x, v), où v désigne la vitesse du système, on obtient :

${\displaystyle {\begin{cases}{\dot {v}}={\frac {1}{M}}\left(-Kx-Bv\right)\\{\dot {x}}=v.\end{cases}}}$

Ce système vérifie les hypothèses du théorème de Poincaré-Bendixson. Des considérations d'énergie montrent en effet que x et v sont nécessairement bornés. Si B, correspondant au coefficient d'amortissement, est nul on trouve une solution périodique de trajectoire une ellipse, dans l'espace des phases. C'est-à-dire que le couple (x, v) décrit une ellipse. Si B n'est pas nul, on trouve une trajectoire qui se stabilise, la valeur x tend vers le point d'équilibre, illustré sur la figure de gauche, et v tend vers le vecteur nul.

L'exemple précédent est particulièrement simple car linéaire et à coefficients constants. L'équation de Lotka-Volterra est à cet égard un peu plus complexe, car non linéaire. Elle correspond à une modélisation d'un système proie-prédateur, par exemple le couple lièvre-lynx dans la baie d'Hudson^[7]. Si les lynx sont nombreux, la population de lièvres finit par décroître suffisamment pour qu'à leur tour les lynx diminuent en nombres, ce qui engendre un nouveau développement des lièvres. Si x désigne l'effectif des proies, y celui des prédateurs et les lettres grecques des paramètres, l'équation s'écrit sous forme du système :

${\displaystyle {\begin{cases}{\frac {\mathrm {d} x}{\mathrm {d} t}}=x(\alpha -\beta y)\\{\frac {\mathrm {d} y}{\mathrm {d} t}}=-y(\gamma -\delta x).\end{cases}}}$

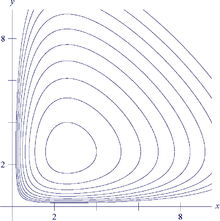
Une fois encore, les valeurs de x et de y sont nécessairement bornées. Si le nombre de lièvres augmente trop, les lynx se multiplient et la population diminue à nouveau. De même, si les lynx augmentent en trop grand nombre, les lièvres se raréfient. Cette situation n'aboutit pas toujours à un équilibre stable. Dans le cas général, on obtient des cycles à l'image de la figure de droite. En revanche, le théorème de Poincaré-Bendixson garantit que le chaos ne peut provenir d'une telle dynamique.

On trouve un premier exemple relativement proche de l'équation de Lotka-Volterra. Le facteur limitant de la population étudiée n'est pas nécessairement un prédateur, mais peut-être la population elle-même qui, si elle augmente, finit par épuiser les réserves disponibles. Un siècle avant Lotka et Voltera, Verhulst avait modélisé l'évolution de la population par l'équation différentielle suivante^[8], dont la solution est appelée fonction logistique :

${\displaystyle {\frac {\mathrm {d} x}{\mathrm {d} t}}=x(\alpha -\beta x)}$.

En elle-même, cette équation n'est pas un contre-exemple. Cependant cette équation a son équivalent avec une suite récurrente dite logistique. Elle est adaptée pour modéliser les « populations dont les générations ne se chevauchent pas »^[9]. Les arguments utilisés pour la preuve intuitive du théorème ne s'appliquent pas à une équation aux différences finies. Pour cette raison, un résultat analogue à celui du théorème de l'article n'est pas vérifié. À la différence de la fonction logistique, toujours convergente, le comportement limite de la suite logistique se présente globalement sous trois aspects, convergence, existence d'un cycle limite, mais la situation chaotique existe aussi^[10].

Il est aussi possible de construire un contre exemple en modifiant la dimension de l'espace des phases. La démonstration intuitive montre que si, au bout d'un certain temps, la trajectoire tourne toujours dans le même sens, elle se trouve coincée dans un espace de plus en plus réduit. En dimension 3, ce résultat n'est pas vrai, la trajectoire peut toujours passer « par au-dessus » ou « par en dessous ». Ce comportement se produit pour le système dynamique de Lorenz, dont l'espace des phases est de dimension trois. Le comportement limite de la trajectoire est illustré à droite. La troisième dimension rend possible une double boucle, avec une trajectoire passant de l'une à l'autre. Ce comportement n'est ni convergent ni asymptotique à une fonction périodique^[11].

La démonstration en elle-même du théorème est relativement simple, elle utilise en revanche une « machinerie^[12] » un peu lourde. Elle joue un rôle majeur dans l'analyse des systèmes dynamiques.

Le théorème de Cauchy-Lipschitz garantit l'existence et l'unicité d'une solution maximale vérifiant une condition initiale. Sous réserve d'une régularité suffisante de la fonction f, il montre l'existence de deux propriétés vérifiées par toute une fonction s satisfaisant aux hypothèses du théorème :

Une solution maximale s(t) vérifiant les hypothèses du théorème de Poincaré-Bendixson possède comme domaine de définition l'ensemble R tout entier.

Ce résultat permet d'assurer un véritable sens aux mots comportement asymptotique appliqués à s, il est en effet possible de parler de la limite de s(t) quand t tend vers l'infini. Le deuxième résultat permet de conclure sur ce comportement si s contient un point double.

Une fonction s(t) vérifiant les hypothèses du théorème de Poincaré-Bendixson et possédant un point double est périodique.

Ces deux propositions correspondent à deux assertions intuitives. Tout d'abord, on peut laisser indéfiniment le bouchon dans l'étang, rien n'arrêtera sa trajectoire. En fait, les seules choses qui pourraient l'arrêter est le fait d'être bloqué le bord de l'étang (une autre logique explique alors sa trajectoire), ou que le courant soit de plus en plus violent, à tel point que le bouchon se trouve infiniment loin en un temps fini. Ces deux configurations sont impossibles dans le cadre du théorème. La deuxième assertion est que, si le bouchon revient à un point par lequel il est déjà passé, il parcourt indéfiniment la même trajectoire.

Une manière d'étudier l'équation différentielle (1) est de considérer son flot^{[Note 1]}. C'est la fonction φ qui, à un instant t et à un point x de Ω associe le point de Ω, noté φ_t(x), correspondant à l'image de t par la courbe intégrale s vérifiant la condition de Cauchy s(0) = x. La fonction x ↦ φ_t(x) est celle qui indique ce qu'est devenu chaque point de Ω, au bout d'un laps de temps t, et la fonction t ↦ φ_t(x) est la courbe intégrale vérifiant la condition de Cauchy s(0) = x.

Dans le cas particulier du théorème de l'article, la fonction φ est définie pour toute valeur de R sur la zone qui nous intéresse. D'après le paragraphe précédent, elle vérifie de plus φ_s(φ_t(x)) = φ_s+t(x), ou encore φ_s∘φ_t = φ_s+t, ce qui lui confère une structure de groupe.

Certains sous-ensembles de Ω jouent un rôle particulier. On appelle ensemble invariant par le flot φ_t une partie S de Ω telle que pour tout réel t, φ_t(S) soit inclus dans S^[13]. Un cas particulier d'ensemble invariant par le flot est l'orbite ou encore la trajectoire d'un point x de Ω, c'est-à-dire l'image d'une courbe intégrale maximale passant par x. Dans le contexte du théorème, l'ensemble invariant qui nous intéresse est un peu différent ; il permet d'étudier le comportement asymptotique d'une courbe intégrale^[14].

Soit x un point de Ω dont la courbe intégrale maximale est définie sur R. L'ensemble ω-limite^[14] de x, noté ω(x), est l'intersection des adhérences des sections finissantes de l'image de la courbe intégrale maximale vérifiant la condition de Cauchy s(0) = x.

${\displaystyle \omega (x)=\bigcap _{t\geq 0}{\overline {\{\varphi _{s}(x)\mid s\geq t\}}}}$.

Autrement si un point y de Ω est élément de ω(x), lorsqu'il existe une suite réelle croissante (t_n) qui tend vers plus l'infini telle que φ_tn(x) admette pour limite y.

L'ensemble ω(x) possède certaines propriétés :

• Pour tout réel t, ω(x) = ω(φ_t(x)) et ω(x) est un ensemble invariant par le flot φ_t. En particulier, si y est un élément de ω(x), une courbe intégrale passant par y possède une image incluse dans ω(x). Si la trajectoire de x est à valeurs dans un compact, ω(x) est un connexe compact non vide^[4].

La suite de l'article montre que comprendre le comportement asymptotique de x revient à comprendre le comportement de la courbe intégrale de y, si y est un point de ω(x).

Démonstration

• Si t est un nombre réel, alors ω(x) = ω(φ_t(x)) :

Cette proposition est simple à démontrer, il suffit de comparer les définitions des deux ensembles :

${\displaystyle \omega (x)=\bigcap _{\tau \geq 0}{\overline {\{\varphi _{s}(x)\mid s\geq \tau \}}}\quad \omega (\varphi _{t}(x))=\bigcap _{\tau \geq 0}{\overline {\{\varphi _{s}(x)\mid s\geq t+\tau \}}}\quad {\text{car}}\quad \varphi _{t+\tau }=\varphi _{t}\circ \varphi _{\tau }}$.

• ω(x) est invariant par l'action du flot φ_t :

Soit y un élément de ω(x), il existe une suite réelle croissante (t_n), de limite plus l'infini, tel que la suite (φ_tn(x)) admette pour limite y. La fonction φ de R×K dans K est une fonction continue^{[Note 1]}, donc la suite (φ_t(φ_tn(x))) admet pour limite φ_t(y). La structure du groupe du flot montre que la suite s'écrit encore (φ_t+tn(x)) et la suite (t + t_n) est bien une suite croissante de limite plus l'infini.

• ω(x) est un compact non vide :

Ceci résulte du théorème des compacts emboités, puisque ω(x) est l'intersection des {φ_s(x) | s ≥ n}, qui forment une suite décroissante de parties non vides du compact K, fermées donc compactes.

• ω(x) est un connexe :

En effet, les compacts {φ_s(x) | s ≥ n} sont connexes (comme adhérences de connexes), donc (propriété des suites décroissantes de compacts) leur intersection ω(x) aussi.

Cette proposition n'est pas nécessairement vraie si ω(x) n'est pas compact. La raison est illustrée sur la figure de droite. Si la trajectoire est une spirale aplatie, dont les côtés s'éloignent à l'infini, l'ensemble ω-limite se réduit à deux droites, illustrées en rouge. Il n'est donc pas connexe.

• Portail de l'analyse