Système cristallin trigonal — Wikipédia

Représentation d'une maille rhomboédrique dans un réseau hexagonal.

En cristallographie, le système cristallin trigonal est l'une des sept catégories de classement des cristaux dans l'espace tridimensionnel sur la base de leurs symétries morphologiques et de leurs propriétés physiques. Il regroupe les cristaux de symétries 3, 3, 32, 3m et 3m, selon la notation d'Hermann-Mauguin. C'est le seul système cristallin de l'espace tridimensionnel qui repose sur deux réseaux de Bravais distincts : le système réticulaire hexagonal, dont la maille a des paramètres cristallins a = b (c indépendant) avec α = β = 90° et γ = 120°, et le système réticulaire rhomboédrique, dont la maille à les paramètres cristallins a = b = c, avec les angles α = β = γ ≠ 90°. Le système réticulaire hexagonal étant également sous-jacent au système cristallin hexagonal, ce dernier forme, avec le système cristallin trigonal, la famille cristalline hexagonale.

Réseau de Bravais	Hexagonal	Rhomboédrique
Symbole de Pearson	hP	hR
Maille cristalline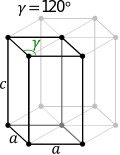

Un système cristallin est caractérisé par des éléments de symétrie caractéristiques, ici un axe de rotation ternaire, 3 ou 3.

Liste des groupes ponctuels

Ilménite du mont Saint-Hilaire, au Québec.

Les cinq groupes ponctuels qui se trouvent dans ce système cristallin sont listés ci-dessous, suivis par leurs représentations dans la notation internationale de Hermann-Mauguin et celle de Schonflies, avec quelques exemples de minéraux et les 25 groupes d'espace associés (7 ont une maille élémentaire rhomboédrique (R) et 18 une maille élémentaire hexagonale (P)).

N°	Groupe ponctuel					Exemples	Groupe d'espace
N°	Classe (Groth)	Intl	Schoenflies	Orbifold	Coxeter	Exemples	Hexagonal	Rhomboédrique
143-146	Trigonale-pyramidale	3	C₃	33	[3]⁺	Carlinite, Jarosite	P3, P3₁, P3₂	R3
147-148	Rhomboédrique	3	S₆	3×	[2⁺,6⁺]	Dolomite, Ilménite	P3	R3
149-155	Trigonale-trapézoédrique	32	D₃	223	[2,3]⁺	Abhurite, Quartz, Cinabre	P312, P321, P3₁12, P3₁21, P3₂12, P3₂21	R32
156-161	Ditrigonale-pyramidale	3m	C_3v	*33	[3]	Schorl, Cérite, Tourmaline, Alunite, Tantalate de lithium	P3m1, P31m, P3c1, P31c	R3m, R3c
162-167	Ditrigonale-scalénoédrique	3m	D_3d	2*3	[2⁺,3]	Antimoine, Hématite, Corindon, Calcite	P31m, P31c, P3m1, P3c1	R3m, R3c

Famille cristalline hexagonale

Jarosite de Cuevas del Almanzora, en Andalousie (Espagne).

La famille cristalline hexagonale est constituée des douze groupes ponctuels tels qu'au moins un de leurs groupes d'espace a le réseau hexagonal comme réseau sous-jacent, et est l'union du système cristallin hexagonal et du système cristallin trigonal^[1].

Famille cristalline	Hexagonale
Système cristallin	Hexagonal	Trigonal
Réseau de Bravais	Hexagonal		Rhomboédrique
Symbole de Pearson	hP		hR
Maille cristalline	Hexagonale		Rhomboédrique
Exemples	Béryl	Quartz $α$	Dolomite

52 groupes d'espace lui sont associés, qui sont exactement ceux dont le réseau de Bravais est soit hexagonal soit rhomboédrique.

Système cristallin	Symétries minimales requises	Groupes ponctuels	Groupes d'espace	Réseaux de Bravais	Système réticulaire
Trigonal	1 axe de rotation d'ordre 3	5	7	1	Rhomboédrique
Trigonal	1 axe de rotation d'ordre 3	5	18	1	Hexagonal
Hexagonal	1 axe de rotation d'ordre 6	7	27	1	Hexagonal

Notes et références

↑ (en) Cornelius S. Hurlbut et Cornelis Klein, Manual of Mineralogy, New York/Chichester/Brisbane etc., J. Wiley and sons, 1985, 20^e éd., 596 p. (ISBN 0-471-80580-7), p. 78-89.

Voir aussi

Articles connexes

Bibliographie

(en) Cornelius S. Hurlbut et Cornelis Klein, Manual of Mineralogy, New York/Chichester/Brisbane etc., J. Wiley and sons, 1985, 20^e éd., 596 p. (ISBN 0-471-80580-7), p. 78-89.

Famille cristalline	Triclinique	Monoclinique	Orthorhombique	Tétragonale	Hexagonale			Cubique

Classement des cristaux tridimensionnels
Système cristallin	Triclinique	Monoclinique	Orthorhombique	Tétragonal	Trigonal		Hexagonal	Cubique
Système réticulaire	Triclinique	Monoclinique	Orthorhombique	Tétragonal	Rhomboédrique	Hexagonal		Cubique
Paramètres cristallins	a ≠ b ≠ c α ≠ β ≠ γ ≠ 90°	a ≠ b ≠ c α = γ = 90° ≠ β	a ≠ b ≠ c α = β = γ = 90°	a = b ≠ c α = β = γ = 90°	a = b = c α = β = γ ≠ 90°	a = b α = β = 90° ; γ = 120°		a = b = c α = β = γ = 90°

[1] (en) Cornelius S. Hurlbut et Cornelis Klein, Manual of Mineralogy, New York/Chichester/Brisbane etc., J. Wiley and sons, 1985, 20^e éd., 596 p. (ISBN 0-471-80580-7), p. 78-89.

[1]