Aristarco di Samo

Aristarco di Samo (in greco antico: Ἀρίσταρχος ὁ Σάμιος?, Arístarchos ho Sámios; Samo, 310 a.C. circa – 230 a.C. circa) è stato un astronomo greco antico.

Biografia
[modifica | modifica wikitesto]Nato a Samo, una delle maggiori isole in prossimità della costa della Ionia, Aristarco studiò ad Alessandria, dove ebbe come maestro Stratone di Lampsaco.
Per le sue teorie si diceva che meritasse la condanna per empietà, come riporta Giacomo Leopardi nella sua Storia dell'astronomia:
«Altro astronomo greco fu Aristarco, vissuto, come credesi, verso il 264 avanti Gesù Cristo, benché considerevolmente più antico lo facciano il Fromondo e il Simmler presso il Vossio, ripresi però dal Fabricio. Di lui fecer menzione Vitruvio, Tolomeo e Varrone presso Gellio nel quale, in luogo di Aristide Samio, è da leggersi Aristarco. Egli determinò la distanza del Sole dalla Terra, che egli credé 19 volte maggiore di quella della Terra medesima dalla Luna e trovò la distanza della Terra dalla Luna, di 56 semidiametri del nostro globo. Credette che il diametro del sole fosse non più che 6 o 7 volte maggiore di quello della Terra e che quello della Luna fosse circa un terzo di quello della Terra medesima. Fu dogma di Aristarco il moto della Terra, ed egli, per tale opinione, reputossi da Cleante reo di empietà, quasi avesse turbato il riposo dei Lari e di Vesta. Sembra che Plutarco asserisca essere stato Cleante e non Aristarco il fautore del moto della Terra, così leggesi nel suo libro De facie in orbe Lunae.»
L'ultima affermazione del giovanissimo Leopardi richiede una spiegazione. In realtà il testo di Plutarco tramandato dai manoscritti era stato emendato dal filologo Aegidius Menagius (nome latinizzato di Gilles Ménage) nel XVII secolo. Nel testo dei manoscritti era scritto che Aristarco avrebbe voluto scherzosamente accusare di empietà Cleante (costui era infatti seguace del culto del Sole e allo stesso tempo contrario all'eliocentrismo). Menagius aveva emendato il testo invertendo il ruolo di accusato e accusatore, ritenendo che ad essere accusato di empietà potesse essere solo il sostenitore dell'eliocentrismo. Leopardi leggeva nei libri di storia dell'astronomia che l'eliocentrismo aveva portato ad un'accusa di empietà, ma leggeva anche l'originale testo greco di Plutarco, che sosteneva chiaramente che era stato Cleante l'accusato. Ne concluse che Cleante dovesse essere l'eliocentrista[1]. L'accusa di empietà quindi fu solo un gioco dialettico tra Aristarco e Cleante, ma non fu mai formulata né contro l'uno né contro l'altro[1].
Opere
[modifica | modifica wikitesto]La teoria eliocentrica
[modifica | modifica wikitesto]Astronomo e fisico, Aristarco è noto soprattutto per avere per primo introdotto una teoria astronomica nella quale il Sole e le stelle fisse sono immobili mentre la Terra ruota attorno al Sole percorrendo una circonferenza[2]. Sappiamo inoltre che Aristarco concordava con Eraclide Pontico nell'attribuire alla Terra anche un moto di rotazione diurna attorno ad un asse inclinato rispetto al piano dell'orbita intorno al Sole[3] (l'ultima ipotesi giustificava l'alternarsi delle stagioni)[4].
Dell'opera in cui Aristarco illustrava la teoria eliocentrica, ci rimangono solo pochi frammenti, costituiti da brevi citazioni di tradizione indiretta[5]. L'obiezione che gli mossero i suoi contemporanei fu per quale motivo le stelle fisse non modificassero la propria posizione reciproca nel corso dell'anno, come avrebbero dovuto fare se la Terra fosse stata in movimento. Archimede riporta che Aristarco superò l'obiezione ipotizzando che la distanza tra la Terra e le stelle fisse fosse infinitamente maggiore del raggio dell'orbita annuale terrestre[6], e in effetti è tanto maggiore da evitare ogni effetto di parallasse misurabile con gli strumenti dell'epoca (e anche delle epoche successive fino al XIX secolo). L'idea che le stelle siano ad una distanza enormemente superiore a quella del Sole è ripresa da altri autori[2] (ad esempio da Cleomede).
Secondo la testimonianza di Plutarco, mentre Aristarco proponeva l'eliocentrismo come un'ipotesi, questo era una netta convinzione per Seleuco di Seleucia[7]. La teoria eliocentrica era stata rifiutata con forza un secolo prima da Platone e dal suo allievo Aristotele, e fu respinta quattro secoli dopo Aristarco, anche da Claudio Tolomeo, le cui concezioni dominarono incontrastate la tarda antichità e il medioevo. Ha senso supporre però che la teoria di Aristarco fosse accettata per i primi secoli, dato che Plinio il Vecchio[8] e Seneca[9] si riferiscono al moto retrogrado dei pianeti come a un fenomeno ottico e non reale, concezione più in linea con l'eliocentrismo che con il geocentrismo.
Dimensioni e distanze del Sole e della Luna
[modifica | modifica wikitesto]L'unica opera pervenuta di Aristarco è il breve trattato Sulle dimensioni e distanze del Sole e della Luna[10], nel quale stima la grandezza del Sole e della Luna e calcola le relative distanze dalla Terra.
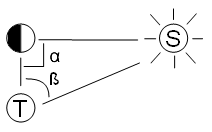
Quando la Luna è in quadratura, ossia è illuminata per metà, essa, con la Terra e il Sole, forma il triangolo rettangolo mostrato in figura. Misurando in tale condizione l'angolo β compreso tra la direzione Terra-Sole e la direzione Terra-Luna è possibile calcolare il rapporto tra le loro distanze mediante ragionamenti di tipo geometrico. Il problema risolto da Aristarco, di calcolare (o meglio, stimare sia per eccesso che per difetto) il rapporto tra i cateti di un triangolo del quale si conoscono gli angoli, equivale in termini attuali a calcolare, o stimare, la tangente trigonometrica di un angolo. L'opera di Aristarco può pertanto essere considerata una delle prime opere di trigonometria[2].
Aristarco stimò il rapporto tra le distanze del Sole e della Luna come compreso tra 18 e 20, mentre il rapporto tra le distanze medie è in realtà circa 400. Le stime di Aristarco sono correttamente dedotte dal valore da lui assunto per l'angolo Sole-Terra-Luna all'atto della quadratura, ma l'angolo era stato misurato con scarsa precisione. La grandezza abnorme dell'errore è dovuta a due cause principali. In primo luogo Aristarco dovette calcolare la tangente di un angolo molto vicino a un angolo retto, molto vicino cioè al valore nel quale la tangente diverge. In queste condizioni un errore relativamente piccolo sull'angolo si traduce necessariamente in un errore enormemente maggiore sulla tangente. Inoltre per stimare con accuratezza l'angolo che interessava Aristarco occorre riconoscere l'effettiva quadratura con una precisione difficilmente raggiungibile ad occhio nudo. Basta un errore di poche ore sull'istante in cui la quadratura ha luogo perché l'errore sull'angolo si traduca in un errore enorme sulla sua tangente[6].
Il metodo di Aristarco permette comunque di stimare la tangente di qualsiasi angolo e questo è probabilmente il maggior valore matematico della sua opera.
Ad Aristarco sono stati intitolati il cratere lunare Aristarchus e l'asteroide 3999 Aristarchus[11].
Note
[modifica | modifica wikitesto]- ^ a b Lucio Russo, Sulla presunta accusa di empietà ad Aristarco di Samo, in "Quaderni urbinati di cultura classica", 1996, pp. 1-3, su (PDF) Sulla presunta accusa di empietà ad Aristarco di Samo | Lucio Russo - Academia.edu Fonte]
- ^ a b c Vincenzo Zappalà, Aristarco di Samo e la teoria eliocentrica Fonte Url Consultato il 23.8. 2015.
- ^ Andrea Frova, Il Cosmo e il Buondio. Dialogo su astronomia, evoluzione e mito (Aristarco. il Copernico dell'Antichità), Milano, R.C.S. Libri, 2009 Fonte.
- ^ Francesco Porro de Somenzi, Aristarco di Samo, in Enciclopedia Italiana, Vol IV, Roma 1929 Aristarco di Samo.
- ^ La più importante delle quali è di Archimede nell'Arenario.
- ^ a b James Evans, Aristarchus of Samos, in Encyclopaedia Britannica [1].
- ^ Neugebauer, History of Ancient Mathematical Astronomy (1975), p. 697.
- ^ Naturalis Historia, II, 70.
- ^ Naturales Quaestiones, VII, 25, 6–7.
- ^ Περί μεγετῶν καὶ ἀποστεμάτων ἡλίου καὶ σελήνης.
- ^ NNBD, Aristarchus of Samos Fonte
Bibliografia
[modifica | modifica wikitesto]- (EN) Sir ThomasL. Heath, Aristarchus of Samos - The Ancient Copernicus, A history of Greek astronomy to Aristarchus . Oxford, Clarendon, 1913; rist. New York, Dover, 1981. (contiene testo greco e traduzione inglese del trattato Sulle dimensioni e distanze del Sole e della Luna).
- Osvaldo Rea, Nautilus, l'enigma dell'impero, Pompei [Palestra Grande], ISBN 88-901473-9-3
- Andrea Frova, Il Cosmo e il Buondio. Dialogo su astronomia, evoluzione e mito (Aristarco. il Copernico dell'Antichità), R.C.S. Libri S.p.A. - Milano.2009
- Raffaele Ruggiero, La scuola di Aristarco, Fasano, Ed. Schena, 1998.
- Vincenzo Zappalà, Aristarco di Samo e la teoria eliocentrica, Astronomia.com
- Lucio Russo, Sulla presunta accusa di empietà ad Aristarco di Samo, Quaderni urbinati di cultura classica, JSTOR (Digital library of academic journals, books, and primary sources) 1996
- Francesco Porro de Somenzi, ARISTARCO di Samo, in Enciclopedia Italiana, IV, Roma, Istituto dell'Enciclopedia Italiana, 1929.
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikisource contiene una pagina dedicata a Aristarco di Samo
Wikisource contiene una pagina dedicata a Aristarco di Samo Wikiquote contiene citazioni di o su Aristarco di Samo
Wikiquote contiene citazioni di o su Aristarco di Samo Wikimedia Commons contiene immagini o altri file su Aristarco di Samo
Wikimedia Commons contiene immagini o altri file su Aristarco di Samo
Collegamenti esterni
[modifica | modifica wikitesto]- Aristarco di Samo, su Treccani.it – Enciclopedie on line, Istituto dell'Enciclopedia Italiana.
- Francesco Porro de Somenzi, ARISTARCO di Samo, in Enciclopedia Italiana, Istituto dell'Enciclopedia Italiana, 1929.
- Aristarco di Samo, in Dizionario di filosofia, Istituto dell'Enciclopedia Italiana, 2009.
- Aristarco di Samo, in Enciclopedia della Matematica, Istituto dell'Enciclopedia Italiana, 2013.
- (EN) James Evans, Aristarchus of Samos, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Aristarco di Samo, su MacTutor, University of St Andrews, Scotland.
- (EN) Opere di Aristarco di Samo, su Open Library, Internet Archive.
- (EN) Aristarco di Samo, su Goodreads.
| Controllo di autorità | VIAF (EN) 79398695 · ISNI (EN) 0000 0001 1798 0082 · SBN BVEV019633 · BAV 495/14670 · CERL cnp00979569 · LCCN (EN) n82068128 · GND (DE) 118645714 · BNE (ES) XX4421307 (data) · BNF (FR) cb125157746 (data) · J9U (EN, HE) 987007277977605171 |
|---|


 French
French Deutsch
Deutsch