Bipiramide triangolare elongata

Bipiramide triangolare elongata
Tipo	Solido di Johnson J13 - J14 - J15
Forma facce	6 Triangoli 3 Quadrati
Nº facce	9
Nº spigoli	15
Nº vertici	8
Incidenza dei vertici	2(33) 6(32.42)
Gruppo di simmetria	D3h, [3,2], (*322)
Gruppo rotazionale	D3, [3,2]+, (322)
Duale	Bitronco di piramide
Proprietà	Convessità
Politopi correlati
Poliedro duale
Sviluppo piano
Manuale

In geometria solida, la bipiramide triangolare elongata è un solido di 9 facce che può essere costruito, come intuibile dal suo nome, allungando una bipiramide triangolare attraverso l'aggiunta di un prisma triangolare tra le sue due metà congruenti.

Nel caso in cui tutte le sue facce siano poligoni regolari, la bipiramide triangolare elongata diventa uno dei 92 solidi di Johnson, in particolare quello indicato come J₁₄, ossia un poliedro strettamente convesso avente come facce dei poligoni regolari ma comunque non appartenente alla famiglia dei poliedri uniformi.^[1]

Considerando una bipiramide triangolare elongata avente come facce dei poligoni regolari aventi lato di lunghezza ${\displaystyle a}$, le formule per il calcolo del volume ${\displaystyle V}$, della superficie ${\displaystyle A}$ e dell'altezza ${\displaystyle h}$ risultano essere:

${\displaystyle V={\frac {a^{3}}{12}}(2{\sqrt {2}}+3{\sqrt {3}})\approx 0,668715\ldots a^{3};}$

${\displaystyle A={\frac {3a^{2}}{2}}(2+{\sqrt {3}})\approx 5,59808\ldots a^{2};}$

${\displaystyle h={\frac {3+2{\sqrt {6}}}{3}}a\approx 2,63299\ldots a.}$

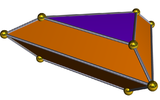
Il poliedro duale di una bipiramide triangolare elongata è un bitronco di piramide, detto anche bitronco triangolare, il quale ha 8 facce: sei trapezoidali e due triangolari.

Poliedro duale	Sviluppo piano del duale

• (EN) Eric W. Weisstein, Bipiramide triangolare elongata, su MathWorld, Wolfram Research.

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica