Buco nero



In astrofisica, un buco nero è un corpo celeste con un campo gravitazionale così intenso (ovvero, una regione dello spaziotempo con una curvatura talmente alta) che dal suo interno non può uscire nulla, nemmeno la luce[3] essendo la velocità di fuga superiore a c.
Il buco nero è il risultato di implosioni di masse sufficientemente elevate. La gravità domina su qualsiasi altra forza, determinando un collasso gravitazionale che tende a concentrare lo spaziotempo in un punto[4] al centro della regione, dove è teorizzato uno stato della materia di curvatura tendente a infinito e volume tendente a zero chiamato singolarità, con caratteristiche sconosciute ed estranee alle leggi della relatività generale. Il limite del buco nero è definito orizzonte degli eventi, regione che ne delimita in modo peculiare i confini osservabili.
Per le suddette proprietà, il buco nero non è osservabile direttamente. La sua presenza si rivela solo indirettamente mediante i suoi effetti sullo spazio circostante: le interazioni gravitazionali con altri corpi celesti e le loro emissioni, le irradiazioni principalmente elettromagnetiche della materia catturata dal suo campo di forza.
Nel corso dei decenni successivi alla pubblicazione della relatività generale, base teorica della loro esistenza, vennero raccolte numerose osservazioni interpretabili, pur non sempre univocamente, come prove della presenza di buchi neri, specialmente in alcune galassie attive e sistemi stellari di binarie X.[5] L'esistenza di tali oggetti è oggi definitivamente dimostrata e via via ne vengono individuati di nuovi con massa molto variabile, da valori di circa 5 masse solari fino a miliardi.
Il termine "buco nero" fu coniato dal fisico John Archibald Wheeler, che lo utilizzò a partire dal 1967 in un suo discorso a seguito del suggerimento di uno spettatore mai identificato.[6]
Storia
[modifica | modifica wikitesto]Nella fisica classica, basandosi sui principi della dinamica, era stata teorizzata nel XVIII secolo la possibilità che un corpo avesse una massa così grande da non consentire nemmeno alla luce di superare la velocità di fuga, ragione per cui tale corpo sarebbe risultato invisibile. Nel 1783 lo scienziato inglese John Michell suggerì in una lettera a Henry Cavendish (successivamente pubblicata nei rendiconti della Royal Society[7]) che la velocità di fuga da un corpo celeste potrebbe risultare superiore alla velocità della luce, dando luogo a quella che egli chiamò una "stella oscura" (dark star). Nel 1798 Pierre-Simon de Laplace riportò quest'idea nella prima edizione del suo Traité de mécanique céleste.
Da un punto di vista relativistico, il concetto di buco nero venne teorizzato dal fisico Karl Schwarzschild nel 1916, solo un anno dopo la pubblicazione della teoria della relatività generale. Nella relatività generale il campo gravitazionale viene descritto come deformazione dello spaziotempo causata da un oggetto molto massiccio, e la velocità della luce è una costante limite. Esplorando alcune soluzioni alle equazioni della teoria, Schwarzschild calcolò che un corpo ipoteticamente dotato di altissima densità produrrebbe nelle sue vicinanze una deformazione tale che la luce in allontanamento da esso tenderebbe a subire uno spostamento verso il rosso gravitazionale infinito. Il concetto teorizzato da Schwarzschild dipende dalla densità dell'oggetto, in astratto cioè si potrebbe applicare a un qualsiasi oggetto il cui volume fosse estremamente piccolo rispetto alla sua massa - anche se, nella realtà, non è noto alcun mezzo che possa fornire a un oggetto con massa piccola l'energia necessaria per concentrare a tal punto la materia: l'unica forza nota nell'universo in grado di sviluppare una tale intensità è la forza di gravità, in presenza di una grande quantità di materia.
I buchi neri secondo la relatività generale
[modifica | modifica wikitesto]Nel 1915 Albert Einstein sviluppò la sua teoria della relatività generale, avendo in precedenza dimostrato che la forza gravitazionale influenza la luce. Solo pochi mesi dopo, Karl Schwarzschild trovò una soluzione per le equazioni di campo di Einstein, che descrive il campo gravitazionale di un punto materiale e di una massa sferica. Pochi mesi dopo Schwarzschild morì e Johannes Droste, uno studente di Hendrik Lorentz, diede in modo indipendente la stessa soluzione, approfondendone le proprietà. Questa soluzione ha una caratteristica il cui significato fisico sembrò in un primo tempo incomprensibile: quando la coordinata radiale tende a uno specifico valore, detto raggio di Schwarzschild, alcune componenti della metrica tendono a un valore infinito. La natura di questa singolarità, localizzata su una superficie che fu poi chiamata orizzonte degli eventi, all’inizio non fu compresa pienamente. Nel 1924, Arthur Eddington dimostrò che la singolarità cessava di esistere con un cambiamento di coordinate (vedi coordinate Eddington-Finkelstein), tuttavia si dovette aspettare fino al 1933, quando Georges Lemaître si rese conto che quella in corrispondenza del raggio di Schwarzschild era una singolarità del sistema di coordinate, non una singolarità della metrica dello spaziotempo. Tuttavia, una vera singolarità della metrica di Schwarzschild (indipendente dalle coordinate) è presente nel centro di simmetria della soluzione.[8]
Nel 1931 Subrahmanyan Chandrasekhar calcolò, utilizzando la relatività speciale, che un corpo non rotante di elettroni-materia degenere, al di sopra di un certo limite di massa (ora chiamato il limite di Chandrasekhar di 1,4 masse solari) non ha soluzioni stabili.[9] I suoi argomenti furono contestati da molti contemporanei come Eddington e Lev Landau, i quali sostenevano che qualche forza ancora sconosciuta avrebbe impedito il collasso del corpo.[10] Questa teoria era in parte corretta: una nana bianca leggermente più massiccia rispetto al limite di Chandrasekhar collasserà in una stella di neutroni,[11] la quale è essa stessa stabile a causa del principio di esclusione di Pauli. Ma nel 1939, Robert Oppenheimer e altri previdero che le stelle di neutroni con massa pari a circa tre volte il Sole (il limite di Tolman-Oppenheimer-Volkoff) sarebbero collassate in buchi neri per le ragioni presentate da Chandrasekhar, e conclusero che nessuna legge fisica sarebbe intervenuta per fermare il collasso di alcune di queste.[12] Oppenheimer e i suoi coautori interpretarono la singolarità ai confini del raggio di Schwarzschild come la superficie di una bolla concentrata di materia in cui il tempo può rallentare e addirittura fermarsi. Questa conclusione è valida dal punto di vista di un osservatore esterno, mentre non lo è per un osservatore in caduta nel buco. A causa di questa proprietà, le stelle collassate sono chiamate "stelle congelate",[13] perché un osservatore esterno vedrebbe la superficie della stella congelata nel tempo, nel momento stesso in cui il suo collasso la portasse all'interno del raggio di Schwarzschild.
Poco dopo la formulazione della relatività generale da parte di Albert Einstein, risultò che la soluzione delle equazioni di Einstein (in assenza di materia) che rappresenta un campo gravitazionale statico e a simmetria sferica (la soluzione di Karl Schwarzschild, che corrisponde al campo gravitazionale centrale simmetrico della gravità newtoniana) implica l'esistenza di un confine ideale, detto orizzonte degli eventi, caratterizzato dal fatto che qualunque cosa lo oltrepassi, attratta dal campo gravitazionale, non sarà più in grado di tornare indietro. Poiché neppure la luce riesce ad attraversare l'orizzonte degli eventi dall'interno verso l'esterno, la regione interna all'orizzonte si comporta a tutti gli effetti come un buco nero.
Poiché la soluzione di Schwarzschild descrive il campo gravitazionale nel vuoto, essa rappresenta esattamente il campo gravitazionale all'esterno di una distribuzione di massa con simmetria sferica: un buco nero potrebbe essere teoricamente prodotto da un corpo celeste massiccio solo se questo avesse densità tale da essere interamente contenuto all'interno dell'orizzonte degli eventi (se, cioè, il corpo celeste avesse raggio inferiore al raggio di Schwarzschild corrispondente alla sua massa totale). Si pose dunque l'interrogativo se una tale densità possa essere raggiunta come effetto del collasso gravitazionale di una data distribuzione di materia. Lo stesso Einstein (al quale la "singolarità" trovata da Schwarzschild nella sua soluzione appariva come una pericolosa inconsistenza nella teoria della relatività generale) discusse questo punto in un lavoro del 1939, concludendo che per raggiungere una simile densità le particelle materiali avrebbero dovuto superare la velocità della luce, in contrasto con la relatività ristretta:
«The essential result of this investigation is a clear understanding as to why the "Schwarzschild singularities" do not exist in physical reality.»
«Il risultato fondamentale di questo studio è la chiara comprensione del perché le "singolarità di Schwarzschild" non esistono nella realtà fisica.»
In realtà Einstein aveva basato i suoi calcoli sull'ipotesi che i corpi che collassano orbitino intorno al centro di massa del sistema, ma nello stesso anno Robert Oppenheimer e H. Snyder[15] mostrarono che la densità critica può essere raggiunta quando le particelle collassano radialmente. Successivamente anche il fisico indiano A. Raychaudhuri mostrò che la situazione ritenuta da Einstein non fisicamente realizzabile è, in realtà, perfettamente compatibile con la relatività generale:
«A nonstatic solution of the Einstein gravitational equations representing a spherically symmetric cluster of radially moving particles in an otherwise empty space is obtained. While it has been presumed by Einstein that the Schwarzschild singularity is physically unattainable as matter cannot be concentrated arbitrarily, the present solution seems to show that there is no theoretical limit to the degree of concentration, and that the Schwarzschild singularity has no physical reality as it occurs only in some particular coordinate systems.»
«[In questo lavoro] si ottiene una soluzione non statica delle equazioni gravitazionali di Einstein che rappresenta un aggregato, dotato di simmetria sferica, di particelle che si muovono radialmente in uno spazio vuoto. Benché Einstein abbia ritenuto che la singolarità di Schwarzschild sia fisicamente irraggiungibile, poiché la materia non può essere concentrata arbitrariamente, la presente soluzione sembra dimostrare che non vi è un limite teorico al grado di concentrazione, e che la singolarità di Schwarzschild non ha significato fisico in quanto compare solo in particolari sistemi di coordinate.»
In altri termini, l'orizzonte degli eventi non è una reale singolarità dello spazio-tempo (nella soluzione di Schwarzschild l'unica vera singolarità geometrica è collocata nell'origine delle coordinate), ma ha comunque la caratteristica fisica di poter essere attraversato solo dall'esterno verso l'interno. In accordo con queste considerazioni teoriche numerose osservazioni astrofisiche sono state fatte risalire alla presenza di buchi neri che attraggono materia circostante.[17] Secondo alcuni modelli, potrebbero esistere buchi neri privi di singolarità, dovuti a stati della materia più densi di una stella di neutroni, ma non al punto di generare una singolarità.
Secondo le teorie attualmente considerate, un buco nero può formarsi solamente da una stella che abbia una massa superiore a 2,5 volte circa quella del Sole, come conseguenza del Limite di Tolman-Oppenheimer-Volkoff, anche se a causa dei vari processi di perdita di massa subiti dalle stelle al termine della loro vita occorre che la stella originaria sia almeno dieci volte più massiccia del Sole. I numeri citati sono meramente indicativi, in quanto dipendono dai dettagli dei modelli utilizzati per prevedere l'evoluzione stellare e, in particolare, dalla composizione chimica iniziale della nube di gas che ha dato origine alla stella in questione. Non è esclusa la possibilità che un buco nero possa avere origine non stellare, come si suppone ad esempio per i cosiddetti buchi neri primordiali.
Proprietà e struttura
[modifica | modifica wikitesto]
In astrofisica, il teorema dell'essenzialità[18] (in inglese no hair theorem) postula che tutte le soluzioni del buco nero nelle equazioni di Einstein-Maxwell sulla gravitazione e l'elettromagnetismo nella relatività generale possano essere caratterizzate solo da tre parametri classici esternamente osservabili: massa, carica elettrica e momento angolare.[19] Tutte le altre informazioni riguardanti la materia di cui è formato un buco nero o sulla materia che vi sta cadendo dentro "spariscono" dietro il suo orizzonte degli eventi e sono dunque permanentemente inaccessibili agli osservatori esterni (vedi anche il paradosso dell'informazione del buco nero). Due buchi neri che condividano queste stesse proprietà, o parametri, secondo la meccanica classica sono indistinguibili.
Queste proprietà sono speciali perché sono visibili dall'esterno di un buco nero. Ad esempio, un buco nero carico respinge un altro con la stessa carica, proprio come qualsiasi altro oggetto carico. Allo stesso modo, la massa totale all'interno di una sfera contenente un buco nero può essere trovata utilizzando l'analogo gravitazionale della legge di Gauss, la massa ADM, lontano dal buco nero.[20] Parimenti, il momento angolare può essere misurato da lontano usando l'effetto di trascinamento del campo gravitomagnetico.
Quando un oggetto cade in un buco nero, qualsiasi informazione circa la forma dell'oggetto o della distribuzione di carica su di essa è uniformemente distribuita lungo l'orizzonte del buco nero, e risulta irrimediabilmente persa per l'osservatore esterno. Il comportamento dell'orizzonte in questa situazione è un sistema dissipativo che è strettamente analogo a quello di una membrana elastica conduttiva con attrito e resistenza elettrica - il paradigma della membrana.[21] Questa congettura è diversa da altre teorie di campo come l'elettromagnetismo, che non ha attriti o resistività a livello microscopico, perché sono reversibili nel tempo. Dato che un buco nero alla fine raggiunge la stabilità con solo tre parametri, non c'è modo per evitare di perdere informazioni sulle condizioni iniziali: i campi gravitazionali ed elettrici di un buco nero danno pochissime informazioni su ciò che è stato risucchiato.
L'informazione persa comprende ogni quantità che non può essere misurata lontano dall'orizzonte del buco nero, inclusi numeri quantici approssimativamente conservati, come il totale del numero barionico e leptonico. Questo comportamento è così sconcertante che è stato chiamato il paradosso dell'informazione del buco nero.[22][23]
Proprietà fisiche
[modifica | modifica wikitesto]I buchi neri più semplici hanno una massa, ma non carica elettrica né momento angolare. Questi buchi neri sono spesso indicati come buchi neri di Schwarzschild dopo che Karl Schwarzschild scoprì questa soluzione nel 1916.[24] Secondo il teorema di Birkhoff, è l'unica soluzione di vuoto sfericamente simmetrica.[25] Ciò significa che non vi è differenza osservabile tra il campo gravitazionale di un buco nero e di un qualsiasi altro oggetto sferico della stessa massa. La convinzione popolare di un buco nero capace di "risucchiare ogni cosa" nel suo ambiente quindi è corretta solo in prossimità dell'orizzonte di un buco nero; a distanza da questo, il campo gravitazionale esterno è identico a quello di qualsiasi altro organismo della stessa massa.[26] Esistono anche soluzioni che descrivono i buchi neri più generali. I buchi neri carichi sono descritti dalla metrica di Reissner-Nordström, mentre la metrica di Kerr descrive un buco nero rotante. La soluzione più generale di un buco nero stazionante conosciuta è la metrica di Kerr-Newman, che descrive un buco nero sia con carica sia con momento angolare.[27] Mentre la massa di un buco nero può assumere qualsiasi valore positivo, la carica e il momento angolare sono vincolati dalla massa. In unità di Planck, la carica elettrica totale Q e il momento angolare totale J sono tenuti a soddisfare:
per un buco nero di massa M. I buchi neri che soddisfano questa disuguaglianza sono detti estremali. Esistono soluzioni delle equazioni di Einstein che violano questa disuguaglianza, ma che non possiedono un orizzonte degli eventi. Queste soluzioni sono le cosiddette singolarità nude che si possono osservare dal di fuori, e, quindi, sono considerate non-fisiche. L'ipotesi della censura cosmica esclude la formazione di tali singolarità, quando vengono create attraverso il collasso gravitazionale della materia realistica.[28] Questa ipotesi è supportata da simulazioni numeriche.[29] A causa della relativamente grande forza elettromagnetica, i buchi neri formatisi dal collasso di stelle sono tenuti a mantenere la carica quasi neutra della stella. La rotazione, tuttavia, dovrebbe essere una caratteristica comune degli oggetti compatti. Il buco nero binario a raggi X GRS 1915 105[30] sembra avere un momento angolare vicino al valore massimo consentito.
| Classe | Massa | Raggio |
|---|---|---|
| Buco nero supermassiccio | ~106–109 MSole | ~0.001–400 AU |
| Buco nero di massa intermedia | ~103 MSole | ~103 km ≈ RPlutone[31] |
| Buco nero stellare | ~3-30 MSole | ~30 km |
| Micro buco nero | fino a ~MLuna | fino a ~0,1 mm |
I buchi neri sono comunemente classificati in base alla loro massa, indipendente del momento angolare J o carica elettrica Q. La dimensione di un buco nero, come determinata dal raggio dell'orizzonte degli eventi, o raggio di Schwarzschild, è approssimativamente proporzionale alla massa M tramite:
dove rsh è il raggio di Schwarzschild e MSole è la massa del sole.[32] Questa relazione è esatta solo per i buchi neri con carica e momento angolare nulli, mentre per i buchi neri più generali può variare fino a un fattore di 2.
Orizzonte degli eventi
[modifica | modifica wikitesto]Caratteristica distintiva dei buchi neri è la comparsa di un orizzonte degli eventi attorno al baricentro della loro massa: si tratta di una superficie geometricamente sferica e chiusa (con apparente superficie materiale rispetto ad osservatori esterni) che ne circonda il nucleo massiccio, delimitando la regione spazio-temporale dalla quale non può uscire o venir emesso alcun segnale né alcuna quantità di materia. L'orizzonte può solo essere raggiunto e attraversato nella direzione del centro del buco nero, non in senso opposto; questo produce il costante mantenimento o un potenziale aumento della massa del buco nero che, in lunghissimo periodo, potrebbe venir destabilizzato solo dalla teorica radiazione di Hawking.
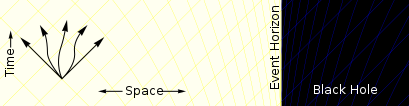
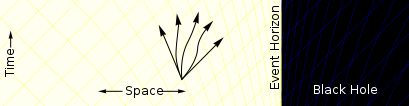
Essendo la deformazione dello spazio-tempo all'interno dell'orizzonte degli eventi tale che la velocità di fuga è uguale o superiore a c,[33] osservatori esterni non possono ottenere informazioni su eventi compresi entro i suoi confini e ciò ne rende impossibile qualsiasi verifica diretta.[34] Per osservatori fuori da tale influenza gravitazionale, come prescrive la relatività generale, orologi vicini al buco nero risultano procedere più lentamente rispetto a quelli lontani da esso.[35]
A causa di questo effetto, detto dilatazione temporale gravitazionale, per osservatori esterni e distanti un oggetto in caduta verso un buco nero, avvicinandosi al suo orizzonte degli eventi, appare rallentato fino a impiegare un tempo infinito per raggiungerlo.[36] Coerentemente l'osservatore esterno vedrebbe rallentato anche ogni altro processo fisico dell'oggetto in caduta. In sincronia con tale rallentamento la sua immagine sarebbe soggetta al fenomeno del red-shift gravitazionale,[37] sicché, al suo approssimarsi all'orizzonte, la luce che rendeva visibile l'oggetto si sposterebbe sempre più verso l'infrarosso[od oltre?] sino a diventare impercepibile. L'osservatore in caduta nel buco nero non noterebbe nessuno di suddetti cambiamenti mentre attraversa l'orizzonte degli eventi, in quanto il suo tempo proprio non varierebbe, e neppure sarebbe in grado di valutare esattamente il momento dell'attraversamento, essendo impossibile individuare con precisione i confini dell'orizzonte da parte di chi vi effettui misurazioni locali.[38] Egli noterebbe però nello spazio esterno al buco nero un comportamento diverso del tempo apparente, e cioè una velocizzazione estrema degli eventi; per identico motivo la luce indirizzata verso lui apparirebbe con lunghezza d'onda opposta a quella in allontanamento, manifestando il fenomeno del blue shift.[39]
La forma dell'orizzonte degli eventi di un buco nero è sempre approssimativamente sferica.[40][41][42] Per quelli non rotanti (o statici) la sua geometria è simmetrica (tutti i punti del suo confine distano ugualmente dal centro gravitazionale), mentre per buchi neri rotanti la forma è oblata (allargata lungo l'asse di rotazione) in misura più o meno pronunciata a secondo della velocità rotatoria: effetto calcolato da Larry Smarr (Stanford University) nel 1973.[43]
Singolarità
[modifica | modifica wikitesto]Al centro di un buco nero, come descritto dalla relatività generale, si trova una singolarità gravitazionale, una regione in cui la curvatura dello spaziotempo diventa infinita.[44] Per un buco nero non rotante, questa regione prende la forma di un unico punto, mentre per un buco nero rotante viene spalmata per formare una singolarità ad anello giacente nel piano di rotazione.[45] In entrambi i casi, la regione singolare ha volume pari a zero. Si può dimostrare che la regione singolare contiene tutta la massa del buco nero.[46] La regione singolare può quindi essere pensata come avente densità infinita.
Gli osservatori che cadono in un buco nero di Schwarzschild (cioè, non rotante e non carico) non possono evitare di essere trasportati nella singolarità una volta che attraversano l'orizzonte degli eventi. Gli osservatori possono prolungare l'esperienza accelerando verso l'esterno per rallentare la loro discesa, ma fino a un certo punto; dopo aver raggiunto una certa velocità ideale, è meglio la caduta libera per proseguire.[47] Quando raggiungono la singolarità, sono schiacciati a densità infinita e la loro massa è aggiunta alla massa totale del buco nero. Prima che ciò accada, essi sono comunque stati fatti a pezzi dalle crescenti forze di marea in un processo a volte indicato come spaghettificazione o "effetto pasta".[48] Nel caso di un buco nero rotante (Kerr) o carico (Reissner-Nordström), è possibile evitare la singolarità.
Estendendo queste soluzioni per quanto possibile, si rivela la probabilità, altamente ipotetico-speculativa, di un'uscita dal buco nero verso regioni spazio-temporali differenti e lontane (eventualmente anche altri universi[49]), col buco che funge da tunnel spaziale.[50] Comunque questa possibilità finora pare non più che teorica in quanto pur lievi perturbazioni basterebbero a distruggerne la via.[51] Sembrano inoltre non impossibili curve spaziotemporali chiuse di tipo tempo (che permetterebbero di ripercorrere il proprio passato) intorno alle singolarità di Kerr, però ciò implicherebbe problemi di causalità come il paradosso del nonno.[52]
Parte della comunità scientifica valuta che nessuno di questi effetti particolari possa verificarsi in un corretto trattamento quantico dei buchi neri rotanti e carichi.[53] La comparsa delle singolarità nella relatività generale è comunemente considerata elemento di rottura della teoria stessa.[54]
Tale inadeguatezza viene compensata dal ricorso alla fisica quantistica quando a descrivere detti processi si considerano gli effetti quantistici dovuti alla densità estremamente elevata della materia e pertanto alle interazioni tra particelle secondo la meccanica dei quanti. Non è stato ancora possibile combinare effetti quantistici e gravitazionali in una singola teoria, sebbene esistano tentativi di formulare una gravità quantistica. Si pensa che una tale teoria possa riuscire a escludere la presenza delle singolarità e dunque dei problemi fisici che esse pongono.[55][56]
Assenza di singolarità centrale secondo altre teorie
[modifica | modifica wikitesto]Il 10 dicembre 2018, Abhay Ashtekar, Javier Olmedo e Parampreet Singh hanno pubblicato un articolo scientifico nel campo della teoria della gravità ad anello che prevede l'assenza di singolarità centrale all'interno del buco nero, senza specificare geometricamente il futuro della materia a questo punto mentre il modello Janus propone una spiegazione[57][58][59]. Questo nuovo studio fornisce le stesse conclusioni di quelli ottenuti da lavori precedenti basati sulla relatività generale[60][61][62][63][64][65][66][67][68][69][70].
Sfera fotonica
[modifica | modifica wikitesto]La sfera fotonica è un confine sferico di spessore nullo tale che i fotoni che si spostano tangenti alla sfera sono intrappolati in un'orbita circolare. Per i buchi neri non-rotanti, la sfera fotonica ha un raggio di 1,5 volte il raggio di Schwarzschild. Le orbite sono dinamicamente instabili, quindi ogni piccola perturbazione (come una particella di materia in caduta) aumenterà nel tempo, tracciando o una traiettoria verso l'esterno che sfuggirà al buco nero o una spirale verso l'interno che eventualmente attraverserà l'orizzonte degli eventi.[71] Mentre la luce può ancora sfuggire dall'interno della sfera fotonica, ogni luce che l'attraversi con una traiettoria in entrata sarà catturata dal buco nero. Quindi qualsiasi luce che raggiunga un osservatore esterno dall'interno della sfera fotonica deve essere stata emessa da oggetti all'interno della sfera, ma ancora fuori dell'orizzonte degli eventi.[71] Altri oggetti compatti, come le stelle di neutroni, possono avere sfere fotoniche.[72] Ciò deriva dal fatto che il campo gravitazionale di un oggetto non dipende dalla sua dimensione effettiva, quindi ogni oggetto più piccolo di 1,5 volte il raggio di Schwarzschild corrispondente alla sua massa può effettivamente avere una sfera di fotoni.
Ergosfera
[modifica | modifica wikitesto]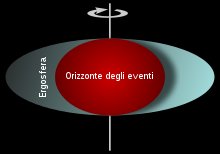
I buchi neri rotanti sono circondati da una regione dello spazio-tempo in cui è impossibile stare fermi chiamata ergosfera. Questo è il risultato di un processo noto come effetto di trascinamento; la relatività generale predice che qualsiasi massa rotante tenderà a "trascinare" leggermente tutto lo spazio-tempo immediatamente circostante. Qualsiasi oggetto vicino alla massa rotante tenderà a muoversi nella direzione della rotazione. Per un buco nero rotante questo effetto diventa così forte vicino all'orizzonte degli eventi che un oggetto, solo per fermarsi, dovrebbe spostarsi più veloce della velocità della luce nella direzione opposta.[73]
L'ergosfera di un buco nero è delimitata nella sua parte interna dal confine dell'orizzonte degli eventi (esterno) e da un sferoide schiacciato, che coincide con l'orizzonte degli eventi ai poli ed è notevolmente più largo intorno all'equatore. Il confine esterno è talvolta chiamato ergo-superficie. Gli oggetti e le radiazioni normalmente possono sfuggire dall'ergosfera. Attraverso il processo di Penrose, gli oggetti possono emergere dall'ergosfera con energia maggiore di quella d'entrata. Questa energia viene prelevata dalla energia di rotazione del buco nero, facendolo rallentare.
Formazione
[modifica | modifica wikitesto]
Considerando la natura esotica dei buchi neri, può essere naturale domandarsi se tali oggetti possano esistere in natura o asserire che siano soltanto soluzioni "patologiche" delle equazioni di Einstein. Einstein stesso pensò erroneamente che i buchi neri non si sarebbero formati perché ritenne che il momento angolare delle particelle collassate avrebbe stabilizzato il loro moto a un certo raggio.[74] Ciò condusse i relativisti del periodo a rigettare tutti i risultati contrari a questa teoria per molti anni. Tuttavia, una minoranza continuò a sostenere che i buchi neri fossero oggetti fisici[75] e, per la fine del 1960, la maggior parte dei ricercatori era convinta che non vi fosse alcun ostacolo alla formazione di un orizzonte degli eventi.
Penrose dimostrò che una volta formatosi un orizzonte degli eventi, si forma una singolarità da qualche parte all'interno di esso.[76] Poco dopo, Hawking dimostrò che molte soluzioni cosmologiche che descrivono il Big Bang hanno singolarità senza campi scalari o altra materia esotica (cfr. teoremi di singolarità di Penrose-Hawking). La soluzione di Kerr, il teorema no-hair e le leggi della termodinamica dei buchi neri hanno dimostrato che le proprietà fisiche dei buchi neri sono relativamente semplici, il che li rende "oggetti rispettabili per la ricerca".[77] Si pensa che il processo di formazione primaria per i buchi neri sia il collasso gravitazionale di oggetti pesanti come le stelle, ma ci sono anche processi più esotici che possono portare alla produzione di buchi neri.
Collasso gravitazionale
[modifica | modifica wikitesto]Verso il termine del proprio ciclo vitale, dopo aver consumato tramite fusione nucleare il 90% dell'idrogeno trasformandolo in elio, nel nucleo della stella si arrestano le reazioni nucleari. La forza gravitazionale, che prima era in equilibrio con la pressione generata dalle reazioni di fusione nucleare, prevale e comprime la massa della stella verso il suo centro.
Quando la densità diventa sufficientemente elevata può innescarsi la fusione nucleare dell'elio, in seguito alla quale c'è la produzione di litio, azoto e altri elementi (fino all'ossigeno e al silicio). Durante questa fase la stella si espande e si contrae violentemente più volte espellendo parte della propria massa. Le stelle più piccole si fermano a un certo punto della catena e si spengono, raffreddandosi e contraendosi lentamente, attraversano lo stadio di nana bianca e nel corso di molti milioni di anni diventano una sorta di gigantesco pianeta. In questo stadio la forza gravitazionale è bilanciata da un fenomeno quantistico, detto pressione di degenerazione, legato al principio di esclusione di Pauli. Per le nane bianche la pressione di degenerazione è presente tra gli elettroni.
Se invece il nucleo della stella supera una massa critica, detta limite di Chandrasekhar e pari a 1,44 volte la massa solare, le reazioni possono arrivare fino alla sintesi del ferro. La reazione che sintetizza il ferro per la formazione di elementi più pesanti è endotermica, richiede energia invece che emetterne, quindi il nucleo della stella diventa una massa inerte di ferro e non presentando più reazioni nucleari non c'è più nulla in grado di opporsi al collasso gravitazionale. A questo punto la stella subisce una contrazione fortissima che fa entrare in gioco la pressione di degenerazione tra i componenti dei nuclei atomici. La pressione di degenerazione arresta bruscamente il processo di contrazione, ma in questo caso può provocare una gigantesca esplosione, detta esplosione di supernova di tipo II.
Durante l'esplosione quel che resta della stella espelle gran parte della propria massa, che va a disperdersi nell'universo circostante. Quello che rimane è un nucleo estremamente denso e massiccio. Se la sua massa è abbastanza piccola da permettere alla pressione di degenerazione di contrastare la forza di gravità si arriva a una situazione di equilibrio e si forma una stella di neutroni.

Se la massa supera le tre masse solari (limite di Volkoff-Oppenheimer) non c'è più niente che possa contrastare la forza gravitazionale. Inoltre, secondo la relatività generale, la pressione interna non viene più esercitata verso l'esterno (in modo da contrastare il campo gravitazionale), ma diventa essa stessa una sorgente del campo gravitazionale rendendo così inevitabile il collasso infinito.
A questo punto la densità della stella morente, ormai diventata un buco nero, raggiunge velocemente valori tali da creare un campo gravitazionale talmente intenso da non permettere a nulla di sfuggire alla sua attrazione, neppure alla luce. È stato teorizzato che la curvatura infinita dello spaziotempo può far nascere un ponte di Einstein-Rosen o cunicolo spazio-temporale.
A causa delle loro caratteristiche i buchi neri non possono essere "visti" direttamente ma la loro presenza può essere ipotizzata a causa degli effetti di attrazione gravitazionale che esercitano nei confronti della materia vicina e della radiazione luminosa in transito nei paraggi o "in caduta" sul buco.
Esistono anche altri scenari che possono portare alla formazione di un buco nero. In particolare una stella di neutroni in un sistema binario può rubare massa alla sua vicina fino a superare la massa di Chandrasekhar e collassare. Alcuni indizi suggeriscono che questo meccanismo di formazione sia più frequente di quello "diretto".
Un altro scenario permette la formazione di buchi neri con massa inferiore alla massa di Chandrasekhar. Anche una quantità arbitrariamente piccola di materia, se compressa da una gigantesca forza esterna, potrebbe in teoria collassare e generare un orizzonte degli eventi molto piccolo. Le condizioni necessarie potrebbero essersi verificate nel primo periodo di vita dell'universo, quando la sua densità media era ancora molto alta a causa di variazioni di densità o di onde di pressione. Questa ipotesi è ancora completamente speculativa e non ci sono indizi che buchi neri di questo tipo esistano o siano esistiti in passato.
Buchi neri primordiali
[modifica | modifica wikitesto]Il collasso gravitazionale richiede una grande densità. Al momento nell'universo queste alte densità si trovano solo nelle stelle, ma nell'universo primordiale, poco dopo il Big Bang, le densità erano molto più elevate, e ciò probabilmente permise la creazione di buchi neri. Tuttavia la sola alta densità non è sufficiente a consentire la formazione di buchi neri poiché una distribuzione di massa uniforme non consente alla massa di convergere. Affinché si formino dei buchi neri primordiali, sono necessarie delle perturbazioni di densità che possano poi crescere grazie alla loro stessa gravità. Vi sono diversi modelli di universo primordiale che variano notevolmente nelle loro previsioni della dimensione di queste perturbazioni. Molti prevedono la creazione di buchi neri, che vanno da una massa di Planck a centinaia di migliaia di masse solari.[78] I buchi neri primordiali potrebbero così spiegare la creazione di qualsiasi tipo di buco nero.
Fenomenologia
[modifica | modifica wikitesto]La caratteristica fondamentale dei buchi neri è che il loro campo gravitazionale divide idealmente lo spaziotempo in due o più parti separate fra di loro da un orizzonte degli eventi. Un'informazione fisica (come un'onda elettromagnetica o una particella) potrà oltrepassare un orizzonte degli eventi in una direzione soltanto. Nel caso ideale, e più semplice, di un buco nero elettricamente scarico e non rotante (buco nero di Schwarzschild) esiste un solo orizzonte degli eventi che è una sfera centrata nell'astro e di raggio pari al raggio di Schwarzschild, che è funzione della massa del buco stesso. Una frase coniata dal fisico John Archibald Wheeler, un buco nero non ha capelli, sta a significare che tutte le informazioni sugli oggetti o segnali che cadono in un buco nero vengono perdute con l'eccezione di tre fattori: massa, carica e momento angolare. Il corrispondente teorema è stato dimostrato da Wheeler, che è anche colui che ha dato il nome a questi oggetti astronomici.
In realtà un buco nero potrebbe non essere del tutto nero: esso potrebbe emettere particelle, in quantità inversamente proporzionale alla sua massa, portando a una sorta di evaporazione. Questo fenomeno, proposto dal fisico Stephen Hawking nel 1974, è noto come radiazione di Hawking ed è alla base della termodinamica dei buchi neri. Alcune sue osservazioni sull'orizzonte degli eventi dei buchi neri, inoltre, hanno portato alla formulazione del principio olografico. Esiste una simulazione, effettuata al computer da alcuni ricercatori sulla base di osservazioni, che mostra l'incontro di una stella simile al Sole con un buco nero supermassiccio, dove la stella viene "triturata" e mentre alcuni detriti stellari "cadono" nel buco nero, altri vengono espulsi nello spazio a velocità elevata.[79][80] Un gruppo di astronomi analizzando i dati del Chandra X-ray Observatory della NASA ha invece scoperto l'espulsione di un buco nero ad altissima velocità dal centro di una galassia, dopo la fusione di due galassie.[81]
Altri effetti fisici sono associati all'orizzonte degli eventi, in particolare per la relatività generale il tempo proprio di un osservatore in caduta libera, agli occhi di un osservatore distante, appare più lento con l'aumentare del campo gravitazionale fino ad arrestarsi completamente sull'orizzonte. Quindi un astronauta che stesse precipitando verso un buco nero, se potesse sopravvivere all'enorme gradiente del campo gravitazionale, non percepirebbe nulla di strano all'avvicinarsi dell'orizzonte; al contrario un osservatore esterno vedrebbe i movimenti dello sfortunato astronauta rallentare progressivamente fino ad arrestarsi del tutto quando si trova a distanza uguale al raggio di Schwarzschild dal centro del buco nero.
Al contrario degli oggetti dotati di massa, i fotoni non vengono rallentati o accelerati dal campo gravitazionale del buco nero, ma subiscono un fortissimo spostamento verso il rosso (in uscita) o verso il blu (in entrata). Un fotone prodotto o posto esattamente sull'orizzonte degli eventi, diretto verso l'esterno del buco nero, subirebbe un tale spostamento verso il rosso da allungare all'infinito la sua lunghezza d'onda (la sua energia quindi diminuirebbe scendendo all'incirca a zero).
Uno dei primi oggetti nella Via Lattea candidati a essere un buco nero fu la sorgente di raggi X chiamata Cygnus X-1. Si ipotizza che enormi buchi neri (di massa pari a milioni di volte quella del Sole) esistano al centro delle galassie, la nostra e nella galassia di Andromeda. In questo caso si definiscono buchi neri supermassicci, la cui esistenza può essere verificata in modo indiretto misurando l'effetto sulla materia circostante del loro intenso campo gravitazionale. Nel nucleo centrale della nostra galassia, in particolare, si osserva l'esistenza di una forte sorgente radio ma molto compatta - nota come Sagittarius A* - la cui alta densità risulta compatibile solo con la struttura di un buco nero. Attualmente si calcola che le galassie osservabili abbiano di norma tale genere di buco nero nel loro nucleo: ciò permette anche di spiegare la forte emissione radiativa delle galassie attive (considerando la sequenza che comprende galassie come la nostra fino ai QSO). In pratica una trasformazione d'energia gravitazionale in energia elettromagnetica e cinetica attraverso la rotazione di ogni disco di accrescimento gassoso che tipicamente circonda i buchi neri.[82]
Modelli fisici e modelli matematici
[modifica | modifica wikitesto]
Un analogo fisico di un buco nero è il comportamento delle onde sonore in prossimità di un ugello de Laval: una strozzatura utilizzata negli scarichi dei razzi che fa passare il flusso dal regime subsonico a supersonico. Prima dell'ugello le onde sonore possono risalire il flusso del getto, mentre dopo averlo attraversato ciò è impossibile perché il flusso è supersonico, quindi più veloce del suono. Altri analoghi possono essere le onde superficiali in un liquido in moto in un canale circolare con altezza decrescente, un tubo per onde elettromagnetiche la cui velocità è alterata da un laser, una nube di gas di forma ellissoidale in espansione lungo l'asse maggiore.
Tutti questi modelli, se raffreddati fino alla condizione di condensato di Bose - Einstein, dovrebbero presentare l'analogo della radiazione di Hawking, e possono essere usati per correggere le previsioni di quest'ultima: come un fluido ideale, la teoria di Hawking considera la velocità della luce (suono) costante, indipendentemente dalla lunghezza d'onda (comportamento detto di Tipo I). Nei fluidi reali la velocità può aumentare (Tipo II) o diminuire (Tipo III) all'aumentare della lunghezza d'onda. Analogamente dovrebbe avvenire con la luce, ma se il risultato fosse che lo spazio tempo diffonde la luce come il Tipo II o il Tipo III, andrebbe modificata la relatività generale, cosa già nota perché per le onde con lunghezza d'onda prossima alla lunghezza di Planck diventa significativa la gravitazione quantistica.
Restando invece nel campo relativistico (ossia relativo alla teoria della relatività), poiché per descrivere un buco nero sono sufficienti tre parametri - massa, momento angolare e carica elettrica - i modelli matematici derivabili come soluzioni dell'equazione di campo della relatività generale si riconducono a quattro:
Buco nero di Schwarzschild
[modifica | modifica wikitesto]È la soluzione più semplice in quanto riguarda oggetti non rotanti e privi di carica elettrica, ma è anche piuttosto improbabile nella realtà, poiché un oggetto dotato anche di una minima rotazione una volta contratto in buco nero deve aumentare enormemente la sua velocità angolare in virtù del principio di conservazione del momento angolare.
Buco nero di Kerr
[modifica | modifica wikitesto]Deriva da oggetti rotanti e privi di carica elettrica, caso che presumibilmente corrisponde alla situazione reale. Buco nero risultante dal collasso di una stella in rotazione nel quale la singolarità non è più un punto, ma assume la forma di un anello a causa della rotazione. Per questa ragione si formeranno non uno ma due orizzonti degli eventi distinti. La rotazione del buco nero fa sì che si formi la cosiddetta ergosfera. Questa è la zona immediatamente circostante all'orizzonte esterno causata dall'intenso campo gravitazionale dove lo spaziotempo oltre a essere curvato entra in rotazione trascinato dalla rotazione del buco nero come un gigantesco vortice.
Buco nero di Kerr-Newman
[modifica | modifica wikitesto]Riguarda la situazione in cui si ha sia rotazione sia la carica elettrica ed è la soluzione più generale. In tale situazione lo spazio tempo non sarà asintoticamente piatto a causa della presenza del campo elettromagnetico.
Buco nero di Reissner-Nordström
[modifica | modifica wikitesto]È il caso di un buco nero dotato di carica elettrica ma non rotante. Valgono le stesse considerazioni fatte sul buco nero di Kerr-Newman a proposito del comportamento asintotico.
Primati
[modifica | modifica wikitesto]Per quanto riguarda i buchi neri supermassicci, TON 618 è un quasar distante 10,4 miliardi di anni luce dalla Terra che contiene un buco nero con massa pari a 66 miliardi di masse solari, il quale è, a oggi, il più grande buco nero mai scoperto.
Per quanto invece riguarda i buchi neri stellari, nel novembre del 2019 è stata annunciata su Nature la scoperta di un buco nero stellare di massa pari a 70 masse solari. Tale buco nero, ribattezzato LB-1 B (o LB-1 *) e distante circa 13 800 anni luce dalla Terra, fa parte di un sistema binario chiamato LB-1 ed è, a oggi, un enigma per gli astrofisici, poiché la sua massa è molto più grande di quanto fosse mai stato ipotizzato in base agli odierni modelli di evoluzione stellare.[83]
Ipotesi alternative
[modifica | modifica wikitesto]Stelle nere
[modifica | modifica wikitesto]Prima dello scatto della foto all’orizzonte degli eventi del buco nero M87, alcuni scienziati avevano messo in dubbio l'esistenza di tali oggetti come sono attualmente definiti e avevano ipotizzato che i corpi celesti identificati attualmente come buchi neri ma fino ad allora solo osservati indirettamente fossero in realtà "stelle nere" prive di orizzonte degli eventi. «Noi abbiamo dimostrato che certi effetti quantistici possono impedire ai buchi neri di formarsi, producendo invece un oggetto chiamato "stella nera", che non arriverebbe a densità infinita e non sarebbe avvolto dall'orizzonte degli eventi.»[84] Tali scienziati hanno visto come la definizione attuale di buco nero provochi alcuni paradossi: uno di questi è quello della perdita di informazioni. Questo paradosso consiste nel fatto che un buco nero, che contiene al suo interno un'enorme quantità di informazioni, evapori emettendo la radiazione di Hawking, che tuttavia non porta con sé nessuna informazione. Di conseguenza, durante l'evaporazione del buco nero, le informazioni contenute in esso svaniscono nel nulla. Questa perdita di informazioni contraddice una proprietà fondamentale della meccanica quantistica, l'unitarietà, secondo cui nessuna informazione può essere distrutta e costituisce il cosiddetto paradosso dell'informazione dei buchi neri.
Secondo la teoria delle stelle nere alcuni effetti quantistici (RSET) controbilancerebbero l'attrazione gravitazionale, impedendo così alla stella collassante di diventare un buco nero. Esse diventerebbero invece stelle nere che hanno alcune proprietà osservabili in comune con i buchi neri, ma anche molte differenze. Esse sarebbero infatti corpi materiali estremamente densi, fatti di materia densa e privi di orizzonte degli eventi. Sarebbero estremamente fioche a causa di un intenso spostamento verso il rosso della luce da loro emessa. Potrebbero emettere una radiazione analoga a quella di Hawking ma in questo caso non ci sarebbe perdita di informazioni (in quanto le radiazioni emesse dalle stelle nere, a differenza di quella di Hawking, trasporterebbero informazioni) e dunque il principio di unitarietà non verrebbe violato.
Poco prima della sua scomparsa, lo stesso Hawking pubblicò un articolo secondo cui le perturbazioni quantistiche in prossimità dell'orizzonte degli eventi permettono alla radiazione a lui intitolata di trasportare informazione (non essendo quindi prettamente termica) e grazie al principio di corrispondenza AdS/CFT l'informazione venga comunque conservata.[85]
Gravastar
[modifica | modifica wikitesto]Sono stelle di energia oscura di cui si è parlato ufficialmente per la prima volta nel 2005 al Lawrence Livermore National Laboratory in California. Il fisico George Chapline le ha presentate affermando che secondo la meccanica quantistica i buchi neri non sarebbero concepibili.
Fuzzball
[modifica | modifica wikitesto]Nel 2002 lo scienziato e astronomo Samir Mathur ha proposto una variante del modello dei buchi neri nel contesto della teoria delle stringhe. In questo modello si prevede che esista una regione di spazio in cui materia e radiazione possono risultare definitivamente intrappolati, come avviene per i buchi neri, ma il confine di tale regione (l'orizzonte degli eventi) non sarebbe una superficie in senso classico se visto a una scala microscopica. Per questo modello, quindi, è stato proposto il nome "fuzzball", ossia "palla pelosa".
Principio olografico
[modifica | modifica wikitesto]
Nel 1972 lo scienziato e astronomo Jacob Bekenstein si domandò cosa accade a un oggetto con entropia, ad esempio un gas caldo, quando varca l'orizzonte degli eventi: se essa scomparisse ciò comporterebbe una violazione del secondo principio della termodinamica, in quanto il contenuto aleatorio del gas scomparirebbe, una volta assorbito dal buco nero. La seconda legge può essere salvaguardata solo se si considerano i buchi neri come oggetti aleatori, con una enorme entropia, il cui incremento compensi abbondantemente l'entropia contenuta nel gas risucchiato. Il principio olografico trae origine dai calcoli effettuati sulla termodinamica dei buchi neri, che implicano che l'entropia massima possibile contenuta in una regione sia proporzionale alla superficie che racchiude la regione, non al suo volume, come ci si aspetterebbe (ovvero al quadrato del raggio, non al cubo).
Nel caso specifico del buco nero, la teoria comporta che il contenuto informativo caduto nel buco nero sia interamente contenuto nelle fluttuazioni superficiali dell'orizzonte degli eventi. Nel 1981 il fisico Stephen Hawking sollevò il paradosso informativo, dovuto all'entropia e conseguente evaporazione dei buchi neri, da lui stesso calcolata per altra via a partire dalle fluttuazioni quantistiche appena sopra l'orizzonte degli eventi, attraverso essa, sempre secondo Hawking, sarebbe scomparsa l'informazione intrappolata dall'orizzonte.
Nel 1993 il fisico Leonard Susskind propose una soluzione del paradosso basata sul principio della Complementarità (mutuato dalla fisica quantistica), per cui il gas in caduta entrerebbe "o" non entrerebbe dentro l'orizzonte, a seconda del punto di vista: da un punto di vista esterno un osservatore vedrebbe le stringhe, ovvero i componenti più elementari del gas, allargare le loro spire fino ad abbracciare la superficie dell'orizzonte degli eventi, dove si manterrebbe tutta l'informazione senza alcuna perdita per l'esterno, nemmeno in conseguenza della successiva evaporazione, mentre, per un osservatore che seguisse il gas in caduta, l'attraversamento dell'orizzonte avverrebbe, e avverrebbe senza particolari fenomeni di soglia, in conformità al principio relativistico (primo postulato della relatività ristretta), verso la singolarità. Il principio olografico risolverebbe dunque il paradosso informativo, nel contesto della teoria delle stringhe.
Altri oggetti affini ai buchi neri ipotizzati in via teorica
[modifica | modifica wikitesto]Sono state studiate a più riprese (a incominciare da Albert Einstein e Nathan Rosen negli anni trenta) altre soluzioni delle equazioni della relatività generale con singolarità dette buchi bianchi. Sono anche state ipotizzate, sempre a livello teorico, soluzioni ottenute per incollamento di due soluzioni con singolarità. Questi sono detti ponti di Einstein-Rosen o wormholes. Le possibili (controverse) interpretazioni fisiche di soluzioni di questo tipo hanno acceso la fantasia di numerosi scrittori di fantascienza.
Note
[modifica | modifica wikitesto]- ^ Da rilevare che non si tratta di una vera e propria fotografia ma del risultato dell'elaborazione di enormi quantità di dati non completi e troppo pesanti per essere spediti via Internet. Gli hard disk hanno viaggiato in aereo verso i due centri di calcolo dove si trovano i supercomputer altamente specializzati: all’Haystack Observatory del Mit, nel Massachusetts, e l’altro al Max Planck Institut fur Radioastronomie, a Bonn. (in Il Post.it, 10 aprile 2019)
- ^ Ecco la foto del secolo, è la prima di un buco nero, su ansa.it, ANSA, 10 aprile 2019. URL consultato il 10 aprile 2019.
- ^ Wald Robert M. (1984). General Relativity. University of Chicago Press, pp. 299. ISBN 978-0-226-87033-5.
- ^ “Volume interno di un Buco Nero” Archivio Pubblicazioni Università Cornell
- ^ Si veda il saggio di Kip Thorne del 1994 "Buchi neri e salti temporali" e nello specifico il capitolo III: "La scoperta e il rifiuto dei buchi neri".
- ^ C. Impey, I Mostri di Einstein, (Codice Edizioni, 2021)
- ^ (EN) J. Michell, On the means of discovering the distance, magnitude etc. of the fixed stars, in Philosophical Transactions of the Royal Society, 1784.
- ^ Introduction to the Theory of Black Holes., Institute for Theoretical Physics / Spinoza Institute. pp. 47–48.
- ^ Chandrasekhar and his limit., Universities Press. p. 89. ISBN 81-7371-035-X.
- ^ American Journal of Physics, 49 (5): 394–400. Bibcode:1981AmJPh..49..394D. doi:10.1119/1.12686.
- ^ Stellar evolution., A K Peters. p. 105. ISBN 1-56881-012-1.
- ^ Physical Review, 374–381. Bibcode:1939PhRv...55..374O. doi:10.1103/PhysRev.55.374
- ^ "Introducing the black hole"., Physics Today (1): 30–41.
- ^ A. Einstein, Annals of Mathematics, 2nd Ser., Vol. 40, No. 4. (Oct. 1939), p. 936
- ^ Oppenheimer, J. R. and Snyder, H. (1939). “On Continued Gravitational Contraction,” Physical Review. 56, 455.
- ^ A. Raychaudhuri, Phys. Rev. 89 (1953) p. 417
- ^ Scott A. Hughes, "Trust but verify: The case for astrophysical black holes
- ^ [Solitamente, gli astronomi italiani preferiscono usare la dizione inglese "No hair theorem"; la presente traduzione in italiano è stata proposta dal traduttore Emanuele Vinassa de Regny.
- ^ "Stationary Black Holes: Uniqueness and Beyond", Living Reviews in Relativity 1 (6). Archived from the original on 1999/02/03. Retrieved 2011-02-08.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, p. 253. ISBN 0-8053-8732-3., le note su cui si basa il libro sono disponibili gratuitamente nel sito Archiviato il 13 giugno 2007 in Internet Archive. di Sean Carroll
- ^ [Thorne, K. S.; Price, R. H. (1986). Black holes: the membrane paradigm. Yale University Press. ISBN 978-0-300-03770-8.
- ^ "The Black Hole Information Loss Problem" Archiviato il 22 gennaio 2009 in Internet Archive., Usenet Physics FAQ. Retrieved 2009-03-24.
- ^ "Black holes and information: A crisis in quantum physics", Caltech Theory Seminar.
- ^ [Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 7: 189–196. and Schwarzschild, K. (1916). "Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften 18: 424–434.
- ^ Hawking S. W.; Ellis G. F. R. (1973). Scale Structure of space time. Cambridge University Press, Appendice B. ISBN 0-521-09906-4.
- ^ Perspectives on Astronomy, Cengage Learning, p. 167, ISBN 0-495-11352-2
- ^ [Shapiro, S. L.; Teukolsky, S. A. (1983). Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley and Sons. p. 357. ISBN 0-471-87316-0.
- ^ Wald Robert M. (1997). "Gravitational Collapse and Cosmic Censorship". arXiv:gr-qc/9710068 [gr-qc].
- ^ "Numerical Approaches to Spacetime Singularities", Living Reviews in Relativity 5. Retrieved 2007-08-04.
- ^ [McClintock, J. E.; Shafee, R.; Narayan, R.; Remillard, R. A.; Davis, S. W.; Li, L.-X. (2006). "The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105". Astrophysical Journal 652 (1): 518–539. arXiv:astro-ph/0606076. Bibcode:2006ApJ...652..518M. doi:10.1086/508457.
- ^ Plutone e i Pianeti Nani: caratteristiche e orbita, in Oilproject. URL consultato il 27 maggio 2018.
- ^ Robert M. (1984). General Relativity. University of Chicago Press, pp. 124–125. ISBN 978-0-226-87033-5.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, Ch. 5.4 and 7.3. ISBN 0-8053-8732-3.,
- ^ [Wheeler, J. Craig (2007). Cosmic Catastrophes (2nd ed.). Cambridge University Press. ISBN 0-521-85714-7., p. 179.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, Ch. 5.4 and 7.3. ISBN 0-8053-8732-3.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, p.218. ISBN 0-8053-8732-3.,
- ^ "Inside a black hole", Knowing the universe and its secrets. Retrieved 2009-03-26.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, p.222. ISBN 0-8053-8732-3.
- ^ Vedi paragrafo "L'orizzonte degli eventi", capitolo XXXIII "Il buco nero", del saggio: "INFINITO. Viaggio ai limiti dell'universo" di Tullio Regge. Seconda edizione maggio 1995. Arnoldo Mondatori Editore S.p.A, Milano.
- ^ [Questo è vero solo per uno spazio-tempo a 4 dimensioni. In dimensioni superiori esistono topologie differenti dell'orizzonte, come gli anelli neri.
- ^ "Black Holes in Higher Dimensions" Archiviato il 27 marzo 2011 in Internet Archive., Living Reviews in Relativity 11 (6). arXiv:0801.3471. Bibcode:2008LRR....11....6E. Retrieved 2011-02-10.
- ^ [Obers, N. A. (2009). "Black Holes in Higher-Dimensional Gravity". In Papantonopoulos, Eleftherios. Lecture Notes in Physics 769: 211–258. arXiv:0802.0519. doi:10.1007/978-3-540-88460-6.
- ^ Kip. Thorne. Buchi neri e salti temporali. Cap.VII. pag.303. Edizioni Specchi (Castelvecchi) 2015..
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, p.205. ISBN 0-8053-8732-3.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, p.264-265. ISBN 0-8053-8732-3.,
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, p.252. ISBN 0-8053-8732-3.
- ^ [Lewis, G. F.; Kwan, J. (2007). "No Way Back: Maximizing Survival Time Below the Schwarzschild Event Horizon". Publications of the Astronomical Society of Australia 24 (2): 46–52. arXiv:0705.1029. Bibcode:2007PASA...24...46L. doi:10.1071/AS07012.
- ^ [Wheeler, J. Craig (2007). Cosmic Catastrophes (2nd ed.). Cambridge University Press., p. 182. ISBN 0-521-85714-7
- ^ Vedi diagrammi di Penrose per buco nero di Kerr estremo in William J.Kaufmann "Le Nuove Frontiere Dell'Astronomia" cap.11 "Buchi neri rotanti" pg.188 e "La geometria della soluzione di Kerr" pp. 204-207. Sansoni Editore 1980..
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, pp. 257–259 and 265–266. ISBN 0-8053-8732-3.,
- ^ "Black holes: the inside story", Physics World 9 (1): 34–37. Bibcode:1996PhyW....9...34D.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley., pag.266. ISBN 0-8053-8732-3.
- ^ [Poisson, E.; Israel, W. (1990). "Internal structure of black holes". Physical Review D 41 (6): 1796. Bibcode:1990PhRvD..41.1796P. doi:10.1103/PhysRevD.41.1796.
- ^ Wald Robert M. (1984). General Relativity. University of Chicago Press, pp. 212. ISBN 978-0-226-87033-5.
- ^ "Black Holes and Quantum Gravity", Cambridge Relativity and Cosmology. University of Cambridge. Retrieved 2009-03-26.
- ^ "Ask an Astrophysicist: Quantum Gravity and Black Holes", NASA. Retrieved 2009-03-26.
- ^ Abhay Ashtekar, Javier Olmedo e Parampreet Singh, Quantum Transfiguration of Kruskal Black Holes, in Physical Review Letters, vol. 121, n. 24, 10 dicembre 2018, p. 241301, Bibcode:2018PhRvL.121x1301A, DOI:10.1103/PhysRevLett.121.241301, ISSN 0031-9007, PMID 30608746, arXiv:1806.00648.
- ^ (EN) Carlo Rovelli, Viewpoint: Black Hole Evolution Traced Out with Loop Quantum Gravity, in Physics, vol. 11, 10 dicembre 2018.
- ^ (FR) Thomas Boisson, La gravité quantique à boucles fait disparaître la singularité centrale des trous noirs, su Trust My Science, 21 dicembre 2018. URL consultato il 22 dicembre 2018.
- ^ L. S. Abrams, Alternative space-time for the point mass, in Physical Review D, vol. 20, n. 10, 15 novembre 1979, pp. 2474-2479, Bibcode:1979PhRvD..20.2474A, DOI:10.1103/PhysRevD.20.2474, arXiv:gr-qc/0201044.
- ^ Abrams, L. S. (1989). "Black Holes: The Legacy of Hilbert's Error". Canadian Journal of Physics 67 (9): 919–926. doi:10.1139/p89-158. arXiv:gr-qc/0102055.
- ^ S. Antoci e D.-E. Liebscher, <137::AID-ASNA137>3.0.CO;2-1 Reconsidering Schwarzschild's original solution, in Astronomische Nachrichten, Issn2=1521-3994, vol. 322, n. 3, luglio 2001, pp. 137-142, Bibcode:2001AN....322..137A, DOI:10.1002/1521-3994(200107)322:3<137::AID-ASNA137>3.0.CO;2-1, ISSN 0004-6337, arXiv:gr-qc/0102084.
- ^ Salvatore Antoci, David Hilbert and the origin of the "Schwarzschild solution", in Meteorological and Geophysical Fluid Dynamics, 21 ottobre 2003, p. 343, Bibcode:2004mgfd.book..343A, arXiv:physics/0310104.
- ^ Pierre Fromholz, Eric Poisson e Clifford M. Will, The Schwarzschild metric: It's the coordinates, stupid!, in American Journal of Physics, Issn2=1943-2909, vol. 82, n. 4, aprile 2014, pp. 295-300, Bibcode:2014AmJPh..82..295F, DOI:10.1119/1.4850396, ISSN 0002-9505, arXiv:1308.0394.
- ^ Igor Mol, Revisiting the Schwarzschild and the Hilbert-Droste Solutions of Einstein Equation and the Maximal Extension of the Latter, su arxiv.org, 10 marzo 2014.
- ^ (EN) Jean-Pierre Petit, Black holes do not exist, in Researchgate, aprile 2014.
- ^ (FR) Les trous noirs n'existent pas - Partie 1, in La Voie de la Russie / Sputnik News, 30 giugno 2014. URL consultato il 12 gennaio 2019 (archiviato dall'url originale il 6 dicembre 2018).
- ^ (FR) Les trous noirs n'existent pas - Partie 2, in La Voie de la Russie - SputnikNews, 1º luglio 2014. URL consultato il 12 gennaio 2019 (archiviato dall'url originale il 6 dicembre 2018).
- ^ (EN) Jean-Pierre Petit, Schwarzschild 1916 seminal paper revisited : A virtual singularity, ResearchGate, 4 luglio 2016.
- ^ Jean-Pierre Petit e G. D'Agostini, Cancellation of the central singularity of the Schwarzschild solution with natural mass inversion process, in Modern Physics Letters A, vol. 30, n. 09, 27 febbraio 2015, p. 1550051, DOI:10.1142/S0217732315500510. URL consultato il 14 gennaio 2019.
- ^ a b [Nitta, Daisuke; Chiba, Takeshi; Sugiyama, Naoshi (September 2011), "Shadows of colliding black holes", Physical Review D 84 (6), arXiv:1106.242, Bibcode:2011PhRvD..84f3008N, doi:10.1103/PhysRevD.84.063008
- ^ [Nemiroff, R. J. (1993). "Visual distortions near a neutron star and black hole". American Journal of Physics 61 (7): 619. arXiv:astro-ph/9312003. Bibcode:1993AmJPh..61..619N. doi:10.1119/1.17224.
- ^ [Carroll, Sean M. (2004). Spacetime and Geometry. Addison Wesley, Ch. 6.6 ISBN 0-8053-8732-3.
- ^ [Einstein, A. (1939). "On A Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses". Annals of Mathematics 40 (4): 922–936. doi:10.2307/1968902.
- ^ [Kerr, R. P. (2009). "The Kerr and Kerr-Schild metrics". In Wiltshire, D. L.; Visser, M.; Scott, S. M. The Kerr Spacetime. Cambridge University Press. arXiv:0706.1109. ISBN 978-0-521-88512-6.
- ^ Penrose R.(1965). ["Gravitational Collapse and Space-Time Singularities". Physical Review Letters 14 (3): 57. Bibcode:1965PhRvL..14...57P. doi:10.1103/PhysRevLett.14.57.
- ^ Stephen Hawking e Roger Penrose (gennaio 1970). "The Singularities of Gravitational Collapse and Cosmology". Proceedings of the Royal Society A 314 (1519): 529–548. Bibcode:1970RSPSA.314..529H. doi:10.1098/rspa.1970.0021. JSTOR 2416467.
- ^ [Carr, B. J. (2005). "Primordial Black Holes: Do They Exist and Are They Useful?". In Suzuki, H.; Yokoyama, J.; Suto, Y. et al. Inflating Horizon of Particle Astrophysics and Cosmology. Universal Academy Press. arXiv:astro-ph/0511743. ISBN 4-946443-94-0.
- ^ NASA - Black Hole Caught Red-Handed in a Stellar Homicide
- ^ La stella dilaniata da un buco nero - Wired.it
- ^ Come cacciare un buco nero dalla propria galassia - Wired.it
- ^ Il percorso della ricerca condotta, allora ancora in divenire, per approdare a tali conclusioni è ben sintetizzato nel saggio astrofisico scritto e pubblicato nel 1992 e aggiornato nel 1999 da Margherita Hack "L'universo alle soglie del Duemila" cap.settimo pp.86-87 e cap.decimo pp.185-189. Superbur saggi-Biblioteca Universale Rizzoli 1999.
- ^ Quel buco nero non dovrebbe esistere, INAF, 27 novembre 2019. URL consultato il 28 novembre 2019.
- ^ Le scienze numero 496, Stelle nere non buchi neri, pag. 62
- ^ Phys. Rev. D 72, 084013 (2005): Information loss in black holes
Bibliografia
[modifica | modifica wikitesto]- A. Einstein, Zur allgemeinen Relativitatstheorie, Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften (1915) 778, Addendum-ibid. (1915) 799
- K. Schwarzschild, On the gravitational field of a sphere of incompressible fluid according to Einstein's theory, Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.) 1916 (1916) 424-434
- M.D. Kruskal, Maximal Extension of Schwarzschild Metric, Phys. Rev. 119, 1743 (1960)
- R. Kerr, Gravitational field of a spinning mass as an example of algebraically special metrics, Physical Review Letters 11 237-238 (1963).
- R.H. Boyer, R.W. Lindquist, Maximal analytic extension of the Kerr metric, J. Math. Phys. 8, 265-81 (1967)
- Jacob Bekenstein, Buchi neri, comunicazione, energia, Di Renzo Editore
- Stephen Hawking, Dal big bang ai buchi neri. Breve storia del tempo, Rizzoli, Milano, 2000
- Stephen Hawking, Dove il tempo si ferma. La nuova teoria sui buchi neri, Rizzoli, 2016
- Immanuel Kant, Metaphysiche Anfangsgründe der Naturwissenschaft, ediz. II, pag. 33
- John Taylor, I buchi neri. La fine dell'universo?, Eco, Milano, 2002
- Kip Thorne, Buchi neri e salti temporali. L'eredità di Einstein, Castelvecchi, 2017
- Mitchell Begelman, L'attrazione fatale della gravità. I buchi neri dell'universo, Zanichelli, Bologna, 1997
- H. Stephani, D. Kramer, M. MacCallum, C.Hoenselaers, and E. Herlt, Exact Solutions of Einstein's Field Equations, (Cambridge University Press, 2002).
Voci correlate
[modifica | modifica wikitesto]- Blanet
- Buco bianco
- Buco nero acustico
- Buco nero AdS
- Buco nero binario
- Buco nero di Kerr-Newman
- Buco nero di massa intermedia
- Buco nero di Planck
- Buco nero stellare
- Buco nero supermassiccio
- CERN
- Collapsar
- Coordinate di Gullstrand-Painlevé
- Disco di accrescimento
- Ergosfera
- Flusso oscuro
- Massa di Chandrasekhar
- Quasistar
- Radiazione di Hawking
- Raggio di Schwarzschild
- SDSS J0100+2802
- Teorema no-hair
Altri progetti
[modifica | modifica wikitesto] Wikiquote contiene citazioni di o su buco nero
Wikiquote contiene citazioni di o su buco nero Wikimedia Commons contiene immagini o altri file su buco nero
Wikimedia Commons contiene immagini o altri file su buco nero
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) black hole, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN, FR) Buco nero, su Enciclopedia canadese.
- (EN) Buco nero, su The Encyclopedia of Science Fiction.
- Chi ha paura dei buchi neri?, percorso in italiano - ScienzaPerTutti, su scienzapertutti.lnf.infn.it. URL consultato il 3 dicembre 2012 (archiviato dall'url originale il 13 dicembre 2014).
- Teoria dei buchi neri [collegamento interrotto], su ulisse.sissa.it.
- Buchi neri e loro effetti relativistici, su bo.astro.it.
- Storia dei buchi neri dalla loro scoperta a oggi, su torinoscienza.it (archiviato dall'url originale il 27 agosto 2007).
- Articolo di P.K.Townsend, richiede un ottimo livello (PDF), su arxiv.org.
- Hamed Moradi, "An Early History of Black Holes", (2004) Monash University
- Manuale dei buchi neri, su web.tiscali.it.
- Hawking Radiation Calculator Archiviato il 14 ottobre 2008 in Internet Archive. – Calcolatore online delle diverse proprietà di un buco nero immaginario a partire da un parametro noto
| Controllo di autorità | Thesaurus BNCF 17881 · LCCN (EN) sh85014574 · GND (DE) 4053793-6 · BNE (ES) XX528239 (data) · BNF (FR) cb11933630s (data) · J9U (EN, HE) 987007283120105171 · NDL (EN, JA) 00561056 |
|---|


 French
French Deutsch
Deutsch

