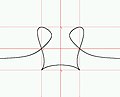
In matematica una curva quintica è una curva algebrica piana di quinto grado . Può essere definita da un polinomio della forma:
A x 5 + B y 5 + C x 4 y + D x y 4 + E x 3 y 2 + F x 2 y 3 + G x 4 + H y 4 + I x 3 y + J x y 3 + K x 2 y 2 + L x 3 + M y 3 + N x 2 y + O x y 2 + P x 2 + Q y 2 + R x y + S x + T y + U = 0 {\displaystyle Ax^{5}+By^{5}+Cx^{4}y+Dxy^{4}+Ex^{3}y^{2}+Fx^{2}y^{3}+Gx^{4}+Hy^{4}+Ix^{3}y+Jxy^{3}+Kx^{2}y^{2}+Lx^{3}+My^{3}+Nx^{2}y+Oxy^{2}+Px^{2}+Qy^{2}+Rxy+Sx+Ty+U=0} L'equazione ha 21 coefficienti, ma la curva non cambia se li moltiplichiamo tutti per una costante non nulla. Quindi i coefficienti essenziali sono 20 e le quintiche sono ∞ 20 {\displaystyle ^{20}}
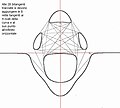
Curva a 28 bitangenti Una curva quintica (n=5) irriducibile può avere al massimo:
(n-1)(n-2)/2 + 1 = 7 componenti connesse (n-1)(n-2)/2 = 6 punti doppi n(n-2)(n-3)(n+3)/2 = 120 rette bitangenti 3n(n-2) = 45 punti di flesso. x 5 − y 2 − x = 0 {\displaystyle x^{5}-y^{2}-x=0}
x 5 + x 2 y − y 2 = 0 {\displaystyle x^{5}+x^{2}y-y^{2}=0}
y 2 ( y − 1 ) ( y − 2 ) ( y + 5 ) − ( x 2 − 1 ) 2 = 0 {\displaystyle y^{2}(y-1)(y-2)(y+5)-(x^{2}-1)^{2}=0}
25 x 5 + 45 y 5 + 68 x 4 − 155 y 4 − 12 x 3 + 175 y 3 − 35 x 2 − 65 y 2 + x + 4 = 0 {\displaystyle 25x^{5}+45y^{5}+68x^{4}-155y^{4}-12x^{3}+175y^{3}-35x^{2}-65y^{2}+x+4=0}
( x 2 + y 2 ) 2 ( y − 2 ) + y ( 4 x 4 + x 2 + y 2 ) = 0 {\displaystyle (x^{2}+y^{2})^{2}(y-2)+y(4x^{4}+x^{2}+y^{2})=0}
x 4 ( x − 1 ) + y 4 ( y − 1 ) − x y = 0 {\displaystyle x^{4}(x-1)+y^{4}(y-1)-xy=0}
x 5 + y 5 − x = 0 {\displaystyle x^{5}+y^{5}-x=0}
4 y 5 + 24 x 4 y + 35 x 2 y 3 − 21 x 4 − 45 x 2 y 2 − 40 y 3 − 46 x 2 y − 13 y 2 + 57 y + 36 = 0 {\displaystyle 4y^{5}+24x^{4}y+35x^{2}y^{3}-21x^{4}-45x^{2}y^{2}-40y^{3}-46x^{2}y-13y^{2}+57y+36=0}
36864 y 5 + 84375 x 4 − 24576 a 2 y 4 + 144000 a x 2 y 2 + 4096 a 4 y 3 − 86400 a 3 x 2 y + 13824 a 5 x 2 = 0 {\displaystyle 36864y^{5}+84375x^{4}-24576a^{2}y^{4}+144000ax^{2}y^{2}+4096a^{4}y^{3}-86400a^{3}x^{2}y+13824a^{5}x^{2}=0}
y 5 + 5 ( x 4 − y 4 − 1 ) = 0 {\displaystyle y^{5}+5(x^{4}-y^{4}-1)=0}
x 2 ( 13 y 3 − 5 x 2 + 33 y 2 + 36 y + 14 ) + y ( 2 x 4 + 5 y 4 + 15 y 3 + 12 y 2 − 10 y − 16 ) − 5 = 0 {\displaystyle x^{2}(13y^{3}-5x^{2}+33y^{2}+36y+14)+y(2x^{4}+5y^{4}+15y^{3}+12y^{2}-10y-16)-5=0}
x 2 ( 9 x 2 − 8 y 3 + 4 y 2 + 8 ) + y ( 9 x 4 + 3 y 4 − 7 y 3 + 4 y 2 + 5 y − 8 ) − 5 = 0 {\displaystyle x^{2}(9x^{2}-8y^{3}+4y^{2}+8)+y(9x^{4}+3y^{4}-7y^{3}+4y^{2}+5y-8)-5=0}
5 y 5 − x 4 − 2 y 3 + 2 x 2 − 1 = 0 {\displaystyle 5y^{5}-x^{4}-2y^{3}+2x^{2}-1=0}
y 5 + 100 x 4 y + 20 x 2 y 3 − 100 x + 10 y − 1000 = 0 {\displaystyle y^{5}+100x^{4}y+20x^{2}y^{3}-100x+10y-1000=0}
y 5 + 100 x 4 y + 20 x 2 y 3 + 100 x = 0 {\displaystyle y^{5}+100x^{4}y+20x^{2}y^{3}+100x=0}
x 5 + y 5 + x y ( x − y ) = 0 {\displaystyle x^{5}+y^{5}+xy(x-y)=0}
( x 2 − y 2 ) ( y 2 − 1 ) ( 2 y − 3 ) − y ( x 2 + y 2 − 2 y ) 2 = 0 {\displaystyle (x^{2}-y^{2})(y^{2}-1)(2y-3)-y(x^{2}+y^{2}-2y)^{2}=0}
x 2 ( x 2 − 2 ) + 2 y 2 ( y 3 + y 2 − 1 ) + 2 x 2 y ( x 2 − y 2 − 1 ) + 1 = 0 {\displaystyle x^{2}(x^{2}-2)+2y^{2}(y^{3}+y^{2}-1)+2x^{2}y(x^{2}-y^{2}-1)+1=0}
20 y ( x 2 + y 2 − 1 ) ( 5 x 2 + y 2 − 2 ) + 1 = 0 {\displaystyle 20y(x^{2}+y^{2}-1)(5x^{2}+y^{2}-2)+1=0}
x ( x y 3 − 14 x y + 1 ) + y ( y 4 + 10 x 4 − 6 y 2 + 4 ) = 0 {\displaystyle x(xy^{3}-14xy+1)+y(y^{4}+10x^{4}-6y^{2}+4)=0}
( 7 y 3 − 6 x 2 y − 8 x 2 + 7 y 2 + 4 ) ( 10 x 2 + 6 y 2 + 4 y − 9 ) − 1 = 0 {\displaystyle (7y^{3}-6x^{2}y-8x^{2}+7y^{2}+4)(10x^{2}+6y^{2}+4y-9)-1=0}
4 x 2 ( 3 x 3 + 2 x 2 − 13 x + 8 ) − 36 y 2 ( y 3 − 2 y 2 − 4 y + 8 ) + 3 x 2 y 2 ( 11 x − 10 y + 39 ) − 2 x y ( 2 x 3 − 18 y 3 + 29 x 2 + 57 y 2 + 59 x + 3 y − 90 ) = 0 {\displaystyle 4x^{2}(3x^{3}+2x^{2}-13x+8)-36y^{2}(y^{3}-2y^{2}-4y+8)+3x^{2}y^{2}(11x-10y+39)-2xy(2x^{3}-18y^{3}+29x^{2}+57y^{2}+59x+3y-90)=0}
Curva di Burnside
Curva Keratoide
Curva a staffa
Curva a Birilli
Curva di De L'Hospital
Curva di Mutasci
Curva sinuosa
Maracas di Chioppa
Butterfly Catastrophe
Curva a bulbo
Foglia di Patarino
Curva a tulipano
Curva a gocce
Curva con punto triplo
Impulso singolo
Doppio impulso
Curva bicuspinodata
Curva a 36 bitangenti
Curva con 10 flessi
Curva esaconnessa
Curva esanodata
French
Deutsch
Curva di Burnside
Curva Keratoide
Curva a staffa
Curva a Birilli
Curva di De L'Hospital
Curva di Mutasci
Curva sinuosa
Maracas di Chioppa
Butterfly Catastrophe
Curva a bulbo
Foglia di Patarino
Curva a tulipano
Curva a gocce
Curva con punto triplo
Impulso singolo
Doppio impulso
Curva bicuspinodata
Curva a 36 bitangenti
Curva con 10 flessi
Curva esaconnessa
Curva esanodata
Wikimedia Commons contiene immagini o altri file su Curva quintica
