Funzione W di Lambert
In matematica, la funzione W di Lambert, detta anche funzione Omega, è una funzione polidroma, costituita dai rami della funzione inversa della funzione definita dall'espressione f(w) = wew, dove ew è la funzione esponenziale nel campo complesso, mentre w è un qualsiasi numero complesso. In altre parole, l'equazione che definisce W(z) è
per qualsiasi numero complesso z.
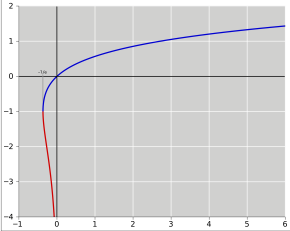
Poiché la funzione ƒ non è iniettiva, la funzione W, sua inversa, è una funzione polidroma (tranne che in 0). Restringendo l'attenzione al caso in cui W assuma solo valori reali, allora la relazione è definita solo per x ≥ −1/e, e vengono assunti due valori distinti nell'intervallo (−1/e, 0); la condizione aggiuntiva W ≥ −1 definisce una funzione univoca W0(x). Si ha W0(0) = 0 e W0(−1/e) = −1. Allo stesso tempo, il ramo inferiore ha W ≤ −1 e viene indicato con la notazione W−1(x). Esso decresce da W−1(−1/e) = −1 a W−1(0−) = −∞.
La funzione W non può essere espressa in termini di funzioni elementari. Essa trova applicazioni in combinatoria, ad esempio nell'enumerazione degli alberi. Può essere utilizzata nella risoluzione di equazioni che comprendono funzioni esponenziali (ad esempio i massimi delle distribuzioni di Planck, Bose-Einstein, e Fermi-Dirac) ed è inoltre necessaria nella risoluzione di equazioni differenziali del tipo y'(t) = a y(t − 1).
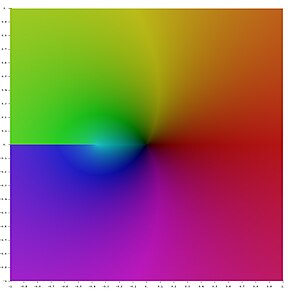
Ramo principale della funzione W nel piano complesso. La tonalità rappresenta l'argomento della funzione, mentre l'intensità rappresenta il modulo.
Storia e terminologia
[modifica | modifica wikitesto]La funzione W prende il nome dal matematico Johann Heinrich Lambert. Lambert studiò l'eponima Equazione trascendente di Lambert nel 1758, a cui seguì uno studio da parte di Eulero nel 1783, che considerò il caso speciale wew. Ad ogni modo, la funzione inversa di wew venne descritta per la prima volta da George Pólya e Gabor Szegő nel 1925. La funzione W di Lambert è stata "riscoperta" all'incirca ogni decennio in applicazioni specialistiche ma non se ne notò l'importanza fino alla fine degli anni '90.
Il ramo principale W0 è indicato con Wp nella Digital Library of Mathematical Functions mentre il ramo W−1 è ivi indicato con Wm. La notazione usata in questo articolo (con W0 e W−1) concorda con quella usata da Corless, Gonnet, Hare, Jeffrey e Knuth.
Analisi
[modifica | modifica wikitesto]Derivata
[modifica | modifica wikitesto]Tramite derivazione implicita, si può mostrare che tutti i rami di W soddisfano l'equazione differenziale
(W non è derivabile in z=−1/e). Ciò è conseguenza della seguente formula per la derivata di W:
Inoltre si ha
Infatti, essendo per definizione , si ha:
da cui:
In particolare, nel punto , la derivata della funzione vale 1, dunque la derivata della funzione , che ne è il reciproco, è prolungabile per continuità e vale 1.
Primitiva
[modifica | modifica wikitesto]La funzione W(x), e molte espressioni che incorporano W(x), possono essere integrate applicando la sostituzione w = W(x), cioè x = W eW:
Infatti:
con la sostituzione
integrando per parti
A questo punto, integrando per parti nell'ultimo termine:
e sostituendo nella precedente espressione, otteniamo:
Serie di Maclaurin
[modifica | modifica wikitesto]La serie di Maclaurin di può essere trovata usando il teorema di inversione di Lagrange ed è data da
Il raggio di convergenza è 1/e, come si può notare applicando il criterio della radice. La funzione definita da questa serie può essere estesa ad una funzione olomorfa definita per ogni numero complesso. Questa funzione definisce il ramo principale della funzione W di Lambert.
Interi e potenze complesse
[modifica | modifica wikitesto]Potenze intere di ammettono uno sviluppo in serie di Taylor (o di Laurent) centrata in 0
Più generalmente, per , la formula di inversione di Lagrange permette di ottenere
che è, generalmente, una serie di Laurent di ordine r. Equivalentemente, quest'ultima può essere scritta come serie di Taylor di
valida per ogni e .
Valori notevoli
[modifica | modifica wikitesto]Per ogni x algebrico non nullo W(x) è un numero trascendente. Questa proprietà può essere dimostrata per assurdo: se W(x) fosse algebrico e non nullo (si noti che se x è non nullo anche W(x) lo deve essere) allora per il teorema di Lindemann-Weierstrass eW(x) dovrebbe essere trascendente, implicando che anche x=W(x)eW(x) lo sia, contraddicendo l'ipotesi che x sia algebrico.
- dove indica la costante Omega
Altre proprietà integrali
[modifica | modifica wikitesto]Applicazioni
[modifica | modifica wikitesto]Molte equazioni che includono esponenziazioni possono essere risolte utilizzando la funzione W. La strategia generale è di spostare tutte le occorrenze dell'incognita ad un membro per ottenere una forma del tipo Y = XeX, punto in cui la funzione W fornisce il valore della variabile in X.
In altre parole:
Esempio 1
[modifica | modifica wikitesto]Più generalmente, l'equazione
dove
può essere trasformata tramite la sostituzione
in
ottenendo
che fornisce la soluzione finale
Similmente si deriva che l'equazione
ha per soluzione
Esempio 2
[modifica | modifica wikitesto]- con
Più in generale, per risolvere l'equazione:
dove
ci sono due modi.
Il primo consiste nell'elevare a ciascun membro di tale equazione, riconducendosi quindi all'esempio 1:
Il secondo è il seguente:
Esempio 3
[modifica | modifica wikitesto]- con
Esempio 4
[modifica | modifica wikitesto]L'equazione
può essere risolta con due tecniche differenti:
o, equivalentemente,
Si noti che le due forme sono equivalenti in quanto per la definizione stessa di W
Esempio 5
[modifica | modifica wikitesto]La tetrazione infinita
come dimostrato da Eulero nel 1783,[1] converge per e−e ≤ x ≤ e1/e ; come dimostrato poi da Eisenstein nel 1844,[2] la funzione W ne fornisce il valore limite:
Infatti, una volta stabilito l'intervallo di convergenza della tetrazione infinita, si può osservare che:
D'altra parte, questa espressione è equivalente a
Infatti, per definizione stessa di W:
da cui, posto , si ha:
Generalizzazioni
[modifica | modifica wikitesto]La funzione W di Lambert fornisce soluzioni reali per le equazioni algebrico-trascendenti (in x) della forma:
dove a0, c e r sono costanti reali. La soluzione è . Le generalizzazioni della funzione W di Lambert[3][4][5] includono:
- Un'applicazione alla relatività generale e alla meccanica quantistica (gravità quantistica) in bassa dimensione; si tratta di un collegamento precedentemente sconosciuto (prima dell'articolo del 2007 di Farrugia, Mann e Scott[6]) tra queste due aree:
- dove il membro destro di (1) è un polinomio quadratico in x, e r1 e r2 sono costanti reali distinte, le radici del polinomio quadratico. In questo caso, la soluzione è una funzione di un solo argomento x, e i termini ri e ao sono parametri di tale funzione. Da questo punto di vista, la generalizzazione ricorda la funzione ipergeometriche e la funzione G di Meijer ma appartiene ad una diversa classe di funzioni. Quando r1 = r2, entrambi i membri di (2) possono essere fattorizzati e ridotti al caso (1); la soluzione, quindi, è quella della funzione W standard. L'equazione (2) descrive il campo di dilatone, dal quale deriva la metrica del problema di gravità a due corpi R=T o lineale in 1+1 dimensioni (una dimensione spaziale e una dimensione temporale) per il caso di masse a riposo diverse, come anche le energie nel modello quantistico unidimensionale di una doppia buca di potenziale, con potenziali a delta di Dirac, per cariche diverse.
- Soluzioni analitiche delle energie di un caso particolare del problema quantistico dei tre corpi, più precisamente la molecola di idrogeno ionizzata una volta[7]. In questo caso il membro destro di (1) (o (2)) è un quoziente di polinomi in x di grado infinito:
- dove ri e si sono costanti reali distinti e x è una funzione dell'energia e della distanza internucleare R. L'equazione (3), con i casi particolari (1) e (2), ha un ruolo in un'ampia classe di equazioni differenziali con ritardo. Grazie alla nozione di un "falso derivato" di Hardy, radici multiple esatte sono state trovate per casi speciali di equazioni (3)[8].
Le applicazioni della funzione W di Lambert ai problemi di fisica fondamentale non sono esaurite neppure per il caso standard (1), come si è visto recentemente in fisica atomica, molecolare e ottica[9].
Valori numerici
[modifica | modifica wikitesto]La funzione W può essere approssimata utilizzando il metodo delle tangenti, con approssimazione successiva di (in modo che ) tramite
La funzione W può anche essere approssimata utilizzando il metodo di Halley,
Grafici
[modifica | modifica wikitesto]- Grafici della funzione W di Lambert nel piano complesso
- z = Re(W0(x + i y))
- z = Im(W0(x + i y))
- W0(x + i y)
Note
[modifica | modifica wikitesto]- ^ Euler, L. "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29–51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350–369, 1921. (facsimile)
- ^ La funzione W(x), su bitman.name. URL consultato il 20 luglio 2020.
- ^ T.C. Scott e R.B. Mann, General Relativity and Quantum Mechanics: Towards a Generalization of the Lambert W Function, AAECC (Applicable Algebra in Engineering, Communication and Computing), vol. 17, no. 1, (avril 2006), pp.41-47, [1]; articolo Arxiv [2]
- ^ T.C. Scott, G. Fee e J. Grotendorst, "Asymptotic series of Generalized Lambert W Function", SIGSAM, vol. 47, no. 3, (settembre 2013), pp. 75-83
- ^ T.C. Scott, G. Fee, J. Grotendorst e W.Z. Zhang, "Numerics of the Generalized Lambert W Function", SIGSAM, vol. 48, no. 2, (giugno 2014), pp. 42-56
- ^ P.S. Farrugia, R.B. Mann, e T.C. Scott, N-body Gravity and the Schrˆdinger Equation, Class. Quantum Grav. vol. 24, (2007), pp. 4647-4659, [3]; articolo Arxiv [4]
- ^ T.C. Scott, M. Aubert-Frécon e J. Grotendorst, New Approach for the Electronic Energies of the Hydrogen Molecular Ion, Chem. Phys. vol. 324, (2006), pp. 323-338, [5] Archiviato il 31 marzo 2009 in Internet Archive.; articolo Arxiv [6]
- ^ Aude Maignan e T.C. Scott, "Fleshing out the Generalized Lambert W Function", SIGSAM, vol. 50, no. 2, (giugno 2016), pp. 45-60
- ^ T.C. Scott, A. Lüchow, D. Bressanini e J.D. Morgan III, The Nodal Surfaces of Helium Atom Eigenfunctions, Phys. Rev. A 75, (2007), p. 060101, [7]
Voci correlate
[modifica | modifica wikitesto]Altri progetti
[modifica | modifica wikitesto] Wikimedia Commons contiene immagini o altri file su funzione W di Lambert
Wikimedia Commons contiene immagini o altri file su funzione W di Lambert
Collegamenti esterni
[modifica | modifica wikitesto]- (EN) Eric W. Weisstein, Funzione W di Lambert, su MathWorld, Wolfram Research.


 French
French Deutsch
Deutsch




































![{\displaystyle W\left({\frac {\sqrt[{n}]{e}}{n}}\right)={\frac {1}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a720a2a551ccfca9d58ff9355e73b3182036fbe0)






























































































