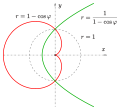
カージオイド(a=1 の場合)
カージオイド(a=1 の場合) カージオイド(英: cardioid)は、極座標の方程式

によって表される曲線である。心臓形(しんぞうけい)とも呼ばれる。心臓に似た形のためこの名称が付いた(ギリシア語: καρδιοειδής, kardioeides) =「καρδιά (kardia, 心臓)」 + 「είδος (eidos, 形)」)。
直交座標の方程式では

で、媒介変数表示では

で、それぞれ表される。
 円の垂足曲線として生成されるカージオイド。
円の垂足曲線として生成されるカージオイド。  カージオイドの尖点を通る弦。図中の変数 a(直線体)は、本文中の変数 a(斜体)の半分に相当することに注意。
カージオイドの尖点を通る弦。図中の変数 a(直線体)は、本文中の変数 a(斜体)の半分に相当することに注意。 - エピサイクロイドの一種と見なすことができる。またパスカルの蝸牛形(リマソン)の一種と見なすこともできる。
- 半径 a の円の、当該円周上の点を垂足点とする垂足曲線に相当する。
- x軸に対して線対称で、尖点は原点Oである。x軸とは原点Oと (2a, 0) で、y軸とは (0, ± a) で交わる。x軸から最も離れた点の座標は
 である。
である。 - 曲線で囲まれる面積 S と曲線の弧長 l は
 である。
である。
- 媒介変数 θ の地点における曲率半径は
 である。
である。 - 尖点を通る弦の長さは一定値 2a となる。当該任意の弦の中点は、尖点を通り直径 a の円周上に位置する。





 French
French Deutsch
Deutsch