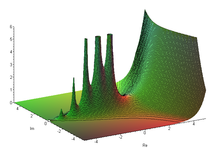
y = Γ(x )Γ(x + iy ) の絶対値x に相当、「Im」は y に相当)ガンマ関数 英 : gamma function )とは、数学において階乗 の概念を複素数 全体に拡張した特殊関数 。複素階乗とも。一般に Γ ( z ) {\displaystyle \Gamma (z)}
自然数 n {\displaystyle n} n {\displaystyle n}
n ! = Γ ( n + 1 ) , Γ ( n ) = ( n − 1 ) ! . {\displaystyle n!=\Gamma (n+1),\ \Gamma (n)=(n-1)!.} 1729年に数学者レオンハルト・オイラー によって無限乗積 の形で、最初に導入された[ 1] Γ {\displaystyle \Gamma } ルジャンドル が導入した[ 1] ガウス が得ており Π {\displaystyle \Pi } Π ( z ) = Γ ( z + 1 ) {\displaystyle \Pi (z)=\Gamma (z+1)}
実部 が正となる複素数 z {\displaystyle z} 広域積分 で定義される複素関数:
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t ( ℜ z > 0 , ) {\displaystyle \Gamma (z)=\int _{0}^{\infty }t^{z-1}e^{-t}\,{\rm {d}}t\qquad (\Re {z}>0,)} をガンマ関数 と呼ぶ[ 2] オイラー積分 とも呼ばれる。
一般の複素数 z {\displaystyle z} 解析接続 もしくは次の極限 で定義される。
Γ ( z ) = lim n → ∞ n z n ! ∏ k = 0 n ( z + k ) . {\displaystyle \Gamma (z)=\lim _{n\to \infty }{\frac {n^{z}n!}{\prod \limits _{k=0}^{n}{(z+k)}}}.} 他にも互いに同値となるいくつかの定義が存在する。
0 {\displaystyle 0} 負の整数 でない、かつ実部が正の任意の複素数 z {\displaystyle z}
Γ ( z + 1 ) = ∫ 0 ∞ e − t t z d t = [ − e − t t z ] 0 ∞ + z ∫ 0 ∞ e − t t z − 1 d t = z Γ ( z ) ( ∵ [ − e − t t z ] 0 ∞ = 0 ) , {\displaystyle {\begin{aligned}\Gamma (z+1)&=\int _{0}^{\infty }e^{-t}t^{z}\,{\rm {d}}t\\&={\Bigl [}-e^{-t}t^{z}{\Bigr ]}_{0}^{\infty }+z\int _{0}^{\infty }e^{-t}t^{z-1}\,{\rm {d}}t\\&=z\Gamma (z)\qquad \left(\because {\Bigl [}-e^{-t}t^{z}{\Bigr ]}_{0}^{\infty }=0\right)\!,\end{aligned}}} となることから、 Γ ( z + 1 ) = z Γ ( z ) {\displaystyle \Gamma (z+1)=z\Gamma (z)}
Γ ( 1 ) = ∫ 0 ∞ e − t d t = [ − e − t ] 0 ∞ = lim t → ∞ ( − e − t + 1 ) = 1 , {\displaystyle {\begin{aligned}\Gamma (1)&=\int _{0}^{\infty }e^{-t}\,{\rm {d}}t={\Bigl [}-e^{-t}{\Bigr ]}_{0}^{\infty }=\lim _{t\to \infty }\!\left(-e^{-t}+1\right)\\&=1,\end{aligned}}} である。これらの性質から、任意の正の整数 n {\displaystyle n}
Γ ( n + 1 ) = n Γ ( n ) = n ( n − 1 ) Γ ( n − 1 ) = ⋯ = n ! Γ ( 1 ) = n ! , {\displaystyle \Gamma (n+1)=n\Gamma (n)=n(n-1)\Gamma (n-1)=\cdots =n!\,\Gamma (1)=n!,} より Γ ( n + 1 ) = n ! {\displaystyle \Gamma (n+1)=n!} 階乗 の定義域を複素平面 に拡張したものとなっている。
歴史的には、ガンマ関数は「階乗の複素数への拡張となるもの」(複素階乗)の実例として、オイラー により考案された。階乗の複素数への拡張となる関数は無数に存在するが「正の実軸上で対数凸 である解析関数」という条件を付ければ、それは一意に定まりガンマ関数に他ならない(ボーア・モレルップの定理 )。
右半平面においてオイラー積分で定義されたガンマ関数は全平面に有理型 に解析接続 する。
ガンマ関数は零点 を持たず、原点と負の整数に一位の極を持つ。その留数 は、
Res ( Γ , − n ) = ( − 1 ) n n ! . {\displaystyle \operatorname {Res} (\Gamma ,\,-n)={\frac {(-1)^{n}}{n!}}.} である。
また、 1 / 2 {\displaystyle 1/2} ガウス積分 の結果に一致する。
Γ ( 1 2 ) = π . {\displaystyle \Gamma \!\left({\frac {1}{2}}\right)={\sqrt {\pi }}.} これより、自然数 n {\displaystyle n}
Γ ( 1 2 + n ) = ( 2 n − 1 ) ! ! 2 n π , {\displaystyle \Gamma \!\left({\frac {1}{2}}+n\right)={\frac {(2n-1)!!}{2^{n}}}{\sqrt {\pi }},} が成立することがわかる。ここで ! ! {\displaystyle !!} 二重階乗 を表す。この性質を利用して高次元の球の体積 と表面積を求めることができる。また、
Γ ( 1 2 − n ) = ( − 2 ) n ( 2 n − 1 ) ! ! π . {\displaystyle \Gamma \!\left({\frac {1}{2}}-n\right)={\frac {(-2)^{n}}{(2n-1)!!}}{\sqrt {\pi }}.} 定義の積分表示と極限表示が一致することを示す。
G n ( z ) = ∫ 0 n t z − 1 ( 1 − t n ) n d t {\displaystyle G_{n}(z)=\int _{0}^{n}{t^{z-1}\left(1-{\frac {t}{n}}\right)^{n}}{\rm {d}}t}
とすれば
lim n → ∞ ( 1 − t n ) n = e − t {\displaystyle \lim _{n\to \infty }{\left(1-{\dfrac {t}{n}}\right)^{n}}=e^{-t}} であるから直感的には
lim n → ∞ G n ( z ) = ∫ 0 ∞ t z − 1 e − t d t {\displaystyle \lim _{n\to \infty }{G_{n}(z)}=\int _{0}^{\infty }t^{z-1}e^{-t}{\rm {d}}t} である。(厳密にははさみうちの原理 によって証明される)t = nu
G n ( z ) = n z ∫ 0 1 u z − 1 ( 1 − u ) n d u {\displaystyle G_{n}(z)=n^{z}\int _{0}^{1}{u^{z-1}(1-u)^{n}}{\rm {d}}u}
となる.nz を除く部分を gn (z )
g 0 ( z ) = ∫ 0 1 u z − 1 d u = [ u z z ] u = 0 1 = 1 z {\displaystyle g_{0}(z)=\int _{0}^{1}{u^{z-1}}{\rm {d}}u=\left[{\frac {u^{z}}{z}}\right]_{u=0}^{1}={\frac {1}{z}}} g n ( z ) = ∫ 0 1 ( u z z ) ′ ( 1 − u ) n d u = n z ∫ u = 0 1 u z ( 1 − u ) n − 1 d u = n z g n − 1 ( z + 1 ) {\displaystyle g_{n}(z)=\int _{0}^{1}{\left({\frac {u^{z}}{z}}\right)'(1-u)^{n}}{\rm {d}}u={\frac {n}{z}}\int _{u=0}^{1}{u^{z}(1-u)^{n-1}}{\rm {d}}u={\frac {n}{z}}g_{n-1}(z+1)}
これにより
G n ( z ) = n z n ! ∏ k = 0 n ( z + k ) {\displaystyle G_{n}(z)={\frac {n^{z}n!}{\prod _{k=0}^{n}{(z+k)}}}}
を得る。故に
∫ 0 ∞ t z − 1 e − t d t = lim n → ∞ G n ( z ) = lim n → ∞ n z n ! ∏ k = 0 n ( z + k ) {\displaystyle \int _{0}^{\infty }t^{z-1}e^{-t}{\ d}t=\lim _{n\to \infty }G_{n}(z)=\lim _{n\to \infty }{\frac {n^{z}n!}{\prod _{k=0}^{n}{(z+k)}}}}
である。
オイラーの乗積表示からオイラーの定数
γ = lim n → ∞ ( ∑ k = 1 n 1 k − log n ) {\displaystyle \gamma =\lim _{n\to \infty }\left(\sum _{k=1}^{n}{\frac {1}{k}}-\log {n}\right)} を括り出すとワイエルシュトラスの乗積表示 が得られる。ワイエルシュトラス はガンマ関数が負の整数に極 を持つことを嫌って逆数を用いた[要出典 。ガンマ関数の逆数は複素平面全体で正則 である。
1 Γ ( z ) = lim n → ∞ ∏ k = 0 n ( z + k ) n z n ! = lim n → ∞ z n − z ( ∏ k = 1 n e z / k ) ( ∏ m = 1 n z + m m e − z / m ) = z e γ z ∏ m = 1 ∞ ( 1 + z m ) e − z / m {\displaystyle {\frac {1}{\Gamma (z)}}=\lim _{n\to \infty }{\frac {\prod _{k=0}^{n}{(z+k)}}{n^{z}n!}}=\lim _{n\to \infty }zn^{-z}\left(\prod _{k=1}^{n}{e^{z/k}}\right)\left(\prod _{m=1}^{n}{\frac {z+m}{m}}e^{-z/m}\right)=ze^{{\gamma }z}\prod _{m=1}^{\infty }\left(1+{\frac {z}{m}}\right)e^{-z/m}}
ガンマ関数は次の周回積分 で表される[ 5] − π ≤ arg ( − t ) ≤ π , 0 ≤ arg ( s ) ≤ 2 π {\displaystyle -\pi \leq \arg(-t)\leq \pi ,0\leq \arg(s)\leq 2\pi }
Γ ( z ) = i 2 sin π z ∫ C ( − t ) z − 1 e − t d t ( z ∈ C ∖ Z ) Γ ( z ) = 1 e 2 π i z − 1 ∫ C s z − 1 e − s d s ( z ∈ C ∖ Z ) 1 Γ ( z ) = i 2 π ∫ C ( − t ) − z e − t d t ( z ∈ C ) {\displaystyle {\begin{aligned}&\Gamma (z)={\frac {i}{2\sin {\pi }z}}\int _{C}(-t)^{z-1}e^{-t}{\rm {d}}t\qquad (z\in \mathbb {C} \setminus \mathbb {Z} )\\&\Gamma (z)={\frac {1}{e^{2{\pi }iz}-1}}\int _{C}s^{z-1}e^{-s}{\rm {d}}s\qquad (z\in \mathbb {C} \setminus \mathbb {Z} )\\&{\frac {1}{\Gamma (z)}}={\frac {i}{2\pi }}\int _{C}(-t)^{-z}e^{-t}{\rm {d}}t\qquad (z\in \mathbb {C} )\\\end{aligned}}}
これをハンケルの積分表示 と呼ぶ。このハンケルの積分表示は、積分経路を適当に変形し、数値積分でガンマ関数の値を求めるために使われることがある[ 6]
極座標表示 ( − t ) = r e i θ {\displaystyle (-t)=re^{i\theta }} θ = − π {\displaystyle \theta =-\pi } r = ∞ {\displaystyle r=\infty } r = δ {\displaystyle r=\delta } r = δ {\displaystyle r=\delta } θ = − π {\displaystyle \theta =-\pi } θ = π {\displaystyle \theta =\pi } θ = π {\displaystyle \theta =\pi } r = δ {\displaystyle r=\delta } r = ∞ {\displaystyle r=\infty }
∫ C ( − t ) z − 1 e − t d t = ∫ ∞ δ ( r e − π i ) z − 1 e − r d r + ∫ − π π ( δ e i θ ) z − 1 e δ e i θ ( − i δ e i θ ) d θ + ∫ δ ∞ ( r e π i ) z − 1 e − r d r = ∫ ∞ δ r z − 1 e − π i ( z − 1 ) e − r d r − ∫ − π π i δ z e i θ z e δ e i θ d θ + ∫ δ ∞ r z − 1 e π i ( z − 1 ) e − r d r = ( − e − π i ( z − 1 ) + e π i ( z − 1 ) ) ∫ δ ∞ r z − 1 e − r d r − ∫ − π π i δ z e i θ z e δ e i θ d θ = − 2 i sin π z ∫ δ ∞ r z − 1 e − r d r − ∫ − π π i δ z e i θ z e δ e i θ d θ {\displaystyle {\begin{aligned}\int _{C}(-t)^{z-1}e^{-t}{\rm {d}}t&=\int _{\infty }^{\delta }(re^{-{\pi }i})^{z-1}e^{-r}{\rm {d}}r+\int _{-\pi }^{\pi }({\delta }e^{i\theta })^{z-1}e^{{\delta }e^{i\theta }}(-i{\delta }e^{i\theta }){\rm {d}}\theta +\int _{\delta }^{\infty }(re^{{\pi }i})^{z-1}e^{-r}{\rm {d}}r\\&=\int _{\infty }^{\delta }r^{z-1}e^{-{\pi }i(z-1)}e^{-r}{\rm {d}}r-\int _{-\pi }^{\pi }i\delta ^{z}e^{i{\theta }z}e^{{\delta }e^{i\theta }}{\rm {d}}\theta +\int _{\delta }^{\infty }r^{z-1}e^{{\pi }i(z-1)}e^{-r}{\rm {d}}r\\&=\left(-e^{-{\pi }i(z-1)}+e^{{\pi }i(z-1)}\right)\int _{\delta }^{\infty }r^{z-1}e^{-r}{\rm {d}}r-\int _{-\pi }^{\pi }i\delta ^{z}e^{i{\theta }z}e^{{\delta }e^{i\theta }}{\rm {d}}\theta \\&=-2i\sin {\pi }z\int _{\delta }^{\infty }r^{z-1}e^{-r}{\rm {d}}r-\int _{-\pi }^{\pi }i\delta ^{z}e^{i{\theta }z}e^{{\delta }e^{i\theta }}{\rm {d}}\theta \\\end{aligned}}}
ℜ z > 0 {\displaystyle \Re {z}>0} δ → 0 {\displaystyle \delta \to 0} δ z → 0 {\displaystyle \delta ^{z}\to 0}
∫ C ( − t ) z − 1 e − t d t = − 2 i sin π z ∫ 0 ∞ r z − 1 e − r d r = − 2 i sin π z Γ ( z ) ( ℜ z > 0 ) {\displaystyle {\begin{aligned}\int _{C}(-t)^{z-1}e^{-t}{\rm {d}}t&=-2i\sin {\pi }z\int _{0}^{\infty }r^{z-1}e^{-r}{\rm {d}}r\\&=-2i\sin {\pi }z\Gamma (z)\qquad (\Re {z}>0)\\\end{aligned}}}
である。しかし、左辺の被積分関数は z {\displaystyle z}
Γ ( z ) = i 2 sin π z ∫ C ( − t ) z − 1 e − t d t ( z ∈ C ∖ Z ) {\displaystyle \Gamma (z)={\frac {i}{2\sin {\pi }z}}\int _{C}(-t)^{z-1}e^{-t}{\rm {d}}t\qquad (z\in \mathbb {C} \setminus \mathbb {Z} )}
である。 s = r e i θ {\displaystyle s=re^{i\theta }}
Γ ( z ) = 1 e 2 π i z − 1 ∫ C s z − 1 e − t d s ( z ∈ C ∖ Z ) {\displaystyle \Gamma (z)={\frac {1}{e^{2{\pi }iz}-1}}\int _{C}s^{z-1}e^{-t}{\rm {d}}s\qquad (z\in \mathbb {C} \setminus \mathbb {Z} )}
を得る。また、相反公式 により、
1 Γ ( z ) = sin π z π Γ ( 1 − z ) = i 2 π ∫ C ( − t ) − z e − t d t ( z ∈ C ) {\displaystyle {\frac {1}{\Gamma (z)}}={\frac {\sin {\pi }z}{\pi }}\Gamma (1-z)={\frac {i}{2\pi }}\int _{C}(-t)^{-z}e^{-t}{\rm {d}}t\qquad (z\in \mathbb {C} )}
を得る。
z → ∞ {\displaystyle z\to \infty } スターリングの公式 で近似される。この漸近近似は複素平面全体(負の実数を除く)で成立するが、 | arg z | = π {\displaystyle |{\arg z}|={\pi }} 相反公式 などを用いて | arg z | ≤ π / 2 {\displaystyle |{\arg z}|\leq {\pi }/2}
Γ ( z + 1 ) ≈ 2 π z ( z e ) z ( | arg z | < π , | z | ≫ 0 ) {\displaystyle \Gamma (z+1)\approx {\sqrt {2{\pi }z}}\left({\frac {z}{e}}\right)^{z}\qquad (|{\arg z}|<{\pi },|z|\gg 0)} lim z → ∞ Γ ( z + 1 ) 2 π z ( z e ) z = 1 ( | arg z | < π ) {\displaystyle \lim _{z\to \infty }{\frac {\Gamma (z+1)}{{\sqrt {2{\pi }z}}\left({\frac {z}{e}}\right)^{z}}}=1\qquad (|{\arg z}|<{\pi })}
次の恒等式 を相反公式 (reflection formula)という[ 7]
Γ ( z ) Γ ( 1 − z ) = − z Γ ( z ) Γ ( − z ) = π sin π z , z ∉ Z {\displaystyle \Gamma (z)\Gamma (1-z)=-z\Gamma (z)\Gamma (-z)={\frac {\pi }{\sin {{\pi }z}}},\qquad z\not \in \mathbb {Z} }
相補公式 とも呼ばれる。 この恒等式はオイラーの乗積表示から得られる。
− z Γ ( z ) Γ ( − z ) = − z ( lim n → ∞ n z n ! ∏ k = 0 n ( z + k ) ) ( lim n → ∞ n − z n ! ∏ k = 0 n ( − z + k ) ) = 1 z ∏ k = 1 ∞ k 2 k 2 − z 2 = π π z ∏ k = 1 ∞ k 2 − z 2 k 2 {\displaystyle {\begin{aligned}-z\Gamma (z)\Gamma (-z)&=-z\left(\lim _{n\to \infty }{\frac {n^{z}n!}{\prod _{k=0}^{n}{(z+k)}}}\right)\left(\lim _{n\to \infty }{\frac {n^{-z}n!}{\prod _{k=0}^{n}{(-z+k)}}}\right)\\&={\frac {1}{z}}\prod _{k=1}^{\infty }{\frac {k^{2}}{k^{2}-z^{2}}}\\&={\frac {\pi }{{\pi }z\displaystyle \prod _{k=1}^{\infty }\displaystyle {\frac {k^{2}-z^{2}}{k^{2}}}}}\\\end{aligned}}}
この分母は正弦関数の無限乗積展開 であるから、
Γ ( z ) Γ ( 1 − z ) = − z Γ ( z ) Γ ( − z ) = π sin π z {\displaystyle \Gamma (z)\Gamma (1-z)=-z\Gamma (z)\Gamma (-z)={\frac {\pi }{\sin {{\pi }z}}}}
である。相反公式に z = 1 2 {\displaystyle z={\frac {1}{2}}}
Γ ( 1 2 ) Γ ( 1 − 1 2 ) = π sin π 2 = π {\displaystyle \Gamma \left({\frac {1}{2}}\right)\Gamma \left(1-{\frac {1}{2}}\right)={\frac {\pi }{\sin {\frac {\pi }{2}}}}=\pi }
となり
Γ ( 1 2 ) = π {\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}
を得る。
次の恒等式をルジャンドルの倍数公式 と呼ぶ。これはガウスの乗法公式 の特別な場合である。
Γ ( z ) Γ ( z + 1 2 ) = 2 1 − 2 z π Γ ( 2 z ) {\displaystyle \Gamma (z)\Gamma \left(z+{\tfrac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z)}
ベータ関数 は以下のように表される。
B ( z 1 , z 2 ) = Γ ( z 1 ) Γ ( z 2 ) Γ ( z 1 + z 2 ) = ∫ 0 1 t z 1 − 1 ( 1 − t ) z 2 − 1 d t {\displaystyle \mathrm {B} (z_{1},z_{2})={\frac {\Gamma (z_{1})\Gamma (z_{2})}{\Gamma (z_{1}+z_{2})}}=\int _{0}^{1}t^{z_{1}-1}(1-t)^{z_{2}-1}\,dt} ここで z 1 = z 2 = z {\displaystyle z_{1}=z_{2}=z}
Γ 2 ( z ) Γ ( 2 z ) = ∫ 0 1 t z − 1 ( 1 − t ) z − 1 d t {\displaystyle {\frac {\Gamma ^{2}(z)}{\Gamma (2z)}}=\int _{0}^{1}t^{z-1}(1-t)^{z-1}\,dt} t = 1 + x 2 {\displaystyle t={\frac {1+x}{2}}}
Γ 2 ( z ) Γ ( 2 z ) = 1 2 2 z − 1 ∫ − 1 1 ( 1 − x 2 ) z − 1 d x {\displaystyle {\frac {\Gamma ^{2}(z)}{\Gamma (2z)}}={\frac {1}{2^{2z-1}}}\int _{-1}^{1}\left(1-x^{2}\right)^{z-1}\,dx} ( 1 − x 2 ) z − 1 {\displaystyle (1-x^{2})^{z-1}}
2 2 z − 1 Γ 2 ( z ) = 2 Γ ( 2 z ) ∫ 0 1 ( 1 − x 2 ) z − 1 d x {\displaystyle 2^{2z-1}\Gamma ^{2}(z)=2\Gamma (2z)\int _{0}^{1}(1-x^{2})^{z-1}\,dx} ここで
B ( 1 2 , z ) = ∫ 0 1 t 1 2 − 1 ( 1 − t ) z − 1 d t , t = s 2 {\displaystyle \mathrm {B} \left({\frac {1}{2}},z\right)=\int _{0}^{1}t^{{\frac {1}{2}}-1}(1-t)^{z-1}\,dt,\quad t=s^{2}} とすると
B ( 1 2 , z ) = 2 ∫ 0 1 ( 1 − s 2 ) z − 1 d s = 2 ∫ 0 1 ( 1 − x 2 ) z − 1 d x {\displaystyle \mathrm {B} \left({\frac {1}{2}},z\right)=2\int _{0}^{1}(1-s^{2})^{z-1}\,ds=2\int _{0}^{1}(1-x^{2})^{z-1}\,dx} よって
2 2 z − 1 Γ 2 ( z ) = Γ ( 2 z ) B ( 1 2 , z ) {\displaystyle 2^{2z-1}\Gamma ^{2}(z)=\Gamma (2z)\mathrm {B} \left({\frac {1}{2}},z\right)} よって
B ( 1 2 , z ) = Γ ( 1 2 ) Γ ( z ) Γ ( z + 1 2 ) , Γ ( 1 2 ) = π {\displaystyle \mathrm {B} \left({\frac {1}{2}},z\right)={\frac {\Gamma \left({\frac {1}{2}}\right)\Gamma (z)}{\Gamma \left(z+{\frac {1}{2}}\right)}},\quad \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}} よって以下の式が成り立つ。
Γ ( z ) Γ ( z + 1 2 ) = 2 1 − 2 z π Γ ( 2 z ) . {\displaystyle \Gamma (z)\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}{\sqrt {\pi }}\;\Gamma (2z).} 次の恒等式をガウスの乗法公式 (multiplication formula)という。
Γ ( n z ) = n n z − 1 / 2 ( 2 π ) ( n − 1 ) / 2 ∏ k = 0 n − 1 Γ ( z + k n ) {\displaystyle \Gamma (nz)={\frac {n^{nz-1/2}}{(2\pi )^{(n-1)/2}}}\prod _{k=0}^{n-1}{\Gamma {\left(z+{\frac {k}{n}}\right)}}}
両辺の比を f ( z ) {\displaystyle f(z)}
f ( z ) = n n z − 1 / 2 ∏ k = 0 n − 1 Γ ( z + k n ) ( 2 π ) ( n − 1 ) / 2 Γ ( n z ) {\displaystyle {\begin{aligned}f(z)=&{\frac {n^{nz-1/2}\prod _{k=0}^{n-1}{\Gamma {\left(z+{\frac {k}{n}}\right)}}}{(2\pi )^{(n-1)/2}\Gamma (nz)}}\\\end{aligned}}} f ( z + 1 ) = n n z − 1 / 2 n n [ ∏ k = 0 n − 1 ( z + k n ) Γ ( z + k n ) ] ( 2 π ) ( n − 1 ) / 2 [ ∏ k = 0 n − 1 ( n z + k ) ] Γ ( n z ) = n n z − 1 / 2 [ ∏ k = 0 n − 1 ( n z + k ) ] ∏ k = 0 n − 1 Γ ( z + k n ) ( 2 π ) ( n − 1 ) / 2 [ ∏ k = 0 n − 1 ( n z + k ) ] Γ ( n z ) = f ( z ) {\displaystyle {\begin{aligned}f(z+1)&={\frac {n^{nz-1/2}n^{n}\left[\prod _{k=0}^{n-1}\left(z+{\frac {k}{n}}\right)\Gamma {\left(z+{\frac {k}{n}}\right)}\right]}{(2\pi )^{(n-1)/2}\left[\prod _{k=0}^{n-1}(nz+k)\right]\Gamma (nz)}}\\&={\frac {n^{nz-1/2}\left[\prod _{k=0}^{n-1}\left(nz+k\right)\right]\prod _{k=0}^{n-1}\Gamma {\left(z+{\frac {k}{n}}\right)}}{(2\pi )^{(n-1)/2}\left[\prod _{k=0}^{n-1}(nz+k)\right]\Gamma (nz)}}\\&=f(z)\\\end{aligned}}}
故に、任意に大きな自然数 m {\displaystyle m} f ( z + m ) = f ( z ) {\displaystyle f(z+m)=f(z)}
lim ℜ z → + ∞ f ( z ) = lim ℜ z → + ∞ n n z − 1 / 2 [ ∏ k = 0 n − 1 2 π z + k / n ( z + k / n e ) z + k / n ] ( 2 π ) ( n − 1 ) / 2 2 π n z ( n z e ) n z = lim ℜ z → + ∞ z 1 / 2 [ ∏ k = 0 n − 1 z k / n − 1 / 2 ( 1 + k / n z ) z + k / n − 1 / 2 e − k / n ] = lim ℜ z → + ∞ z 1 / 2 [ ∏ k = 0 n − 1 z k / n − 1 / 2 e k / n e − k / n ] = 1 {\displaystyle {\begin{aligned}\lim _{\Re {z}\to +\infty }f(z)&=\lim _{\Re {z}\to +\infty }{\frac {n^{nz-1/2}\left[\prod _{k=0}^{n-1}{{\sqrt {\frac {2{\pi }}{z+k/n}}}\left({\frac {z+k/n}{e}}\right)^{z+k/n}}\right]}{(2\pi )^{(n-1)/2}{\sqrt {\frac {2{\pi }}{nz}}}\left({\frac {nz}{e}}\right)^{nz}}}\\&=\lim _{\Re {z}\to +\infty }z^{1/2}\left[\prod _{k=0}^{n-1}z^{k/n-1/2}(1+k/nz)^{z+k/n-1/2}e^{-k/n}\right]\\&=\lim _{\Re {z}\to +\infty }z^{1/2}\left[\prod _{k=0}^{n-1}z^{k/n-1/2}e^{k/n}e^{-k/n}\right]\\&=1\end{aligned}}}
途中で
lim ℜ z → + ∞ ( 1 + k / n z ) z + k / n − 1 / 2 = lim ℜ z → + ∞ ( 1 + k / n z ) z = e n / k {\displaystyle \lim _{\Re {z}\to +\infty }(1+k/nz)^{z+k/n-1/2}=\lim _{\Re {z}\to +\infty }(1+k/nz)^{z}=e^{n/k}}
を適用した。
f ( z ) = lim n → ∞ f ( z + n ) = 1 {\displaystyle f(z)=\lim _{n\to \infty }f(z+n)=1}
であり、故に
Γ ( n z ) = n n z − 1 / 2 ( 2 π ) ( n − 1 ) / 2 ∏ k = 0 n − 1 Γ ( z + k n ) {\displaystyle \Gamma (nz)={\frac {n^{nz-1/2}}{(2\pi )^{(n-1)/2}}}\prod _{k=0}^{n-1}{\Gamma {\left(z+{\frac {k}{n}}\right)}}}
が成立する。
( x , y , y 1 , … , y n ) {\displaystyle (x,\ y,\ y_{1},\ \ldots ,\ y_{n})} F ( x , y , y 1 , … , y n ) {\displaystyle F(x,\ y,\ y_{1},\ \ldots ,\ y_{n})}
F ( x , y , y 1 , ⋯ , y n ) = 0 , y i = d i y d x i ( i = 1 , ⋯ , n ) {\displaystyle F(x,y,y_{1},\cdots ,y_{n})=0,\quad y_{i}={\frac {d^{i}y}{dx^{i}}}\quad (i=1,\cdots ,n)}
の形で表される微分方程式を代数的微分方程式という。ガンマ関数はいかなる代数的微分方程式も満たさないことが知られている[ 7] ヘルダー が1887年に最初に証明を与えた後 [ 9] E. H. ムーア [ 10] A. オストロフスキ (英語版 ) [ 11] [ 12] E. バーンズ (英語版 ) [ 13] ハウスドルフ [ 14]
Γ ( − 3 2 ) = 4 π 3 ≈ 2.363 {\displaystyle \Gamma \left(-{\frac {3}{2}}\right)\,={\frac {4{\sqrt {\pi }}}{3}}\approx 2.363\,} Γ ( − 1 2 ) = − 2 π ≈ − 3.545 {\displaystyle \Gamma \left(-{\frac {1}{2}}\right)\,=-2{\sqrt {\pi }}\approx -3.545\,} Γ ( 1 2 ) = π ≈ 1.772 {\displaystyle \Gamma \left({\frac {1}{2}}\right)\,={\sqrt {\pi }}\approx 1.772\,} Γ ( 1 ) = 0 ! = 1 {\displaystyle \Gamma (1)\,=0!=1\,} Γ ( 3 2 ) = π 2 ≈ 0.886 {\displaystyle \Gamma \left({\frac {3}{2}}\right)\,={\frac {\sqrt {\pi }}{2}}\approx 0.886\,} Γ ( 2 ) = 1 ! = 1 {\displaystyle \Gamma (2)\,=1!=1\,} Γ ( 5 2 ) = 3 π 4 ≈ 1.329 {\displaystyle \Gamma \left({\frac {5}{2}}\right)\,={\frac {3{\sqrt {\pi }}}{4}}\approx 1.329\,} Γ ( 3 ) = 2 ! = 2 {\displaystyle \Gamma (3)\,=2!=2\,} Γ ( 7 2 ) = 15 π 8 ≈ 3.323 {\displaystyle \Gamma \left({\frac {7}{2}}\right)\,={\frac {15{\sqrt {\pi }}}{8}}\approx 3.323\,} Γ ( 4 ) = 3 ! = 6 {\displaystyle \Gamma (4)\,=3!=6\,}
ガンマ関数の対数微分
ψ ( z ) = d d z log Γ ( z ) {\displaystyle \psi (z)={\frac {d}{dz}}\log \Gamma (z)} をディガンマ関数 (Digamma function)と呼ぶ。同様の対数微分を繰り返した関数
ψ ( n ) ( z ) = d n + 1 d z n + 1 log Γ ( z ) {\displaystyle \psi ^{(n)}(z)={\frac {d^{n+1}}{dz^{n+1}}}\log \Gamma (z)} を、ポリガンマ関数 (Polygamma function)と呼ぶ。
^ a b E. T. Whittaker and G. N. Watson (1927), Chapter XII, §12.1 ^ Wolfram mathworld: Gamma Function ^ Springer Online Reference Works: Gamma-function ^ Schmelzer & Trefethen (2007), Computing the Gamma function using contour integrals and rational approximations ^ a b 小松 (2004)、第2章 ^ Otto Ludwig Hölder, "Über die Eigenschaft der Gammafunction keiner algebraischen Differentialgleichung zu genügen," Math. Ann. , 28 , (1887) pp. 1–13. doi :10.1007/BF02430507 ^ Eliakim Hastings Moore, "Concerning transcendentally transcendental functions," Math. Ann. , 48 (1897), pp. 49–74. doi :10.1007/BF01446334 ^ A. Ostrowski, "Neuer Beweis der Hölderschen Satzes, dass die Gammafunktion keiner algebraischen Differntialgleichung genügt." Math. Ann. 79 (1919), pp. 286–288. doi :10.1007/BF01458212 ^ A. Ostrowski, "Zum Hölderschen Satz über Γ(x). Math. Ann. 94 (1925), pp. 248–251. doi :10.1007/BF01208657 ^ E. W. Barnes, "The theory of the Gamma function," Messenger of Math. 29 (1900), pp. 64–128. ^ F. Hausdorff, "Zum Hölderschen Satz über Γ(x)," Math. Ann. 94 (1925), pp. 244–247. doi :10.1007/BF01208656 



 French
French Deutsch
Deutsch









![{\displaystyle {\begin{aligned}\Gamma (z+1)&=\int _{0}^{\infty }e^{-t}t^{z}\,{\rm {d}}t\\&={\Bigl [}-e^{-t}t^{z}{\Bigr ]}_{0}^{\infty }+z\int _{0}^{\infty }e^{-t}t^{z-1}\,{\rm {d}}t\\&=z\Gamma (z)\qquad \left(\because {\Bigl [}-e^{-t}t^{z}{\Bigr ]}_{0}^{\infty }=0\right)\!,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11ee46dd4999406a1d95971915506839ecb211b2)

![{\displaystyle {\begin{aligned}\Gamma (1)&=\int _{0}^{\infty }e^{-t}\,{\rm {d}}t={\Bigl [}-e^{-t}{\Bigr ]}_{0}^{\infty }=\lim _{t\to \infty }\!\left(-e^{-t}+1\right)\\&=1,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9960a09a00ac0836df78febf40ba717a29cbbd77)












![{\displaystyle g_{0}(z)=\int _{0}^{1}{u^{z-1}}{\rm {d}}u=\left[{\frac {u^{z}}{z}}\right]_{u=0}^{1}={\frac {1}{z}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6a50b83c5f0b1fc1d74e5920340ea3198c60811)
















































![{\displaystyle {\begin{aligned}f(z+1)&={\frac {n^{nz-1/2}n^{n}\left[\prod _{k=0}^{n-1}\left(z+{\frac {k}{n}}\right)\Gamma {\left(z+{\frac {k}{n}}\right)}\right]}{(2\pi )^{(n-1)/2}\left[\prod _{k=0}^{n-1}(nz+k)\right]\Gamma (nz)}}\\&={\frac {n^{nz-1/2}\left[\prod _{k=0}^{n-1}\left(nz+k\right)\right]\prod _{k=0}^{n-1}\Gamma {\left(z+{\frac {k}{n}}\right)}}{(2\pi )^{(n-1)/2}\left[\prod _{k=0}^{n-1}(nz+k)\right]\Gamma (nz)}}\\&=f(z)\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8795bf1f2eac74b87d83d5aba87359d3afa49e25)


![{\displaystyle {\begin{aligned}\lim _{\Re {z}\to +\infty }f(z)&=\lim _{\Re {z}\to +\infty }{\frac {n^{nz-1/2}\left[\prod _{k=0}^{n-1}{{\sqrt {\frac {2{\pi }}{z+k/n}}}\left({\frac {z+k/n}{e}}\right)^{z+k/n}}\right]}{(2\pi )^{(n-1)/2}{\sqrt {\frac {2{\pi }}{nz}}}\left({\frac {nz}{e}}\right)^{nz}}}\\&=\lim _{\Re {z}\to +\infty }z^{1/2}\left[\prod _{k=0}^{n-1}z^{k/n-1/2}(1+k/nz)^{z+k/n-1/2}e^{-k/n}\right]\\&=\lim _{\Re {z}\to +\infty }z^{1/2}\left[\prod _{k=0}^{n-1}z^{k/n-1/2}e^{k/n}e^{-k/n}\right]\\&=1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a686140ff4a6407eed31b51420c4a82f40c2ac8)
















