シャノン・ファノ符号化
シャノン・ファノ符号化(シャノン・ファノふごうか)とは、1948年にクロード・シャノンとロベルト・ファノによって考案された可逆圧縮の方法である。
概要
[編集]記号の(推定もしくは実際の)出現確率に基づく接頭符号を使用している。同じ接頭符号でも、常に最短の符号長を表すことができ、コンパクト符号と呼ばれるハフマン符号に比べ、シャノン・ファノ符号化は最適化されていない。しかし、ハフマン符号とは違い、全ての記号のコード長が理論上の理想の1ビット以内にあることは保証されている。
この符号化法は1948年のシャノンの情報理論の記事『通信の数学的理論』の中で提案された。この符号化法はファノによるもので、ファノは後にテクニカルレポートとして発表している[1]。
シャノン・ファノ符号化は、シャノンの情報源符号化定理の証明のために用いられたシャノン符号化や、算術符号の先駆者であるシャノン・ファノ・イライアス符号化(またはイライアス符号化)とは異なる。
符号化の原理
[編集]- 記号を出現確率の高い物から低い物の順に並べ替える。
- それぞれの集合の確率の合計ができるだけ等しくなるようなところで二分割する。
- 分割した片方の集合に"0"、もう片方の集合に"1"を割り当て、符号の1桁目とする。
- 分割して出来た2つの集合をそれぞれ更に二分割し、同様に0と1を割り当てる。
この操作を、各集合に含まれる記号が1つになるまで行うと、それぞれの記号の符号が得られる。
このアルゴリズムは、かなり効率の良い可変長の符号を生成する。分割によって作られた2つの集号は、実際にほぼ等しい出現確率がある。それらを識別するのに用いられる1ビットの情報は、最も効率的に使われる。 残念なことに、シャノン・ファノ符号化は常に最短の符号を表すとは限らない。{0.35, 0.17, 0.17, 0.16, 0.15}という出現確率の集合からは、シャノン・ファノ符号化では最適化されていない符号が生成される。
この理由から、シャノン・ファノ符号化が用いられることは少ない。多くの場合はハフマン符号、あるいは算術符号やRange Coderが用いられる。
例
[編集]
5種類の記号が以下の個数出現するデータを考える。
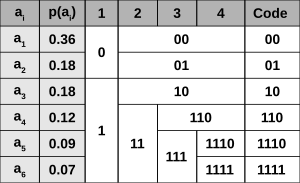
記号 A B C D E 個数 15 7 6 6 5 出現確率 0.38461538 0.17948718 0.15384615 0.15384615 0.12820513
記号は左から右に出現個数の順に並べてある(右図のaの状態)。ここで、BとCの間で分割をすると、左の集合は合計22個、右の集合は合計17個となる。この分割が、2つの集合の合計個数の差が最も小さくなる分割である。ここで、左の集合に含まれる記号A,Bに"0"、右の集合に含まれる記号C,D,Eに"1"を与え、それぞれの符号の1桁目とする(右図のbの状態)。
右の集合は含まれる記号が2つしかないので、AとBの間で分割して、アルゴリズムは終了となる。Aに"0"、Bに"1"を与えて符号の2桁目とし、Aの符号は"00"、Bの符号は"01"となる。左の集合はCとDの間で分割して同様に"0"、"1"を与える(右図のcの状態)。さらにD,Eの集合はDとEに分割される(右図のdの状態)。
上記の4回の分割手順により、符号木が生成される。最も頻度の高い3つの記号は全て2ビットの符号が割り当てられ、頻度の低い2つの記号には3ビットの符号が割り当てられた。
記号 A B C D E 符号 00 01 10 110 111
1文字あたりの平均符号長は
となる。
脚注
[編集]参考文献
[編集]- Shannon, C.E. (July 1948). “A Mathematical Theory of Communication”. Bell System Technical Journal 27: 379–423.
- Fano, R.M. (1949). “The transmission of information”. Technical Report No. 65 (アメリカ合衆国マサチューセッツ州ケンブリッジ: MIT電子工学研究所).


 French
French Deutsch
Deutsch
